Chapter 14, Problem 54CCSR

Solution

a.

To write: The system of inequalities.

  $\begin{array}{c}7x+11y\le 200\\ 3x+4y\le 80\\ x\ge 0\\ y\ge 0\end{array}$

Given:

A regular doghouse requires 7 hours to build and 3 hours to paint.

A deluxe doghouse requires 11 hours to build and 4 hours to paint.

The company employs 5 builders and 2 painters.

Each employee can work a maximum of 40 hours.

Calculation:

Let $x$ be the number of regular doghouses, and $y$ be the number of deluxe doghouses.

Since there are 5 builders and each can work for a maximum of 40 hours, therefore the total building hours available is

  $40\times 5=200$ hours.

Since there are 2 painters and each can work for a maximum of 40 hours, therefore the total painting hours available is

  $40\times 2=80$ hours.

The number of hours required to build $x$ regular doghouses is $7x$ and the number of hours required to build $y$ deluxe doghouses is $11y$ .

Therefore, the building hour’s inequality is

  $7x+11y\le 200$

The number of hours required to paint $x$ regular doghouses is $3x$ and the number of hours required to paint $y$ deluxe doghouses is $4y$ .

Therefore, the painting hour’s inequality is

  $3x+4y\le 80$

Since the number of doghouses cannot be negative, therefore

  $x\ge 0,y\ge 0$

Hence, the system of inequalities is,

  $\begin{array}{c}7x+11y\le 200\\ 3x+4y\le 80\\ x\ge 0\\ y\ge 0\end{array}$

b.

To graph: Solution set of the system of inequalities in part (a).

  

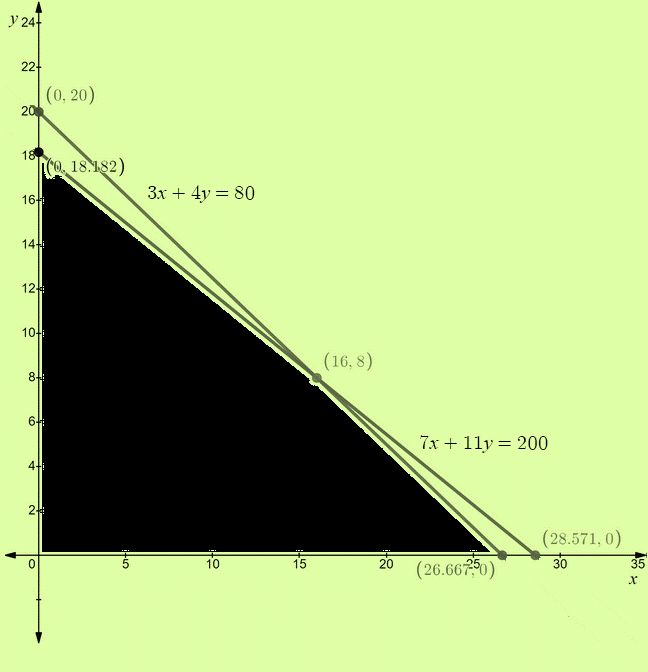
Given:

  $\begin{array}{c}7x+11y\le 200\\ 3x+4y\le 80\\ x\ge 0\\ y\ge 0\end{array}$

Calculation:

The graph of the system of inequalities is,

  

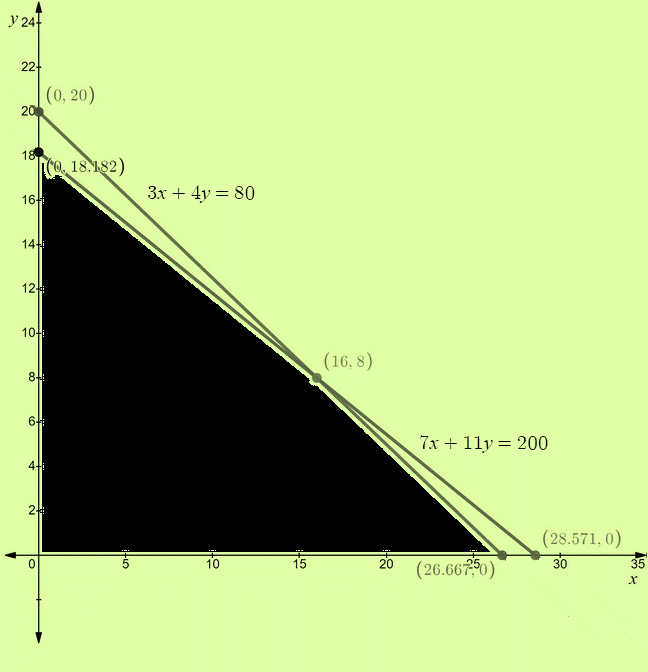
The shaded region is the solution set of the system of inequalities.

c.

To find: the number of doghouses must be built, painted to maximize sales.

Approximately 18 deluxe doghouses must be built and painted to maximize the sales.

Given:

A regular doghouse can be sold for $100, and the deluxe doghouse can be sold for $200.

Calculation:

The amount received from selling $x$ regular doghouses and $y$ deluxe doghouses is,

  $A=100x+200y$

The corner points of the solution set are $\left(0,18.182\right),\left(16,8\right),\left(26.667,0\right)$ .

Now at $\left(0,18.182\right)$ ,

  $\begin{array}{c}A=100\left(0\right)+200\left(18.182\right)\\ =\$3636.4\end{array}$

At $\left(16,8\right)$ ,

  $\begin{array}{c}A=100\left(16\right)+200\left(8\right)\\ =\$3200\end{array}$

At $\left(26.667,0\right)$ ,

  $\begin{array}{c}A=100\left(26.667\right)+200\left(0\right)\\ =\$2666.7\end{array}$

Clearly, the maximum sales is $3636.4 and it occurs at the point $\left(0,18.182\right)$ .

Hence, approximately 18 deluxe doghouses must be built and painted to maximize the sales.