Holt Mcdougal Larson Pre-algebra: Student Edition 2012
Holt Mcdougal Larson Pre-algebra: Student Edition 2012
1st Edition
ISBN: 9780547587776
Author: HOLT MCDOUGAL
Publisher: HOLT MCDOUGAL
bartleby

Concept explainers

Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 …
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experime…
bartleby

Videos

Question
Book Icon
Chapter 1.4, Problem 51E

a.

To determine

To write an integer to represent the elevation provided in the table.

a.

Expert Solution
Check Mark

Answer to Problem 51E

The table is obtained as:

    SiteElevation relative to sea level
    Helike, Greece3 meters below =−3
    Heraklion, Egypt8 meters below =−8
    Port Royal, Jamaica12 meters below =−12
    Unnamed city, Bay of Bengal 37 meters below =−37

Explanation of Solution

Given information:

The table provided in the question,

    SiteElevation relative to sea level
    Helike, Greece3 meters below
    Heraklion, Egypt8 meters below
    Port Royal, Jamaica12 meters below
    Unnamed city, Bay of Bengal 37 meters below

Calculation:

From the table, it can be observed that the elevation relative to sea level is below. So, if elevation relative to sea level is below, use negative sign for it and for above sea level, positive sign is used.

Hence, writing an integer to represent the elevation provided in the table is obtained as:

    SiteElevation relative to sea level
    Helike, Greece3 meters below =−3
    Heraklion, Egypt8 meters below =−8
    Port Royal, Jamaica12 meters below =−12
    Unnamed city, Bay of Bengal 37 meters below =−37

b.

To determine

To graph the integers on number line.

b.

Expert Solution
Check Mark

Answer to Problem 51E

Explanation of Solution

Given information:

The table provided in the question,

    SiteElevation relative to sea level
    Helike, Greece3 meters below
    Heraklion, Egypt8 meters below
    Port Royal, Jamaica12 meters below
    Unnamed city, Bay of Bengal 37 meters below

Graph:

From the above table, it can be observed that the integers which represent the elevation relative to sea level are −3,−8,−12,−37

Graph the integers on the number line and the graph is obtained as:

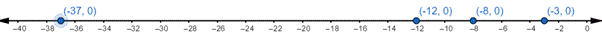
Holt Mcdougal Larson Pre-algebra: Student Edition 2012, Chapter 1.4, Problem 51E , additional homework tip 1

c.

To determine

To identify the site whose deepest point is farthest from the sea level.

c.

Expert Solution
Check Mark

Answer to Problem 51E

Unnamed city, Bay of Bengal is the site which is deepest from the sea level.

Explanation of Solution

Given information:

The table provided in the question,

    SiteElevation relative to sea level
    Helike, Greece3 meters below
    Heraklion, Egypt8 meters below
    Port Royal, Jamaica12 meters below
    Unnamed city, Bay of Bengal 37 meters below

From the above table, it can be observed that the integers which represent the elevation relative to sea level are −3,−8,−12,−37

The number line is obtained as:

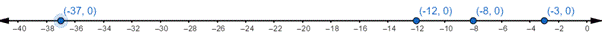
Holt Mcdougal Larson Pre-algebra: Student Edition 2012, Chapter 1.4, Problem 51E , additional homework tip 2

From the above number line, it can be observed that −37 is the least integer among all the integer.

Hence,

Unnamed city, Bay of Bengal is the site which is deepest from the sea level.

d.

To determine

To identify the site whose deepest point is farthest from the sea level.

d.

Expert Solution
Check Mark

Answer to Problem 51E

Polonia is closer to the sea-level than the deepest point of the ruins at Helike, Greece.

Explanation of Solution

Given information:

The table provided in the question,

    SiteElevation relative to sea level
    Helike, Greece3 meters below
    Heraklion, Egypt8 meters below
    Port Royal, Jamaica12 meters below
    Unnamed city, Bay of Bengal 37 meters below

1 meter above sea-level can be represent by the integer +1 .

Hence,

Polonia is closer to the sea-level than the deepest point of the ruins at Helike, Greece because +1 is closer to 0 than −3 on the number line.

Previous
Chapter 1.4, Problem 50E
Next
Chapter 1.4, Problem 52E

Chapter 1 Solutions

Holt Mcdougal Larson Pre-algebra: Student Edition 2012

Ch. 1.1 - Prob. 1CCh. 1.1 - Prob. 2CCh. 1.1 - Prob. 3CCh. 1.1 - Prob. 4CCh. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6E
Ch. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10ECh. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 17ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.1 - Prob. 64ECh. 1.1 - Prob. 65ECh. 1.1 - Prob. 66ECh. 1.1 - Prob. 67ECh. 1.2 - Prob. 1CCh. 1.2 - Prob. 2CCh. 1.2 - Prob. 3CCh. 1.2 - Prob. 4CCh. 1.2 - Prob. 5CCh. 1.2 - Prob. 6CCh. 1.2 - Prob. 7CCh. 1.2 - Prob. 8CCh. 1.2 - Prob. 9CCh. 1.2 - Prob. 10CCh. 1.2 - Prob. 11CCh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.3 - Prob. 1CCh. 1.3 - Prob. 2CCh. 1.3 - Prob. 3CCh. 1.3 - Prob. 4CCh. 1.3 - Prob. 5CCh. 1.3 - Prob. 6CCh. 1.3 - Prob. 7CCh. 1.3 - Prob. 8CCh. 1.3 - Prob. 9CCh. 1.3 - Prob. 10CCh. 1.3 - Prob. 11CCh. 1.3 - Prob. 12CCh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.4 - Prob. 1CCh. 1.4 - Prob. 2CCh. 1.4 - Prob. 3CCh. 1.4 - Prob. 4CCh. 1.4 - Prob. 5CCh. 1.4 - Prob. 6CCh. 1.4 - Prob. 7CCh. 1.4 - Prob. 8CCh. 1.4 - Prob. 9CCh. 1.4 - Prob. 1ECh. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Prob. 69ECh. 1.4 - Prob. 70ECh. 1.4 - Prob. 71ECh. 1.4 - Prob. 72ECh. 1.4 - Prob. 73ECh. 1.4 - Prob. 74ECh. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.5 - Prob. 1CCh. 1.5 - Prob. 2CCh. 1.5 - Prob. 3CCh. 1.5 - Prob. 4CCh. 1.5 - Prob. 5CCh. 1.5 - Prob. 6CCh. 1.5 - Prob. 7CCh. 1.5 - Prob. 8CCh. 1.5 - Prob. 9CCh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.5 - Prob. 63ECh. 1.5 - Prob. 64ECh. 1.5 - Prob. 65ECh. 1.5 - Prob. 66ECh. 1.5 - Prob. 67ECh. 1.5 - Prob. 68ECh. 1.5 - Prob. 69ECh. 1.6 - Prob. 1CCh. 1.6 - Prob. 2CCh. 1.6 - Prob. 3CCh. 1.6 - Prob. 4CCh. 1.6 - Prob. 5CCh. 1.6 - Prob. 6CCh. 1.6 - Prob. 7CCh. 1.6 - Prob. 8CCh. 1.6 - Prob. 9CCh. 1.6 - Prob. 10CCh. 1.6 - Prob. 11CCh. 1.6 - Prob. 12CCh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.7 - Prob. 1CCh. 1.7 - Prob. 2CCh. 1.7 - Prob. 3CCh. 1.7 - Prob. 4CCh. 1.7 - Prob. 5CCh. 1.7 - Prob. 6CCh. 1.7 - Prob. 7CCh. 1.7 - Prob. 8CCh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - Prob. 36ECh. 1.7 - Prob. 37ECh. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1.7 - Prob. 52ECh. 1.8 - Prob. 1CCh. 1.8 - Prob. 2CCh. 1.8 - Prob. 3CCh. 1.8 - Prob. 4CCh. 1.8 - Prob. 5CCh. 1.8 - Prob. 6CCh. 1.8 - Prob. 7CCh. 1.8 - Prob. 1ECh. 1.8 - Prob. 2ECh. 1.8 - Prob. 3ECh. 1.8 - Prob. 4ECh. 1.8 - Prob. 5ECh. 1.8 - Prob. 6ECh. 1.8 - Prob. 7ECh. 1.8 - Prob. 8ECh. 1.8 - Prob. 9ECh. 1.8 - Prob. 10ECh. 1.8 - Prob. 11ECh. 1.8 - Prob. 12ECh. 1.8 - Prob. 13ECh. 1.8 - Prob. 14ECh. 1.8 - Prob. 15ECh. 1.8 - Prob. 16ECh. 1.8 - Prob. 17ECh. 1.8 - Prob. 18ECh. 1.8 - Prob. 19ECh. 1.8 - Prob. 20ECh. 1.8 - Prob. 21ECh. 1.8 - Prob. 22ECh. 1.8 - Prob. 23ECh. 1.8 - Prob. 24ECh. 1.8 - Prob. 25ECh. 1.8 - Prob. 26ECh. 1.8 - Prob. 27ECh. 1.8 - Prob. 28ECh. 1.8 - Prob. 29ECh. 1.8 - Prob. 30ECh. 1.8 - Prob. 31ECh. 1.8 - Prob. 32ECh. 1.8 - Prob. 33ECh. 1.8 - Prob. 34ECh. 1.8 - Prob. 35ECh. 1.8 - Prob. 36ECh. 1.8 - Prob. 37ECh. 1.8 - Prob. 38ECh. 1.8 - Prob. 39ECh. 1.8 - Prob. 40ECh. 1.8 - Prob. 41ECh. 1.8 - Prob. 42ECh. 1.8 - Prob. 43ECh. 1.8 - Prob. 44ECh. 1 - Prob. 1PSQCh. 1 - Prob. 2PSQCh. 1 - Prob. 3PSQCh. 1 - Prob. 4PSQCh. 1 - Prob. 5PSQCh. 1 - Prob. 6PSQCh. 1 - Prob. 7PSQCh. 1 - Prob. 8PSQCh. 1 - Prob. 9PSQCh. 1 - Prob. 10PSQCh. 1 - Prob. 1MCQCh. 1 - Prob. 2MCQCh. 1 - Prob. 3MCQCh. 1 - Prob. 4MCQCh. 1 - Prob. 5MCQCh. 1 - Prob. 6MCQCh. 1 - Prob. 7MCQCh. 1 - Prob. 8MCQCh. 1 - Prob. 9MCQCh. 1 - Prob. 10MCQCh. 1 - Prob. 11MCQCh. 1 - Prob. 12MCQCh. 1 - Prob. 13MCQCh. 1 - Prob. 14MCQCh. 1 - Prob. 15MCQCh. 1 - Prob. 16MCQCh. 1 - Prob. 17MCQCh. 1 - Prob. 18MCQCh. 1 - Prob. 19MCQCh. 1 - Prob. 20MCQCh. 1 - Prob. 21MCQCh. 1 - Prob. 22MCQCh. 1 - Prob. 23MCQCh. 1 - Prob. 1CRCh. 1 - Prob. 2CRCh. 1 - Prob. 3CRCh. 1 - Prob. 4CRCh. 1 - Prob. 5CRCh. 1 - Prob. 6CRCh. 1 - Prob. 7CRCh. 1 - Prob. 8CRCh. 1 - Prob. 9CRCh. 1 - Prob. 10CRCh. 1 - Prob. 11CRCh. 1 - Prob. 12CRCh. 1 - Prob. 13CRCh. 1 - Prob. 14CRCh. 1 - Prob. 15CRCh. 1 - Prob. 16CRCh. 1 - Prob. 17CRCh. 1 - Prob. 18CRCh. 1 - Prob. 19CRCh. 1 - Prob. 20CRCh. 1 - Prob. 21CRCh. 1 - Prob. 22CRCh. 1 - Prob. 23CRCh. 1 - Prob. 24CRCh. 1 - Prob. 25CRCh. 1 - Prob. 26CRCh. 1 - Prob. 27CRCh. 1 - Prob. 28CRCh. 1 - Prob. 29CRCh. 1 - Prob. 30CRCh. 1 - Prob. 31CRCh. 1 - Prob. 32CRCh. 1 - Prob. 33CRCh. 1 - Prob. 34CRCh. 1 - Prob. 35CRCh. 1 - Prob. 36CRCh. 1 - Prob. 37CRCh. 1 - Prob. 38CRCh. 1 - Prob. 39CRCh. 1 - Prob. 40CRCh. 1 - Prob. 41CRCh. 1 - Prob. 42CRCh. 1 - Prob. 43CRCh. 1 - Prob. 44CRCh. 1 - Prob. 45CRCh. 1 - Prob. 46CRCh. 1 - Prob. 47CRCh. 1 - Prob. 48CRCh. 1 - Prob. 49CRCh. 1 - Prob. 50CRCh. 1 - Prob. 51CRCh. 1 - Prob. 52CRCh. 1 - Prob. 53CRCh. 1 - Prob. 54CRCh. 1 - Prob. 55CRCh. 1 - Prob. 56CRCh. 1 - Prob. 57CRCh. 1 - Prob. 58CRCh. 1 - Prob. 59CRCh. 1 - Prob. 60CRCh. 1 - Prob. 61CRCh. 1 - Prob. 62CRCh. 1 - Prob. 63CRCh. 1 - Prob. 64CRCh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CTCh. 1 - Prob. 21CTCh. 1 - Prob. 22CTCh. 1 - Prob. 23CTCh. 1 - Prob. 24CTCh. 1 - Prob. 25CTCh. 1 - Prob. 26CTCh. 1 - Prob. 27CTCh. 1 - Prob. 28CTCh. 1 - Prob. 29CTCh. 1 - Prob. 30CTCh. 1 - Prob. 31CTCh. 1 - Prob. 32CTCh. 1 - Prob. 33CTCh. 1 - Prob. 34CTCh. 1 - Prob. 35CTCh. 1 - Prob. 36CTCh. 1 - Prob. 37CTCh. 1 - Prob. 38CTCh. 1 - Prob. 39CTCh. 1 - Prob. 1CSTCh. 1 - Prob. 2CSTCh. 1 - Prob. 3CSTCh. 1 - Prob. 4CSTCh. 1 - Prob. 5CSTCh. 1 - Prob. 6CSTCh. 1 - Prob. 7CSTCh. 1 - Prob. 8CSTCh. 1 - Prob. 9CSTCh. 1 - Prob. 10CSTCh. 1 - Prob. 11CSTCh. 1 - Prob. 12CSTCh. 1 - Prob. 13CSTCh. 1 - Prob. 1PSPCh. 1 - Prob. 2PSPCh. 1 - Prob. 3PSPCh. 1 - Prob. 4PSPCh. 1 - Prob. 5PSPCh. 1 - Prob. 6PSPCh. 1 - Prob. 7PSP

Additional Math Textbook Solutions

Find more solutions based on key concepts
4. You construct a 95% confidence interval for a population mean using a random sample. The confidence interval...

Elementary Statistics: Picturing the World (7th Edition)

Explain the meaning of the term “statistically significant difference” in statistics terminology.

Intro Stats, Books a la Carte Edition (5th Edition)

Which of the sequences {an} in Exercises 31–100 converge, and which diverge? Find the limit of each convergent ...

University Calculus: Early Transcendentals (4th Edition)

Growing sandpile Sand falls from an overhead bin and accumulates in a conical pile with a radius that is always...

Calculus: Early Transcendentals (2nd Edition)

In Exercises 11-20, express each decimal as a percent. 11. 0.59

Thinking Mathematically (6th Edition)

Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...

Algebra and Trigonometry (6th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY