Chapter 14, Problem 46E

To determine

To find:

• The range of the given projectile equations.

• The graph of the projectile at suitable x values.

• The graph of the height versus time.

• The range of the given projectile equations.

Answer to Problem 46E

Solution:

• The required range is $0.35$

• The required graph is stated as follows.

• The required graph is stated as follows.

• The required apex is $0.1$.

Explanation of Solution

• The range of the given projectile equations.

The given equations are,

$\begin{array}{rll}\text{x}& =& {\text{v}}_{\text{0}}\cos \left({\theta }_0\right)\text{t}\\ \text{y}& =& {\text{v}}_{\text{0}}\sin \left({\theta }_0\right)\text{t}-\frac{1}{2}{\text{gt}}^{\text{2}}\end{array}$

The formula to calculate the range is,

$\text{range}=\frac{{\text{v}}_{\text{0}}{}^2\sin \left(2{\theta }_0\right)}{\text{g}}$

Here, ${\text{v}}_{\text{0}}$ is the initial velocity, ${\theta }_0$ is the angle of departure, $\text{g}$ is the acceleration due to gravity and $\text{t}$ is the time.

Let ${\text{v}}_{\text{0}}$ be $2\text{m/s}$, ${\theta }_0$ be $30°$, $\text{t}$ be $1\sec$ and $\text{g}$ be $9.81\text{m/s}$.

Substitute $2\text{m/s}$ for ${\text{v}}_{\text{0}}$, $30°$ for ${\theta }_0$, $1\sec$ for $\text{t}$ and $9.81\text{m/s}$ for $\text{g}$ in the above equation.

$\begin{array}{rll}\text{range}& =& \frac{{\text{v}}_{\text{0}}{}^2\sin \left(2{\theta }_0\right)}{\text{g}}\\ & =& \frac{{\text{2}}^2\sin \left(2\times 30°\right)}{9.81}\\ & =& 0.35\end{array}$

MATLAB Code:

t = 0:0.001:2;

v0 = 2;

g = 9.81;

theta = 30;

x = v0.*cosd(theta).*t;

y = v0.*sind(theta).*t -0.5.*g.*t.*t;

range = v0.^2.*sind(2*theta)/g

Save the MATLAB function with name chapter14_54793_14_46_1E.m in the current folder. Execute the function by typing the function name at the command window to generate output.

Result:

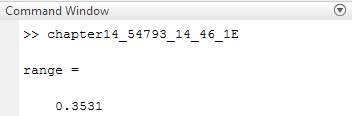
Therefore, the result is stated above.

• The graph of the projectile at suitable x values.

MATLAB Code:

t = 0:0.001:2;

v0 = 2;

g = 9.81;

theta = 30;

x = v0.*cosd(theta).*t;

y = v0.*sind(theta).*t -0.5.*g.*t.*t;

plot(t, x)

title('Position(x) vs Time(t)')

Save the MATLAB function with name chapter14_54793_14_46_2E.m in the current folder. Execute the function by typing the function name at the command window to generate output.

Result:

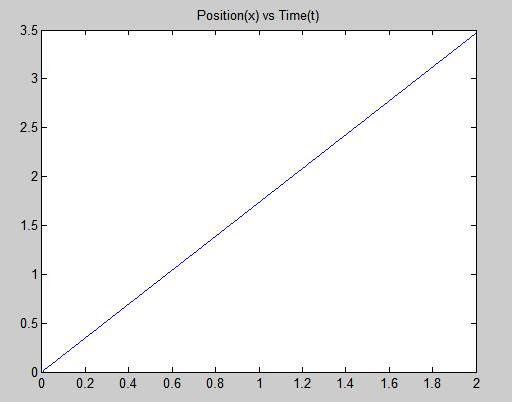
Therefore, the result is stated above.

• The graph of the height versus time.

MATLAB Code:

t = 0:0.001:2;

v0 = 2;

g = 9.81;

theta = 30;

x = v0.*cosd(theta).*t;

y = v0.*sind(theta).*t -0.5.*g.*t.*t;

plot(t, y)

title('Height(y) vs Time(t)')

Save the MATLAB function with name chapter14_54793_14_46_3E.m in the current folder. Execute the function by typing the function name at the command window to generate output.

Result:

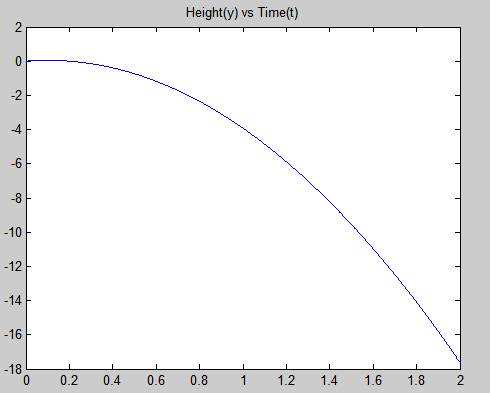
Therefore, the result is stated above.

• The range of the given projectile equations.

The given equations are,

$\begin{array}{rll}\text{x}& =& {\text{v}}_{\text{0}}\cos \left({\theta }_0\right)\text{t}\\ \text{y}& =& {\text{v}}_{\text{0}}\sin \left({\theta }_0\right)\text{t}-\frac{1}{2}{\text{gt}}^{\text{2}}\end{array}$

The formula to calculate the maximum time, ${\text{t}}_{\max }$ is,

${\text{t}}_{\max }=\frac{{\text{v}}_{\text{0}}\sin \left({\theta }_0\right)}{\text{g}}$

Here, ${\text{v}}_{\text{0}}$ is the initial velocity, ${\theta }_0$ is the angle of departure, $\text{g}$ is the acceleration due to gravity and $\text{t}$ is the time.

Let ${\text{v}}_{\text{0}}$ be $2\text{m/s}$, ${\theta }_0$ be $30°$, $\text{t}$ be $1\sec$ and $\text{g}$ be $9.81\text{m/s}$.

Substitute $2\text{m/s}$ for ${\text{v}}_{\text{0}}$, $30°$ for ${\theta }_0$, and $9.81\text{m/s}$ for $\text{g}$ in the above equation.

$\begin{array}{rll}{\text{t}}_{\max }& =& \frac{{\text{v}}_{\text{0}}\sin \left({\theta }_0\right)}{\text{g}}\\ & =& \frac{\text{2}\sin \left(30°\right)}{\text{9}\text{.81}}\\ & =& 0.10\sec \end{array}$

MATLAB Code:

t = 0:0.001:2;

v0 = 2;

g = 9.81;

theta = 30;

x = v0.*cosd(theta).*t;

y = v0.*sind(theta).*t -0.5.*g.*t.*t;

apex_time = v0*sind(theta)/g;

fprintf('The apex is %.1f\n', apex_time)

Save the MATLAB function with name chapter14_54793_14_46_4E.m in the current folder. Execute the function by typing the function name at the command window to generate output.

Result:

Therefore, the required apex is $0.1$.