Chapter 1.4, Problem 1SP

Consider the graph in Figure 1.42 of the function $y=\sin x+\cos x$ . Describe its overall shape. Is it periodic? How do you know?

  

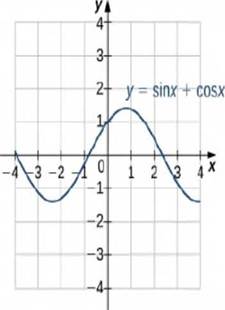
Figure 1.42 The graph of $y=\sin x+\cos x$ .

Using a graphing calculator or other graphing device, estimate the x - and y -values of the maximum point for the graph (the first such point where x >0). It may be helpful to express the x -value as a multiple of $\pi$ .