
Concept explainers
To calculate: The total interest amount and future value of annuity in the following table using Excel worksheet,
Annuity payment |
Annual Rate |
Annual interest |
Years |
Type of annuity |
Future value of annuity |
Total interest |
$1400 |
3% |
Compounded annually |
5 |
Ordinary |
Answer to Problem 1ES
Solution:
The total interest amount and future value of annuity in the following table is,
Annuity payment |
Annual Rate |
Annual interest |
Years |
Type of annuity |
Future value of annuity |
Total interest |
$1400 |
3% |
Compounded annually |
5 |
Ordinary |
$7432.790 |
$432.790 |
Explanation of Solution
Given Information:
The provided table is,
Annuity payment |
Annual Rate |
Annual interest |
Years |
Type of annuity |
Future value of annuity |
Total interest |
$1400 |
3% |
Compounded annually |
5 |
Ordinary |
Formula used:
Sinking fund payment
Calculation:
Consider the table,
Annuity payment |
Annual Rate |
Annual interest |
Years |
Type of annuity |
Future value of annuity |
Total interest |
$1400 |
3% |
Compounded annually |
5 |
Ordinary |
To find the Future value of annuity follow the steps,
Step 1: Open an Excel worksheet.
Step 2: Write the annuity payment $1400 in the cell B3.
Step 3: Write the annual rate of interest 3% in the cell B4.
Step 4: As the annual interest compounded annual hence write the number of period as 1 in the cell B5.
Step 5: Write the number of years 5 in the cell B6.
Step 6: To calculate the total number of period write “
Step 7: To calculate the periodic interest rate write “
Step 8: To calculate the Sinking fund payment write “
Step 9: To calculate the total payment write “
Step 10: To calculate the total interest write “
Therefore,
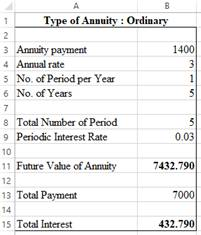
Therefore the completed table is,
Annuity payment |
Annual Rate |
Annual interest |
Years |
Type of annuity |
Future value of annuity |
Total interest |
$1400 |
3% |
Compounded annually |
5 |
Ordinary |
$7432.790 |
$432.790 |
Want to see more full solutions like this?
Chapter 14 Solutions
Business Math (11th Edition)
- a -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forwardWhen a tennis player serves, he gets two chances to serve in bounds. If he fails to do so twice, he loses the point. If he attempts to serve an ace, he serves in bounds with probability 3/8.If he serves a lob, he serves in bounds with probability 7/8. If he serves an ace in bounds, he wins the point with probability 2/3. With an in-bounds lob, he wins the point with probability 1/3. If the cost is '+1' for each point lost and '-1' for each point won, the problem is to determine the optimal serving strategy to minimize the (long-run)expected average cost per point. (Hint: Let state 0 denote point over,two serves to go on next point; and let state 1 denote one serve left. (1). Formulate this problem as a Markov decision process by identifying the states and decisions and then finding the Cik. (2). Draw the corresponding state action diagram. (3). List all possible (stationary deterministic) policies. (4). For each policy, find the transition matrix and write an expression for the…arrow_forward
- During each time period, a potential customer arrives at a restaurant with probability 1/2. If there are already two people at the restaurant (including the one being served), the potential customer leaves the restaurant immediately and never returns. However, if there is one person or less, he enters the restaurant and becomes an actual customer. The manager has two types of service configurations available. At the beginning of each period, a decision must be made on which configuration to use. If she uses her "slow" configuration at a cost of $3 and any customers are present during the period, one customer will be served and leave with probability 3/5. If she uses her "fast" configuration at a cost of $9 and any customers are present during the period, one customer will be served and leave with probability 4/5. The probability of more than one customer arriving or more than one customer being served in a period is zero. A profit of $50 is earned when a customer is served. The manager…arrow_forwardEvery Saturday night a man plays poker at his home with the same group of friends. If he provides refreshments for the group (at an expected cost of $14) on any given Saturday night, the group will begin the following Saturday night in a good mood with probability 7/8 and in a bad mood with probability 1/8. However, if he fail to provide refreshments, the group will begin the following Saturday night in a good mood with probability 1/8 and in a bad mood with probability 7/8 regardless of their mood this Saturday. Furthermore, if the group begins the night in a bad mood and then he fails to provide refreshments, the group will gang up on him so that he incurs expected poker losses of $75. Under other circumstances he averages no gain or loss on his poker play. The man wishes to find the policy regarding when to provide refreshments that will minimize his (long-run) expected average cost per week. (1). Formulate this problem as a Markov decision process by identifying the states and…arrow_forwardThis year Amanda decides to invest in two different no-load mutual funds: the G Fund or the L Mutual Fund. At the end of each year, she liquidates her holdings, takes her profits, and then reinvests. The yearly profits of the mutual funds depend on where the market stood at the end of the preceding year. Recently the market has been oscillating around level 2 from one year end to the next, according to the probabilities given in the following transition matrix : L1 L2 L3 L1 0.2 0.4 0.4 L2 0.1 0.4 0.5 L3 0.3 0.3 0.4 Each year that the market moves up (down) 1 level, the G Fund has profits (losses) of $20k, while the L Fund has profits (losses) of $10k. If the market moves up (down) 2 level in a year, the G Fund has profits (losses) of $50k, while the L Fund has profits (losses) of only $20k. If the market does not change, there is no profit or loss for either fund. Amanda wishes to determine her optimal investment policy in order to maximize her (long-run) expected average profit per…arrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





