Chapter 14, Problem 14.25E

(a)

To determine

The values of n and p.

Answer to Problem 14.25E

The value of n is 5 and value of p is 0.65.

Explanation of Solution

The given information is that the believer in the random walk theory of stock markets thinks that an index of stock prices has probability 0.65 of increasing in any year. X is the number of years among the next five years in which the index rises.

The binomial distribution formula is

$P\left(x\right)=\frac{n!}{\left(n-x\right)!x!}{p}^x{q}^{n-x}$

Where, n is the number of trials, x is the number of successes among n trials, p is the probability of successes, and q is the probability of failure.

As given that X is a binomial probability distribution, n is the total number of observations and p is the probability of success. As given that the probability of increasing in any year is 0.65, which shows probability of success so p is 0.65. Also given that X is the number of years among the next five years in which the index rises, which means the number of observation is 5 years so the value of n is 5.

Thus, the value of n is 5 and value of p is 0.65.

(b)

To determine

The possible values that X can take.

Answer to Problem 14.25E

The possible values that X can take are $S=\left\{0,1,2,3,4,5\right\}$.

Explanation of Solution

As given in the question that X denotes the number of years in which the index rises. As there are 5 total number of years, so the set of possible values that X can take are:

$S=\left\{0,1,2,3,4,5\right\}$

It is because the value of X could be 0 when there is no index rises in any year and 5 when index rises in all 5 years, similarly all other values are possible. So the possible values that X can take are $S=\left\{0,1,2,3,4,5\right\}$.

Thus, the possible values that X can take are $S=\left\{0,1,2,3,4,5\right\}$.

(c)

To determine

To find: The probability of each value of X.

Answer to Problem 14.25E

The probabilities of each value of X are 0.00525, 0.04875, 0.18115, 0.33642, 0.31239 and 0.11603 for values of X as 0, 1, 2, 3, 4, and 5 respectively.

Explanation of Solution

The binomial distribution formula is

$P\left(x\right)=\frac{n!}{\left(n-x\right)!x!}{p}^x{q}^{n-x}$

Where, n is the number of trials, x is the number of successes among n trials, p is the probability of successes, and q is the probability of failure.

As discussed in part (a) that the possible values that X can take are $S=\left\{0,1,2,3,4,5\right\}$. As given that X has a binomial distribution so probability calculated as:

$P\left(X=k\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}$

Where k denotes number of events occur which is all possible sets, n denotes total number of events which is 5, p denotes probability of success which is 0.65 and q denotes probability of fail which is 0.35. Now substitute these values and k as 0 in the binomial probability formula then:

$\begin{array}{c}P\left(X=0\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}\\ =\left(\frac{5!}{0!5!}\right)\times {(0.65)}^0\times {(0.35)}^5\\ =1\times 0.005252\\ =0.00525\end{array}$

So, the probability when X is equal to 0 is 0.00525. If k is 1 then the probability is:

$\begin{array}{c}P\left(X=1\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}\\ =\left(\frac{5!}{1!4!}\right)\times {(0.65)}^1\times {(0.35)}^4\\ =5\times 0.65\times 0.015\\ =0.04875\end{array}$

So, the probability when X is equal to 1 is 0.04875. If k is 2 then the probability is:

$\begin{array}{c}P\left(X=2\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}\\ =\left(\frac{5!}{2!3!}\right)\times {(0.65)}^2\times {(0.35)}^3\\ =10\times 0.4225\times 0.042875\\ =0.18115\end{array}$

So, the probability when X is equal to 2 is 0.18115. If k is 3 then the probability is:

$\begin{array}{c}P\left(X=3\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}\\ =\left(\frac{5!}{3!2!}\right)\times {(0.65)}^3\times {(0.35)}^2\\ =10\times 0.274625\times 0.1225\\ =0.33642\end{array}$

So, the probability when X is equal to 3 is 0.33642. If k is 4 then the probability is:

$\begin{array}{c}P\left(X=4\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}\\ =\left(\frac{5!}{4!1!}\right)\times {(0.65)}^4\times {(0.35)}^1\\ =5\times 0.17851\times 0.35\\ =0.31239\end{array}$

So, the probability when X is equal to 4 is 0.31239. If k is 5 then the probability is:

$\begin{array}{c}P\left(X=5\right)=\left(\frac{n!}{k!\left(n-k\right)!}\right)\times p^k\times q^{(n-k)}\\ =\left(\frac{5!}{5!0!}\right)\times {(0.65)}^5\times {(0.35)}^0\\ =1\times 0.116029\times 1\\ =0.11603\end{array}$

So, the probability when X is equal to 5 is 0.11603.

Software procedure:

Step-by-step procedure to obtain the probability histogram for the distribution of X using the MINITAB software:

• Choose Graph > Probability Distribution Plot choose View Single > Click OK.
• From Distribution, choose ‘Binomial’ distribution.
• Enter the Number of trials as 5 and Event probability as 0.65.
• Click OK.
• Output using the MINITAB software is given below:

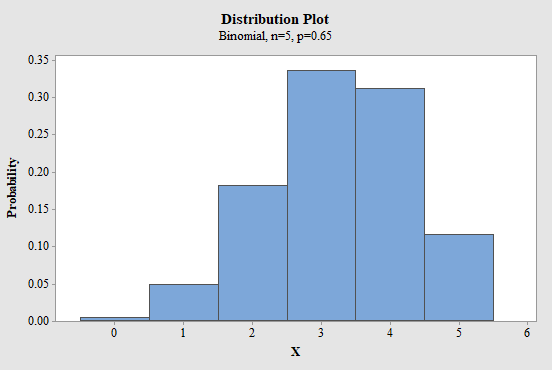
                                                                  Figure-1

Conclusion:

The probabilities of each value of X are 0.00525, 0.04875, 0.18115, 0.33642, 0.31239 and 0.11603 for values of X as 0, 1, 2, 3, 4, and 5 respectively.

(d)

To determine

To calculate: The mean and standard deviation of the distribution.

To show: The location of the mean on the histogram.

Answer to Problem 14.25E

The mean of X is 3.25 and standard deviation of X is 1.1375.

Explanation of Solution

The binomial distribution formula is

$P\left(x\right)=\frac{n!}{\left(n-x\right)!x!}{p}^x{q}^{n-x}$

Where, n is the number of trials, x is the number of successes among n trials, p is the probability of successes, and q is the probability of failure.

As given that X is a binomial probability distribution, so mean of X is calculated as:

$\mu =n\times p$

Where $\mu$ denotes mean number of years, n denotes total number of samples which is 5, p denotes probability of success which is 0.65, now substitute these values then:

$\begin{array}{c}\mu =n\times p\\ =5\times 0.65\\ =3.25\end{array}$

So, the mean of X is 3.25. Standard deviation of X is calculated as:

$\begin{array}{c}\sigma =\sqrt{n\times p\times \left(1-p\right)}\\ =\sqrt{\mu \times \left(1-p\right)}\end{array}$

Where $\mu$ denotes mean of X which is 3.25 as calculated in part (a), n denotes total number of samples, p denotes probability of success which is 0.65, now substitute these values then:

$\begin{array}{c}\sigma =\sqrt{n\times p\times \left(1-p\right)}\\ =\sqrt{\mu \times \left(1-p\right)}\\ =\sqrt{3.25\times 0.35}\\ =1.1375\end{array}$

So, the standard deviation of X is 1.1375. To show mean value on the histogram use the above histogram to show mean value of 3.25.

                                                                Figure-2

Conclusion:

The mean of X is 3.25 and standard deviation of X is 1.1375.