
The LRFD design load and the ASD design loads for the given connection members.
Answer to Problem 14.1PFS
Explanation of Solution
Given:
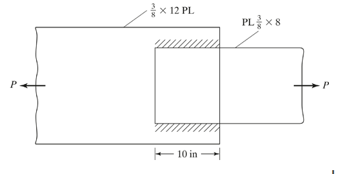
Calculation:
The ultimate load by LRFD is
The factored moment is
The factored shear force is
Refer Table 3-2 in the AISC steel construction manual.
Try
The required moment of inertia is
Refer Table 3-3 in the AISC steel construction manual.
Try
Hence, it’s safe.
The ultimate load by ASD is
The factored moment is
The factored shear force is
Refer Table 3-2 in the AISC steel construction manual.
Try
The required moment of inertia is
Refer Table 3-3 in the AISC steel construction manual.
Try
By taking from the minimum values we obtained we get the allowable and safe loads.
Conclusion:
Therefore, the required loads by LRFD and ASD are
Want to see more full solutions like this?
Chapter 14 Solutions
Structural Steel Design (6th Edition)
- Why is it important for construction project managers to be flexible when dealing with the many variable factors that pop up in a project?arrow_forwardWhat are some reasons for why a company would accelerate a construction project?arrow_forwardFor the design of a shallow foundation, given the following: Soil: ' = 20° c' = 52 kN/m² Unit weight, y = 15 kN/m³ Modulus of elasticity, E, = 1400 kN/m² Poisson's ratio, μs = 0.35 Foundation: L=2m B=1m Df = 1 m Calculate the ultimate bearing capacity. Use the equation: 1 - qu = c' NcFcs Fcd Fcc +qNqFqsFqdFqc + ½√BN√Fãs F√dƑxc 2 For '=20°, Nc = 14.83, N₁ = 6.4, and N₁ = 5.39. (Enter your answer to three significant figures.) qu = kN/m²arrow_forward
- A 2.0 m wide strip foundation carries a wall load of 350 kN/m in a clayey soil where y = 15 kN/m³, c' = 5.0 kN/m² and ' = 23°. The foundation depth is 1.5 m. For ' = 23°: Nc = 18.05; N₁ = 8.66; Ny = = = 8.20. Determine the factor of safety using the equation below. qu= c' NcFcs FcdFci+qNqFqsFq 1 F + gd. 'qi 2 ·BN√· FF γί Ysyd F (Enter your answer to three significant figures.) FS =arrow_forward2P -1.8 m- -1.8 m- -B Wo P -1.8 m- Carrow_forwardPart F: Progressive activity week 7 Q.F1 Pick the rural location of a project site in Victoria, and its catchment area-not bigger than 25 sqkm, and given the below information, determine the rainfall intensity for ARI 5, 50, 100 year storm event. Show all the details of the procedure. Each student must propose different length of streams and elevations. Use fig below as a sample only. Pt. E-nt 950 200 P: D-40, PC-92.0 300m 300m 000m PL.-02.0 500m HI-MAGO PLA-M 91.00 To be deemed satisfactory the solution must include: Q.F1.1.Choice of catchment location Q.F1.2. A sketch displaying length of stream and elevation Q.F1.3. Catchment's IFD obtained from the Buro of Metheorology for specified ARI Q.F1.4.Calculation of the time of concentration-this must include a detailed determination of the equivalent slope. Q.F1.5.Use must be made of the Bransby-Williams method for the determination of the equivalent slope. Q.F1.6.The graphical display of the estimation of intensities for ARI 5,50, 100…arrow_forward
- I need help finding: -The axial deflection pipe in inches. -The lateral deflection of the beam in inches -The total deflection of the beam like structure in inches ?arrow_forwardA 2.0 m wide strip foundation carries a wall load of 350 kN/m in a clayey soil where y = 17 kN/m³, c' = 5.0 kN/m² and 23°. The foundation depth is 1.5 m. For o' = 23°: Nc = 18.05; N = 8.66; N = 8.20. Determine the factor of safety using the equation below. 1 qu = c' NcFcs Fed Fci +qNqFqs FqdFqi + ½ BN F√s 1 2 (Enter your answer to three significant figures.) s Fyd Fi FS =arrow_forward1.2 m BX B 70 kN.m y = 16 kN/m³ c' = 0 6'-30° Water table Ysat 19 kN/m³ c' 0 &' = 30° A square foundation is shown in the figure above. Use FS = 6, and determine the size of the foundation. Use the Prakash and Saran theory (see equation and figures below). Suppose that F = 450 kN. Qu = BL BL[c′Nc(e)Fcs(e) + qNg(e)Fcs(e) + · 1 YBN(e) F 2 7(e) Fra(e)] (Enter your answer to two significant figures.) B: m Na(e) 60 40- 20- e/B=0 0.1 0.2 0.3 .0.4 0 0 10 20 30 40 Friction angle, ' (deg) Figure 1 Variation of Na(e) with o' Ny(e) 60 40 20 e/B=0 0.3 0.1 0.2 0.4 0 0 10 20 30 40 Friction angle, ' (deg) Figure 2 Variation of Nye) with o'arrow_forward
- K/S 46. (O المهمات الجديدة 0 المنتهية 12 المغـ ۱۱:۰۹ search ليس لديك اي مهمات ☐ ○ ☑arrow_forwardI need help setti if this problem up and solving. I keep doing something wrong.arrow_forward1.0 m (Eccentricity in one direction only)=0.15 m Call 1.5 m x 1.5m Centerline An eccentrically loaded foundation is shown in the figure above. Use FS of 4 and determine the maximum allowable load that the foundation can carry if y = 18 kN/m³ and ' = 35°. Use Meyerhof's effective area method. For '=35°, N = 33.30 and Ny = 48.03. (Enter your answer to three significant figures.) Qall = kNarrow_forward
 Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
