
The structure stiffness matrix for the truss.
Answer to Problem 14.1P
The structure stiffness matrix for the truss is shown below.
Explanation of Solution
Concept Used:
Write the expression for direction cosine in x-direction.
Here, coordinate of
Write the expression for direction cosine in x-direction.
Here, coordinate of
Write the stiffness matrix for the member.
Here, cross-sectional area of the member is
Write the expression for total structural stiffness matrix.
Here, the structural stiffness matrix is
Calculation:
The free body diagram of the truss is shown below.
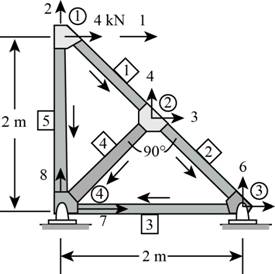
Figure (1)
Consider the member-1.
Calculate the length of member
Calculate direction cosine in x-direction.
Substitute
Calculate direction cosine in y-direction.
Substitute
The stiffness matrix for member-1 is shown below.
Substitute
Consider the member-
Calculate the length of member
Calculate direction cosine in x-direction.
Substitute
Calculate direction cosine in y-direction.
Substitute
The stiffness matrix for member-2 is shown below.
Substitute
Consider the member-
Calculate direction cosine in x-direction.
Substitute
Calculate direction cosine in y-direction.
Substitute
The stiffness matrix for member-3 is shown below.
Substitute
Consider the member-
Calculate the length of member
Calculate direction cosine in x-direction.
Substitute
Calculate direction cosine in y-direction.
Substitute
The stiffness matrix for member-4 is shown below.
Substitute
Consider the member-
Calculate direction cosine in x-direction.
Substitute
Calculate direction cosine in y-direction.
Substitute
The stiffness matrix for member-5 is shown below.
Substitute
Calculate total structural stiffness matrix.
Substitute the values of
Conclusion:
The structure stiffness matrix for the truss is shown below.
Want to see more full solutions like this?
Chapter 14 Solutions
Structural Analysis (10th Edition)
- Convert the Followingarrow_forwardSolve for the following right triangle for missing parts: - Angle A - Angle B - Side a - Areaarrow_forwardYOUR TOP STADIA CROSSHAIR IN YOUR LEVEL YEILDS A Roo READING of 7.32 FT. YOUR BOTTOM STADIA CROSSHAIR READS 6.23 FT. How FAR AWAY FROM YOUR INSTRUMENT (LEVEL) IS YOUR STATION WHERE YOUR PHilly Roo IS LOCATED:arrow_forward
- SITUATION. A uniform live load of 16 kN/m and a single concentrated live force of 34 kN are placed on the top beams. If the beams also support a uniform dead load of 3 kN/m, determinearrow_forwardComplete the profile leveling notes in Table 1. Show the arithmetic check and sample calculations of your work. Draw a neat sideview sketch showing the location of all stations and indicate on the sketch all of the numbers in your completed table.arrow_forward3. A level loop was run starting at BM 20 and going clockwise around the loop shown below in Figure 2. The given known elevation of BM 20 is 1418.013 ft. When closing the level loop, BM 20 was found to have an elevation of 1417.890 ft. (a) Adjust the elevation of each station to correct for error. Show sample calculations of your work. (b) What is the accuracy ratio of the survey? BM 20 Elev. 1418.013 2.3 mi BM 20A Observed Elev. 1234.567 2.7 mi 1.6 mil 0.9 mi BM 20B Observed Elev. 1357.913 BM 20C Observed Elev. 1396.963arrow_forward
- A W14 x 82 with 20 ft length column is part of a braced frame. The load and moments computed from service loads, and bending is about the x axis are (axial compressive dead load of 63 k; axial compressive live load of 76 k; upper dead moment of 32 ft-k; upper live moment of 56 ft-k; lower dead moment of 65 ft-k; lower live moment of 95 ft-k; the moments cause the member to bend in double curvature). Determine the lateral-torsional buckling modification factor C₁. ial live load ofarrow_forwardPROBLEM 1 Find the reaction at A and F. Compute for the force in members AB, BD, and DF. Use Method of Joints OR Method of Sections OR both. 3m B D C E 3m 100KN 3m 4marrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





