Bundle: Elementary Technical Mathematics, Loose-leaf Version, 12th + WebAssign Printed Access Card, Single-Term
12th Edition
ISBN: 9781337890199
Author: Dale Ewen
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 13.5, Problem 26E
To determine
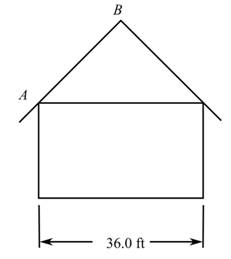
To calculate: The length AB along the roofline of the building for the provided figure.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1 Find a vector parallel to the line defined by the parametric equations
(x(t)
=
-2t
y(t)
== 1- 9t
z(t)
=
-1-t
Additionally, find a point on the line.
Find the (perpendicular) distance from the line given by the parametric equations
(x(t)
=
5+9t
y(t)
=
7t
=
2-9t
z(t)
to the point (-1, 1, −3).
Let ä(t) = (3,-2,-5)t + (7,−1, 2) and (u) = (5,0, 3)u + (−3,−9,3).
Find the acute angle (in degrees) between the lines:
Chapter 13 Solutions
Bundle: Elementary Technical Mathematics, Loose-leaf Version, 12th + WebAssign Printed Access Card, Single-Term
Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 5ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 7ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...Ch. 13.1 - Prob. 9ECh. 13.1 - Refer to right triangle ABC in Illustration 1 for...
Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 13ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 15ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 17ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 20ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Prob. 23ECh. 13.1 - Use right triangle ABC in Illustration 1 and the...Ch. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 27ECh. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 29ECh. 13.1 - Use the triangle in Illustration 2 for Exercises...Ch. 13.1 - Prob. 31ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 33ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 37ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 41ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 43ECh. 13.1 - Prob. 44ECh. 13.1 - Find the value of each trigonometric ratio rounded...Ch. 13.1 - Prob. 46ECh. 13.1 - Prob. 47ECh. 13.1 - Prob. 48ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 51ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 53ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 55ECh. 13.1 - Find each angle rounded to the nearest tenth of a...Ch. 13.1 - Prob. 57ECh. 13.1 - Prob. 58ECh. 13.1 - Prob. 59ECh. 13.1 - Prob. 60ECh. 13.1 - Prob. 61ECh. 13.1 - Prob. 62ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 64ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 66ECh. 13.1 - Find each angle rounded to the nearest hundredth...Ch. 13.1 - Prob. 68ECh. 13.1 - Prob. 69ECh. 13.1 - Prob. 70ECh. 13.1 - Prob. 71ECh. 13.1 - Prob. 72ECh. 13.1 - Prob. 73ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 5ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 7ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 9ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 17ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 19ECh. 13.2 - Using Illustration 1, find the measure of each...Ch. 13.2 - Prob. 21ECh. 13.2 - Prob. 22ECh. 13.2 - Prob. 23ECh. 13.2 - Prob. 24ECh. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Find the unknown sides of each right triangle (see...Ch. 13.3 - Prob. 11ECh. 13.3 - Prob. 12ECh. 13.3 - Prob. 13ECh. 13.3 - Prob. 14ECh. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Prob. 17ECh. 13.3 - Prob. 18ECh. 13.3 - Prob. 19ECh. 13.3 - Prob. 20ECh. 13.3 - Prob. 21ECh. 13.3 - Prob. 22ECh. 13.3 - Prob. 23ECh. 13.3 - Prob. 24ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 3ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 9ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 11ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 13ECh. 13.4 - Prob. 14ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 16ECh. 13.4 - Prob. 17ECh. 13.4 - Prob. 18ECh. 13.4 - Prob. 19ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.4 - Prob. 21ECh. 13.4 - Prob. 22ECh. 13.4 - Prob. 23ECh. 13.4 - Using Illustration 1, solve each right triangle:...Ch. 13.5 - Maria is to weld a support for a 23-m conveyor so...Ch. 13.5 - A conveyor is used to lift paper to a shredder....Ch. 13.5 - A bullet is found embedded in the wall of a room...Ch. 13.5 - The recommended safety angle of a ladder against a...Ch. 13.5 - A piece of conduit 38.0 ft long is placed across...Ch. 13.5 - Find the width of the river in Illustration 4....Ch. 13.5 - Prob. 7ECh. 13.5 - A smokestack is 180 ft high. A guy wire must be...Ch. 13.5 - A railroad track has an angle of elevation of 1.0....Ch. 13.5 - Prob. 10ECh. 13.5 - Enrico has to draft a triangular roof to a house....Ch. 13.5 - A small plane takes off from an airport and begins...Ch. 13.5 - A gauge is used to check the diameter of a crank-...Ch. 13.5 - Round metal duct runs alongside some stairs from...Ch. 13.5 - The cables attached to a TV relay tower are 110 m...Ch. 13.5 - Prob. 16ECh. 13.5 - Prob. 17ECh. 13.5 - A right circular conical tank with its point down...Ch. 13.5 - Use the right triangle in Illustration 13: a. Find...Ch. 13.5 - Prob. 20ECh. 13.5 - Twelve equally spaced holes must be drilled on a...Ch. 13.5 - Dimension x in the dovetail shown in Illustration...Ch. 13.5 - Find angle of the taper in Illustration 17....Ch. 13.5 - You need to use a metal screw with a head angle of...Ch. 13.5 - Prob. 25ECh. 13.5 - Prob. 26ECh. 13.5 - Find length x and angle A in Illustration 21....Ch. 13.5 - From the base of a building, measure out a...Ch. 13.5 - A mechanical draftsperson needs to find the...Ch. 13.5 - Prob. 30ECh. 13.5 - Prob. 31ECh. 13.5 - Prob. 32ECh. 13.5 - Solar heating and electric panels should face the...Ch. 13.5 - A lean-to is a simple shelter with three walls, a...Ch. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - Prob. 3RCh. 13 - For Exercises 1-7, see Illustration 1....Ch. 13 - Prob. 5RCh. 13 - Prob. 6RCh. 13 - Prob. 7RCh. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find angle A in Illustration 2. ILLUSTRATION 2Ch. 13 - Find angle B in Illustration 2. ILLUSTRATION 2Ch. 13 - Find side b in Illustration3. ILLUSTRATION 3Ch. 13 - Prob. 17RCh. 13 - Prob. 18RCh. 13 - Solve each right triangle:Ch. 13 - Prob. 20RCh. 13 - A satellite is directly overhead one observer...Ch. 13 - A ranger at the top of a fire tower observes the...Ch. 13 - Find the angle of slope of the symmetrical roof in...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find the value of each trigonometric ratio rounded...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find each angle rounded to the nearest tenth of a...Ch. 13 - Find angle B Illustration 1. ILLUSTRATION 1Ch. 13 - Find side a Illustration 1. ILLUSTRATION 1Ch. 13 - Find side c Illustration 1. ILLUSTRATION 1Ch. 13 - Find angle A Illustration 2. ILLUSTRATION 2Ch. 13 - Find angle B Illustration 2. ILLUSTRATION 2Ch. 13 - Find side b Illustration 2. ILLUSTRATION 2Ch. 13 - A tower 50.0 ft high has a guy wire that is...Ch. 13 - Find length x in the retaining wall in...Ch. 13 - Find angle A in the retaining wall in Illustration...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forwardA tank initially contains 50 gal of pure water. Brine containing 3 lb of salt per gallon enters the tank at 2 gal/min, and the (perfectly mixed) solution leaves the tank at 3 gal/min. Thus, the tank is empty after exactly 50 min. (a) Find the amount of salt in the tank after t minutes. (b) What is the maximum amount of salt ever in the tank?arrow_forwardDraw a picture of a normal distribution with mean 70 and standard deviation 5.arrow_forward
- What do you guess are the standard deviations of the two distributions in the previous example problem?arrow_forward1 What is the area of triangle ABC? 12 60° 60° A D B A 6√√3 square units B 18√3 square units 36√3 square units D 72√3 square unitsarrow_forwardEach answer must be justified and all your work should appear. You will be marked on the quality of your explanations. You can discuss the problems with classmates, but you should write your solutions sepa- rately (meaning that you cannot copy the same solution from a joint blackboard, for exam- ple). Your work should be submitted on Moodle, before February 7 at 5 pm. 1. True or false: (a) if E is a subspace of V, then dim(E) + dim(E) = dim(V) (b) Let {i, n} be a basis of the vector space V, where v₁,..., Un are all eigen- vectors for both the matrix A and the matrix B. Then, any eigenvector of A is an eigenvector of B. Justify. 2. Apply Gram-Schmidt orthogonalization to the system of vectors {(1,2,-2), (1, −1, 4), (2, 1, 1)}. 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show…arrow_forward
- pleasd dont use chat gptarrow_forward1. True or false: (a) if E is a subspace of V, then dim(E) + dim(E+) = dim(V) (b) Let {i, n} be a basis of the vector space V, where vi,..., are all eigen- vectors for both the matrix A and the matrix B. Then, any eigenvector of A is an eigenvector of B. Justify. 2. Apply Gram-Schmidt orthogonalization to the system of vectors {(1, 2, -2), (1, −1, 4), (2, 1, 1)}. 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show that P - Q is its own inverse. 4. Show that the Frobenius product on n x n-matrices, (A, B) = = Tr(B*A), is an inner product, where B* denotes the Hermitian adjoint of B. 5. Show that if A and B are two n x n-matrices for which {1,..., n} is a basis of eigen- vectors (for both A and B), then AB = BA. Remark: It is also true that if AB = BA, then there exists a common…arrow_forwardQuestion 1. Let f: XY and g: Y Z be two functions. Prove that (1) if go f is injective, then f is injective; (2) if go f is surjective, then g is surjective. Question 2. Prove or disprove: (1) The set X = {k € Z} is countable. (2) The set X = {k EZ,nЄN} is countable. (3) The set X = R\Q = {x ER2 countable. Q} (the set of all irrational numbers) is (4) The set X = {p.√2pQ} is countable. (5) The interval X = [0,1] is countable. Question 3. Let X = {f|f: N→ N}, the set of all functions from N to N. Prove that X is uncountable. Extra practice (not to be submitted). Question. Prove the following by induction. (1) For any nЄN, 1+3+5++2n-1 n². (2) For any nЄ N, 1+2+3++ n = n(n+1). Question. Write explicitly a function f: Nx N N which is bijective.arrow_forward
- 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show that P - Q is its own inverse.arrow_forwardAre natural logarithms used in real life ? How ? Can u give me two or three ways we can use them. Thanksarrow_forwardBy using the numbers -5;-3,-0,1;6 and 8 once, find 30arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Trigonometric Ratios; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9-eHMMpQC2k;License: Standard YouTube License, CC-BY