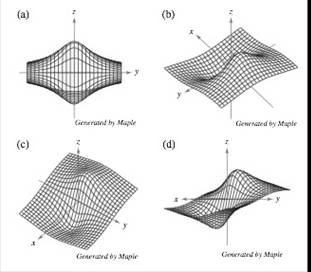
Problem 1E Problem 2E: Determine whether graph is a function. Use the graph to determine whether z is a function of x and... Problem 3E: Determining Whether an Equation Is a Function In Exercises 5-8. determine whether z is a function of... Problem 4E: Determining Whether an Equation Is a Function In Exercises 5-8. determine whether z is a function of... Problem 5E: Determining Whether an Equation Is a Function In Exercises 5-8, determine whether z is a function of... Problem 6E: Determining Whether an Equation Is a Function In Exercises 5-8, determine whether z is a function of... Problem 7E Problem 8E: Evaluating a Function In Exercises 9-20, evaluate the function at the given values of the... Problem 9E Problem 10E Problem 11E Problem 12E Problem 13E Problem 14E Problem 15E: Evaluating a Function In Exercises 9-20, evaluate the function at the given values of the... Problem 16E: Evaluating a Function In Exercises 9-20, evaluate the function at the given values of the... Problem 17E: Evaluating a Function In Exercises 9-20, evaluate the function at the given values of the... Problem 18E: Evaluating a Function In Exercises 9-20, evaluate the function at the given values of the... Problem 19E: Finding the Domain and Range of a Function In Exercises 1930, find the domain and range of the... Problem 20E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 21E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 22E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 23E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 24E Problem 25E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 26E Problem 27E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 28E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 29E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 30E: Finding the Domain and Range of a Function In Exercises 21-32, find the domain and range of the... Problem 31E: Think About It The graphs labeled (a), (b). (c). and (d) are graphs of the function... Problem 32E Problem 33E Problem 34E Problem 35E: Sketching a Surface In Exercises 35-42, describe and sketch the surface given by the function.... Problem 36E Problem 37E Problem 38E Problem 39E Problem 40E: Sketching a Surface In Exercises 35-42, describe and sketch the surface given by the function.... Problem 41E: Graphing a Function Using Technology In Exercises 43-46, use a computer algebra system to graph the... Problem 42E: Graphing a Function Using Technology In Exercises 43-46, use a computer algebra system to graph the... Problem 43E: Graphing a Function Using Technology In Exercises 43-46, use a computer algebra system to graph the... Problem 44E: Graphing a Function Using Technology In Exercises 43-46, use a computer algebra system to graph the... Problem 45E: Matching In Exercises 47-50, match the graph of the surface with one of the contour maps. [The... Problem 46E: Matching In Exercises 47-50, match the graph of the surface with one of the contour maps. [The... Problem 47E: Matching In Exercises 47-50, match the graph of the surface with one of the contour maps. [The... Problem 48E: Matching In Exercises 47-50, match the graph of the surface with one of the contour maps. [The... Problem 49E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 50E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 51E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 52E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 53E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 54E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 55E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 56E: Sketching a Contour Map In Exercises 51-58, describe the level curves of the function. Sketch a... Problem 57E: Graphing Level Curves Using Technology In Exercises 59- 62. use a graphing utility to graph six... Problem 58E: Graphing Level Curves Using Technology In Exercises 59- 62. use a graphing utility to graph six... Problem 59E: Graphing Level Curves Using Technology In Exercises 59-62. use a graphing utility to graph six level... Problem 60E: Graphing Level Curves Using Technology In Exercises 59-62. use a graphing utility to graph six level... Problem 61E Problem 62E Problem 63E Problem 64E: Conjecture Consider the function f(x,y)=xy, for x0andy0. (a) Sketch die graph of the surface given... Problem 65E: Writing In Exercises 67 and 68, use the graphs of the level curves ( c-values evenly spaced) of the... Problem 66E: Writing In Exercises 67 and 68, use the graphs of the level curves ( c - values evenly spaced) of... Problem 67E: Investment In 2016, an investment of S1000 was made in a bond earning 6% compounded annually. Assume... Problem 68E: Investment A principal of $5000 is deposited in a savings account that earns interest at a rate of r... Problem 69E: Sketching a Level Surface In Exercises 71-76. describe and sketch the graph of the level surface... Problem 70E: Sketching a Level Surface In Exercises 71-76. describe and sketch the graph of the level surface... Problem 71E: Sketching a Level Surface In Exercises 71-76. describe and sketch the graph of the level surface... Problem 72E: Sketching a Level Surface In Exercises 71-76. describe and sketch the graph of the level surface... Problem 73E: Sketching a Level Surface In Exercises 71-76. describe and sketch the graph of the level surface... Problem 74E: Sketching a Level Surface In Exercises 71-76. describe and sketch the graph of the level surface... Problem 75E: Forestry The Doyle Lux Rule is one of several methods used to determine the lumber yield of a log... Problem 76E: Queuing Model The average length of time that a customer waits in line for service is W(x,y)=1xy,xy... Problem 77E: Temperature Distribution The temperature T (in degrees Celsius) at any point (x, y) on a circular... Problem 78E: Electric Potential The electric potential V at any point (x,y) is V(x,y)=525+x2+y2. Sketch the... Problem 79E Problem 80E: Cobb-Douglas Production Function Show that the Cobb-Douglas production function z=Cxay1a can be... Problem 81E: Ideal Gas Law According to the Ideal Gas Law, PV= kT, where P is pressure, V is volume, T is... Problem 82E Problem 83E Problem 84E: Acid Rain The acidity of rainwater is measured in units called pH. A pH of 7 is neutral, smaller... Problem 85E Problem 86E: HOW DO YOU SEE IT? The contour map of the Southern Hemisphere shown in the figure was computer... Problem 87E Problem 88E Problem 89E Problem 90E Problem 91E format_list_bulleted