
Concept explainers
(a)
To find: The Inter
(a)
Answer to Problem 67E
Solution: The Inter
Explanation of Solution
Calculation: The Inter Quartile Range
Step 1: Enter the provided data in a Minitab worksheet.
Step 2: Go to Stat and select basic statistics.
Step 3: Then select Display
Step 4: Next click on Statistics tab and tick mark the option against interquartile range and click on OK twice to get the results.
From the Minitab output the Inter Quartile Range
Interpretation: The Inter Quartile Range
(b)
To find: The outliers using
(b)
Answer to Problem 67E
Solution: The value of outliers in the provided data is 428 of London. Any value above 236.5 or below –35.5 would be considered outliers as they are upper whisker and lower whisker, respectively.
Explanation of Solution
Calculation: To obtain the value of first and third quartile, follow the steps given below in Minitab,
Step 1: Enter the data in a Minitab worksheet.
Step 2: Go to Stat and select basic statistics.
Step 3: Then select Display Descriptive Statistics. Enter the name of the column containing the provided data in the variables textbox.
Step 4: Then click on Statistics tab and tick mark the option against first quartile and third quartile and click on OK twice.
The value of
The formula for upper whisker is,
where
The formula for lower whisker is,
where
Upper whisker of boxplot is found to be 236.5, so any values above 236.5 would be considered outliers and from data provided, value of 428 of London is outlier. There is no value below lower whisker.
Interpretation: Outliers refers to those data points that lie either above upper whisker and below lower whisker in boxplot. There was one outlier found in this data, and it is 428 of London.
(c)
To graph: A boxplot of the provided data and describe the distribution using it.
(c)
Explanation of Solution
Graph: Plot the boxplot in Minitab by performing the following steps,
Step 1: Enter the data into a Minitab worksheet.
Step 2: Go to ‘Graph’ and click on ‘Boxplot’.
Step 3: In the dialogue box that appears select ‘Simple’ and click OK.
Step 4: Next enter the name of the column containing the data in the filed marked as ‘Graph variables’ and click on OK.
The boxplot is obtained as shown below,
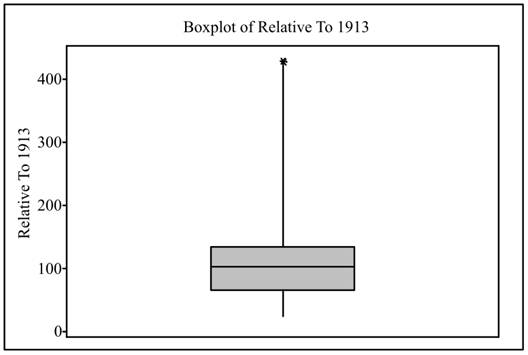
Interpretation: The boxplot is generally preferred to describe dataset having unsymmetrical distribution. The boxplot shows First quartile,
(d)
To graph: A modified boxplot and describes the distribution using it.
(d)
Explanation of Solution
Graph: Plot the modified boxplot in Minitab by performing the following steps,
Step 1: Enter the data into a Minitab worksheet.
Step 2: Go to ‘Graph’ and click on ‘Boxplot’.
Step 3: In the dialogue box that appears select ‘Simple’ and click OK.
Step 4: Next enter the name of the column containing the data in the filed marked as ‘Graph variables’ and click on OK.
The boxplot is obtained as shown below,
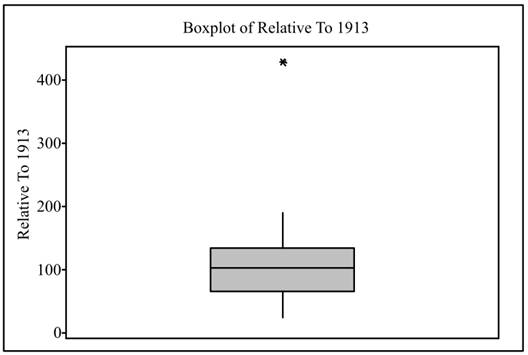
Interpretation: The modified boxplot is used to display data graphically when the distribution of data is unsymmetrical and skewed as it can clearly show outliers. In the modified boxplot it was found there is one data value which is upper outlier. This outlier is London. The modified boxplot does not display the outlier as a part of the whisker but marks the outlier away.
(e)
To graph: A stemplot of the provided data.
(e)
Explanation of Solution
Graph: Follow the steps given below to obtain the stemplot:
Step 1: Enter the data of sales in a Minitab worksheet.
Step 2: Go to Graph and select stem and leaves.
Step 3: Enter the name of the column containing the data in the Graph variables textbox and click OK.
The required stemplot is attached below,
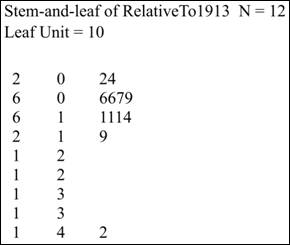
Interpretation: The stemplot of data is generally drawn when size of data is small and all the data values are positive. It shows all the data values on stemplot. In the stemplot shown above there is one outliers which is London whose data values is 428. Also the data does not seem to be symmetrically distributed.
(f)
To find: The comparison of Boxplot, Modified boxplot, and stemplot and mention advantages and disadvantages of each.
(f)
Answer to Problem 67E
Solution: In boxplot, data is displayed based on five-number summary, which included Minimum, Maximum, first quartile, third quartile, and Median and displaying the outlier as part of the whisker. In Modified boxplot also data is displayed based on five-number summary, but it displays the outliers such that they are not connected to the whiskers. In stemplot, data values are arranged in stem consisting of all digits except right most and leaves contain final digit. Advantage of boxplots is that it is suitable for unsymmetrical data while advantage of stemplot is that it shows all numerical value of data on graph itself. Disadvantage of Boxplot is that it is not suitable for unsymmetrical data while disadvantage of stemplot is that it is used only for positive numbers only and if the data size is small.
Explanation of Solution
The comparison of Boxplot, Modified boxplot, and stemplot is shown below:
Boxplot |
Modified Boxplot |
Stemplot |
|
Description |
It displays data based on |
It displays data based on five number summary including Minimum, Maximum, First quartile and Third Quartile and Median. The outliers are not displayed as part of the whiskers. |
In stemplot data values are arranged in stem consisting of all digits except right most digit and leaves contain final digit |
Advantages |
1. It displays five number summary graphically. 2. It is suitable for unsymmetrical data. |
1. It displays five number summary. 2. It is suitable for unsymmetrical data which is skewed. 3. It shows outliers clearly. |
1. It can display both symmetrical and unsymmetrical data graphically. 2. It can indicate outliers also 3. It displays all numerical values of data on stemplot. |
Disadvantages |
1. It is not suitable data set having symmetrical distribution. 2. It does not display outliers on graph. |
1. It is not suitable data set having symmetrical distribution. |
1. It is not suitable if data size is very large. 2. It is not used fornegative numbers. |
Want to see more full solutions like this?
Chapter 1 Solutions
Introduction to the Practice of Statistics
- A school counselor is conducting a research study to examine whether there is a relationship between the number of times teenagers report vaping per week and their academic performance, measured by GPA. The counselor collects data from a sample of high school students. Write the null and alternative hypotheses for this study. Clearly state your hypotheses in terms of the correlation between vaping frequency and academic performance. EditViewInsertFormatToolsTable 12pt Paragrapharrow_forwardA smallish urn contains 25 small plastic bunnies – 7 of which are pink and 18 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X = 5) ≈ (b) P(X<6) ≈ The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a) The probability that the Grinch gets exactly 6 blue marbles is [ Select ] ["≈ 0.054", "≈ 0.043", "≈ 0.061"] . (b) The probability that the Grinch gets at least 7 blue marbles is [ Select ] ["≈ 0.922", "≈ 0.905", "≈ 0.893"] . (c) The probability that the Grinch gets between 8 and 12 blue marbles (inclusive) is [ Select ] ["≈ 0.801", "≈ 0.760", "≈ 0.786"] . The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a)…arrow_forwardSuppose an experiment was conducted to compare the mileage(km) per litre obtained by competing brands of petrol I,II,III. Three new Mazda, three new Toyota and three new Nissan cars were available for experimentation. During the experiment the cars would operate under same conditions in order to eliminate the effect of external variables on the distance travelled per litre on the assigned brand of petrol. The data is given as below: Brands of Petrol Mazda Toyota Nissan I 10.6 12.0 11.0 II 9.0 15.0 12.0 III 12.0 17.4 13.0 (a) Test at the 5% level of significance whether there are signi cant differences among the brands of fuels and also among the cars. [10] (b) Compute the standard error for comparing any two fuel brands means. Hence compare, at the 5% level of significance, each of fuel brands II, and III with the standard fuel brand I. [10] �arrow_forward
- Analyze the residuals of a linear regression model and select the best response. yes, the residual plot does not show a curve no, the residual plot shows a curve yes, the residual plot shows a curve no, the residual plot does not show a curve I answered, "No, the residual plot shows a curve." (and this was incorrect). I am not sure why I keep getting these wrong when the answer seems obvious. Please help me understand what the yes and no references in the answer.arrow_forwarda. Find the value of A.b. Find pX(x) and py(y).c. Find pX|y(x|y) and py|X(y|x)d. Are x and y independent? Why or why not?arrow_forwardAnalyze the residuals of a linear regression model and select the best response.Criteria is simple evaluation of possible indications of an exponential model vs. linear model) no, the residual plot does not show a curve yes, the residual plot does not show a curve yes, the residual plot shows a curve no, the residual plot shows a curve I selected: yes, the residual plot shows a curve and it is INCORRECT. Can u help me understand why?arrow_forward
- You have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step on excel Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple…arrow_forwardHere is data with as the response variable. x y54.4 19.124.9 99.334.5 9.476.6 0.359.4 4.554.4 0.139.2 56.354 15.773.8 9-156.1 319.2Make a scatter plot of this data. Which point is an outlier? Enter as an ordered pair, e.g., (x,y). (x,y)= Find the regression equation for the data set without the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_wo= Find the regression equation for the data set with the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_w=arrow_forwardYou have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear…arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





