Chapter 13, Problem 52P

(a)

To determine

The initial upward acceleration of the balloon when it is released from sea level.

Answer to Problem 52P

  $45{\text{m/s}}^{\text{2}}$

Explanation of Solution

Given:

Radius of the balloon $\left(r\right)$ is $2.5$ m

Total mass (mass of the balloon + mass of the helium + mass of the equipment) $\left(m_{total}\right)$ is $15$ kg.

Formula used:

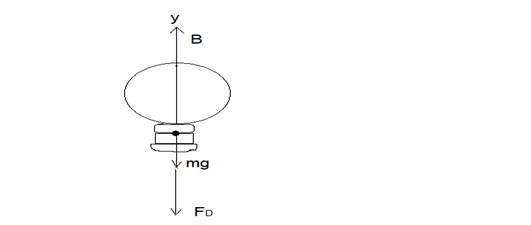
FIGURE: 1

In the figure 1, $F_D$ is the drag force

  $mg$ is weight of the balloon ( $m$ is total mass of the balloon and $g$ is acceleration due to gravity, $g=9.81$ m/s²)

  $B$ is buoyant force

Let us apply the Newton’s second law, that is $\sum F_y=m{a}_y$ to the balloon at the instant it is released

  $B-m_{balloon}g=m_{balloon}{a}_y$$\left(1\right)$

Using Archimedes principle, buoyant force $\left(B\right)$ acting on the balloon can be expressed as,

  $B=w_{displacedfluid}=m_{displacedfluid}g$

Applying $m=\rho V$ to the above equation,

  $B={\rho }_{displacedfluid}{V}_{displacedfluid}g$

  $={\rho }_{air}{V}_{balloon}g$

Since balloon is in spherical shape, volume of the balloon is,

  $V_{balloon}=\frac{4}{3}\pi r^3$

And hence, buoyant force,

  $B=\frac{4}{3}\pi r^3{\rho }_{air}g$

Where, ${\rho }_{air}$ is density of air which is equal to $1.29$ kg/m³$g$ is acceleration due to gravity, $g=9.81$ m/s²

Substituting for buoyant force in equation $\left(1\right)$ ,

  $\frac{4}{3}\pi r^3{\rho }_{air}g-m_{balloon}g=m_{balloon}{a}_y$

  $\Rightarrow a_y=\frac{1}{m_{balloon}}\left[\frac{4}{3}\pi r^3{\rho }_{air}g-m_{balloon}g\right]=\left[\frac{\frac{4}{3}\pi r^3{\rho }_{air}}{m_{balloon}}-1\right]g$$\left(2\right)$

Calculation:

Substituting the numerical values in equation $\left(2\right)$ ,

  $a_y=\left[\frac{\frac{\text{4}}{\text{3}}\text{π}{\left(\text{2}\text{.5 m}\right)}^{\text{3}}\left(\text{1}{\text{.29 kg/m}}^{\text{3}}\right)}{\text{15 kg}}\text{-1}\right]\left(\text{9}{\text{.81 m/s}}^{\text{2}}\right)=45{\text{m/s}}^{\text{2}}$

Conclusion:

The initial upward acceleration of the balloon when it is released from sea level is $45{\text{m/s}}^{\text{2}}$ .

(b)

To determine

The terminal velocity of the ascending balloon.

Answer to Problem 52P

  $7.33\text{m/s}$

Explanation of Solution

Given:

Radius of the balloon $\left(r\right)$ is $2.5$ m

Total mass (mass of the balloon + mass of the helium + mass of the equipment) $\left(m_{total}\right)$ is $15$ kg

Drag force of the balloon is $F_D=\frac{1}{2}\pi r^2\rho v^2$

Where, $r$ is radius of the balloon

  $\rho$ is density of the air

  $v$ is balloon’s ascension speed

Formula used:

Let ${\upsilon }_t$ be the terminal velocity of the balloon.

Let us apply the Newton’s second law, which is $\sum F_y=m{a}_y$ to the balloon under terminal speed condition

  $B-mg-\frac{1}{2}\pi r^2\rho {\upsilon }_t^2=0$

Substituting for $B$ from part (a),

  $\frac{4}{3}\pi r^3{\rho }_{air}g-mg-\frac{1}{2}\pi r^2\rho {\upsilon }_t^2=0$

  $\Rightarrow \frac{1}{2}\pi r^2\rho {\upsilon }_t^2=\frac{4}{3}\pi r^3{\rho }_{air}g-mg$

  $\Rightarrow {\upsilon }_t^2=\frac{1}{\frac{1}{2}\pi r^2\rho }\left[\frac{4}{3}\pi r^3{\rho }_{air}g-mg\right]=\frac{2\left[\frac{4}{3}\pi r^3{\rho }_{air}-m\right]g}{\pi r^2\rho }$

  $\Rightarrow {\upsilon }_t=\sqrt{\frac{2\left[\frac{4}{3}\pi r^3{\rho }_{air}-m\right]g}{\pi r^2\rho }}$$\left(3\right)$

Calculation:

Substituting the numerical values in equation $\left(3\right)$ ,

  ${\upsilon }_t=\sqrt{\frac{\text{2}\left[\frac{\text{4}}{\text{3}}\text{π}{\left(\text{2}\text{.5 m}\right)}^{\text{3}}\left(\text{1}{\text{.29 kg/m}}^{\text{3}}\right)\text{-15 kg}\right]\text{9}{\text{.81m/s}}^{\text{2}}}{\text{π}{\left(\text{2}\text{.5 m}\right)}^{\text{2}}\left(\text{1}{\text{.29 kg/m}}^{\text{3}}\right)}}=7.33\text{m/s}.$

Conclusion:

The terminal velocity of the ascending balloon is $7.33\text{m/s}$ .