MyLab Math with Pearson eText -- Standalone Access Card -- for Precalculus (6th Edition)
MyLab Math with Pearson eText -- Standalone Access Card -- for Precalculus (6th Edition)
6th Edition
ISBN: 9780134757834
Author: Robert F. Blitzer
Publisher: PEARSON
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.3, Problem 50PE

Use the graph of f to determine each of the following. Where applicable, use interval notation.

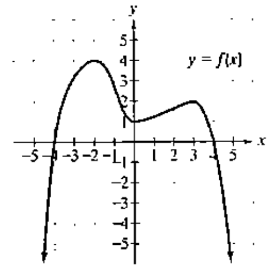
Chapter 1.3, Problem 50PE, 50. Use the graph of f to determine each of the following. Where applicable, use interval

a. the domain of f

b. the range of f

c. the x -intercepts

d. they y -intercept

e. intervals on which f is increasing

f. intervals on which f is decreasing

g. values of x for which f ( x ) ≤ 0

h. the numbers at which f has a relative maximum

i. the relative maxima of f

j. f ( − 2 )

k. the values of x for which f ( x ) − 0

i. Is f even, odd, or neither?

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.3, Problem 49PE
Next
Chapter 1.3, Problem 51PE
Students have asked these similar questions
The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.
The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.
4. Use method of separation of variable to solve the following wave equation მłu J²u subject to u(0,t) =0, for t> 0, u(л,t) = 0, for t> 0, = t> 0, at² ax²' u(x, 0) = 0, 0.01 x, ut(x, 0) = Π 0.01 (π-x), 0

Chapter 1 Solutions

MyLab Math with Pearson eText -- Standalone Access Card -- for Precalculus (6th Edition)

Ch. 1.1 - Check Point 1 Plot the points: . Ch. 1.1 - Check Point 2 Graph Select integers for x,...Ch. 1.1 - Check Point 3 Graph y=x+1. Select integers for x,...Ch. 1.1 - Check Point 4 What is the meaning of a viewing...Ch. 1.1 - Check Point 5 Identify the x- and y -intercepts.Ch. 1.1 - Check Point 6 Use the appropriate formula from...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Prob. 2CVCCh. 1.1 - Prob. 3CVCCh. 1.1 - Prob. 4CVC
Ch. 1.1 - Prob. 5CVCCh. 1.1 - Prob. 6CVCCh. 1.1 - Prob. 7CVCCh. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - In Exercises 1-12, plot the given point in a...Ch. 1.1 - In Exercises 1-12, plot the given point in a...Ch. 1.1 - Prob. 3PECh. 1.1 - In Exercises 1-12, plot the given point in a...Ch. 1.1 - Prob. 5PECh. 1.1 - Prob. 6PECh. 1.1 - Prob. 7PECh. 1.1 - Prob. 8PECh. 1.1 - In Exercises 1-12, plot the given point in a...Ch. 1.1 - In Exercises 1-12, plot the given point in a...Ch. 1.1 - Prob. 11PECh. 1.1 - Prob. 12PECh. 1.1 - Prob. 13PECh. 1.1 - Prob. 14PECh. 1.1 - Prob. 15PECh. 1.1 - Graph each equation in Exercises 13-28. Let...Ch. 1.1 - Graph each equation in Exercises 13-28. Let . 17....Ch. 1.1 - Prob. 18PECh. 1.1 - Prob. 19PECh. 1.1 - Prob. 20PECh. 1.1 - Graph each equation in Exercises 13-28. Let x =...Ch. 1.1 - Prob. 22PECh. 1.1 - Prob. 23PECh. 1.1 - Prob. 24PECh. 1.1 - Prob. 25PECh. 1.1 - Graph each equation in Exercises 13-28. Let...Ch. 1.1 - Prob. 27PECh. 1.1 - Graph each equation in Exercises 13-28. Let...Ch. 1.1 - In Exercises 29-32, match the viewing rectangle...Ch. 1.1 - Prob. 30PECh. 1.1 - Prob. 31PECh. 1.1 - Prob. 32PECh. 1.1 - Prob. 33PECh. 1.1 - Which equation corresponds to Y1 in the table? a....Ch. 1.1 - Prob. 35PECh. 1.1 - 36. Does the graph of pass through the origin? Ch. 1.1 - Prob. 37PECh. 1.1 - At which point does the graph of Y2 cross the y...Ch. 1.1 - 39. At which points do the graphs of and ...Ch. 1.1 - Prob. 40PECh. 1.1 - Prob. 41PECh. 1.1 - Prob. 42PECh. 1.1 - Prob. 43PECh. 1.1 - Prob. 44PECh. 1.1 - Prob. 45PECh. 1.1 - In Exercises 41-46, use the graph to a. determine...Ch. 1.1 - Practice Plus In Exercises 47-50, write each...Ch. 1.1 - Prob. 48PECh. 1.1 - Prob. 49PECh. 1.1 - Practice Plus In Exercises 47-50, write each...Ch. 1.1 - In Exercises 51-54, graph each equation. 51. Ch. 1.1 - In Exercises 51-54, graph each equation. 52. Ch. 1.1 - In Exercises 51-54, graph each equation. 53. Ch. 1.1 - Prob. 54PECh. 1.1 - Application Exercises The graphs show the...Ch. 1.1 - Application Exercises The graphs show the...Ch. 1.1 - Contrary to popular belief, older people do not...Ch. 1.1 - Contrary to popular belief, older people do not...Ch. 1.1 - Contrary to popular belief, older people do not...Ch. 1.1 - Prob. 60PECh. 1.1 - What is the rectangular coordinate system?Ch. 1.1 - Prob. 62PECh. 1.1 - Prob. 63PECh. 1.1 - Prob. 64PECh. 1.1 - Prob. 65PECh. 1.1 - Prob. 66PECh. 1.1 - Prob. 67PECh. 1.1 - Prob. 68PECh. 1.1 - Prob. 69PECh. 1.1 - Prob. 70PECh. 1.1 - In Exercises 71-74, determine whether each...Ch. 1.1 - Prob. 72PECh. 1.1 - Prob. 73PECh. 1.1 - In Exercises 71-74, determine whether each...Ch. 1.1 - Prob. 75PECh. 1.1 - Prob. 76PECh. 1.1 - Prob. 77PECh. 1.1 - Prob. 78PECh. 1.1 - Prob. 79PECh. 1.1 - Prob. 80PECh. 1.1 - Prob. 81PECh. 1.1 - Prob. 82PECh. 1.1 - Prob. 83PECh. 1.1 - Prob. 84PECh. 1.1 - In Exercises 83-86, select the graph that best...Ch. 1.1 - In Exercises 83-86, select the graph that best...Ch. 1.1 - Prob. 87PECh. 1.1 - Exercises 87-89 will help you prepare for the...Ch. 1.1 - Exercises 87-89 will help you prepare for the...Ch. 1.2 - Check Point 1 Find the domain and range of the...Ch. 1.2 - Check Point 2 Determine whether each relation is a...Ch. 1.2 - Check Point 3 Solve each equation for y and then...Ch. 1.2 - Check Point 4 If f(x)=x22x+7, evaluate each of the...Ch. 1.2 - Check Point 5 Graph the functions f(x)=2x and...Ch. 1.2 - Prob. 6CPCh. 1.2 - Check Point 7 Use the graph of f in Figure 1.21 on...Ch. 1.2 - Prob. 8CPCh. 1.2 - Prob. 1CVCCh. 1.2 - Prob. 2CVCCh. 1.2 - Prob. 3CVCCh. 1.2 - 4. True or false: 1 defines y as a function of x...Ch. 1.2 - Prob. 5CVCCh. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Prob. 7CVCCh. 1.2 - Prob. 8CVCCh. 1.2 - 9. The shaded set of numbers shown on the x-axis...Ch. 1.2 - Prob. 10CVCCh. 1.2 - Prob. 11CVCCh. 1.2 - Prob. 12CVCCh. 1.2 - In Exercises 1-10, determine whether each relation...Ch. 1.2 - Prob. 2PECh. 1.2 - Prob. 3PECh. 1.2 - In Exercises 1-10, determine whether each relation...Ch. 1.2 - Prob. 5PECh. 1.2 - Prob. 6PECh. 1.2 - Prob. 7PECh. 1.2 - Prob. 8PECh. 1.2 - Prob. 9PECh. 1.2 - Prob. 10PECh. 1.2 - Prob. 11PECh. 1.2 - In Exercises 11-26, determine whether each...Ch. 1.2 - Prob. 13PECh. 1.2 - In Exercises 11-26. determine whether each...Ch. 1.2 - In Exercises 11-26, determine whether each...Ch. 1.2 - In Exercises 11-26. determine whether each...Ch. 1.2 - Prob. 17PECh. 1.2 - Prob. 18PECh. 1.2 - Prob. 19PECh. 1.2 - Prob. 20PECh. 1.2 - Prob. 21PECh. 1.2 - Prob. 22PECh. 1.2 - In Exercises 11-26, determine whether each...Ch. 1.2 - Prob. 24PECh. 1.2 - In Exercises 11-26, determine whether each...Ch. 1.2 - Prob. 26PECh. 1.2 - Prob. 27PECh. 1.2 - Prob. 28PECh. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38 evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - In Exercises 27-38, evaluate each function at the...Ch. 1.2 - Prob. 39PECh. 1.2 - In Exercises 39-50, graph the given functions, f...Ch. 1.2 - Prob. 41PECh. 1.2 - In Exercises 39-50, graph the given functions, f...Ch. 1.2 - Prob. 43PECh. 1.2 - In Exercises 39-50, graph the given functions, f...Ch. 1.2 - Prob. 45PECh. 1.2 - In Exercises 39-50, graph the given functions, f...Ch. 1.2 - Prob. 47PECh. 1.2 - In Exercises 39-50, graph the given functions, f...Ch. 1.2 - Prob. 49PECh. 1.2 - In Exercises 39-50, graph the given functions, f...Ch. 1.2 - Prob. 51PECh. 1.2 - In Exercises 51-54, graph the given square root...Ch. 1.2 - Prob. 53PECh. 1.2 - Prob. 54PECh. 1.2 - In Exercises 55-64, use the vertical line test to...Ch. 1.2 - Prob. 56PECh. 1.2 - Prob. 57PECh. 1.2 - Prob. 58PECh. 1.2 - Prob. 59PECh. 1.2 - Prob. 60PECh. 1.2 - Prob. 61PECh. 1.2 - Prob. 62PECh. 1.2 - Prob. 63PECh. 1.2 - Prob. 64PECh. 1.2 - Prob. 65PECh. 1.2 - Prob. 66PECh. 1.2 - Prob. 67PECh. 1.2 - Prob. 68PECh. 1.2 - Prob. 69PECh. 1.2 - Prob. 70PECh. 1.2 - Prob. 71PECh. 1.2 - Prob. 72PECh. 1.2 - Prob. 73PECh. 1.2 - Prob. 74PECh. 1.2 - Prob. 75PECh. 1.2 - Prob. 76PECh. 1.2 - In Exercises 77-92, use the graph to determine a....Ch. 1.2 - In Exercises 77-92, use the graph to determine a....Ch. 1.2 - In Exercises 77-92, use the graph to determine a....Ch. 1.2 - Prob. 80PECh. 1.2 - Prob. 81PECh. 1.2 - Prob. 82PECh. 1.2 - Prob. 83PECh. 1.2 - Prob. 84PECh. 1.2 - Prob. 85PECh. 1.2 - Prob. 86PECh. 1.2 - Prob. 87PECh. 1.2 - Prob. 88PECh. 1.2 - Prob. 89PECh. 1.2 - Prob. 90PECh. 1.2 - Prob. 91PECh. 1.2 - Prob. 92PECh. 1.2 - In Exercises 93-94, let f(x)=x2x+4 and g(x)=3x5....Ch. 1.2 - In Exercises 93-94,let and 94. Find and . Ch. 1.2 - In Exercises 95-96, let f and g be defined by the...Ch. 1.2 - In Exercises 95-96, let f and g be defined by the...Ch. 1.2 - Prob. 97PECh. 1.2 - Prob. 98PECh. 1.2 - The Corruption Perceptions Index uses perceptions...Ch. 1.2 - Prob. 100PECh. 1.2 - Prob. 101PECh. 1.2 - Prob. 102PECh. 1.2 - Prob. 103PECh. 1.2 - Prob. 104PECh. 1.2 - Prob. 105PECh. 1.2 - Prob. 106PECh. 1.2 - Prob. 107PECh. 1.2 - Prob. 108PECh. 1.2 - Prob. 109PECh. 1.2 - Prob. 110PECh. 1.2 - Prob. 111PECh. 1.2 - Prob. 112PECh. 1.2 - Prob. 113PECh. 1.2 - Prob. 114PECh. 1.2 - Prob. 115PECh. 1.2 - Prob. 116PECh. 1.2 - Prob. 117PECh. 1.2 - Prob. 118PECh. 1.2 - Prob. 119PECh. 1.2 - Prob. 120PECh. 1.2 - Prob. 121PECh. 1.2 - Prob. 122PECh. 1.2 - Prob. 123PECh. 1.2 - Prob. 124PECh. 1.2 - Prob. 125PECh. 1.2 - Prob. 126PECh. 1.2 - Prob. 127PECh. 1.2 - Prob. 128PECh. 1.2 - Prob. 129PECh. 1.2 - Prob. 130PECh. 1.2 - ACHIEVING SUCCESS According to the Ebbinghaus...Ch. 1.2 - Prob. 132PECh. 1.2 - Prob. 133PECh. 1.2 - Exercises 132-134 will help you prepare for the...Ch. 1.3 - Check Point 1 State the intervals on which the...Ch. 1.3 - Prob. 2CPCh. 1.3 - Prob. 3CPCh. 1.3 - Prob. 4CPCh. 1.3 - Prob. 5CPCh. 1.3 - Prob. 6CPCh. 1.3 - Prob. 7CPCh. 1.3 - Prob. 8CPCh. 1.3 - Assume that f is a function defined on an open...Ch. 1.3 - Prob. 2CVCCh. 1.3 - Prob. 3CVCCh. 1.3 - Prob. 4CVCCh. 1.3 - Prob. 5CVCCh. 1.3 - Prob. 6CVCCh. 1.3 - Prob. 7CVCCh. 1.3 - Prob. 8CVCCh. 1.3 - Prob. 9CVCCh. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Prob. 11CVCCh. 1.3 - Prob. 12CVCCh. 1.3 - Practice Exercises In Exercises 1-12, use the...Ch. 1.3 - Prob. 2PECh. 1.3 - Prob. 3PECh. 1.3 - Prob. 4PECh. 1.3 - Prob. 5PECh. 1.3 - Prob. 6PECh. 1.3 - Prob. 7PECh. 1.3 - Prob. 8PECh. 1.3 - Prob. 9PECh. 1.3 - Prob. 10PECh. 1.3 - Prob. 11PECh. 1.3 - Prob. 12PECh. 1.3 - In Exercises 13-16, the graph of a function f is...Ch. 1.3 - In Exercises 13-16, the graph of a function f is...Ch. 1.3 - In Exercises 13-16, the graph of a function f is...Ch. 1.3 - In Exercises 23-16, the graph of a function f is...Ch. 1.3 - In Exercises 17-32, determine whether the graph of...Ch. 1.3 - Prob. 18PECh. 1.3 - Prob. 19PECh. 1.3 - Prob. 20PECh. 1.3 - Prob. 21PECh. 1.3 - Prob. 22PECh. 1.3 - Prob. 23PECh. 1.3 - Prob. 24PECh. 1.3 - Prob. 25PECh. 1.3 - Prob. 26PECh. 1.3 - Prob. 27PECh. 1.3 - Prob. 28PECh. 1.3 - Prob. 29PECh. 1.3 - Prob. 30PECh. 1.3 - Prob. 31PECh. 1.3 - In Exercises 17-32, determine whether the graph of...Ch. 1.3 - In Exercises 33-36, use possible symmetry to...Ch. 1.3 - In Exercises 33-36, use possible symmetry to...Ch. 1.3 - In Exercises 33-36, use possible symmetry to...Ch. 1.3 - In Exercises 33-36, use possible symmetry to...Ch. 1.3 - Prob. 37PECh. 1.3 - In Exercises 37-48, determine whether each...Ch. 1.3 - Prob. 39PECh. 1.3 - In Exercises 37-48, determine whether each...Ch. 1.3 - Prob. 41PECh. 1.3 - In Exercises 37-48, determine whether each...Ch. 1.3 - Prob. 43PECh. 1.3 - Prob. 44PECh. 1.3 - Prob. 45PECh. 1.3 - Prob. 46PECh. 1.3 - Prob. 47PECh. 1.3 - Prob. 48PECh. 1.3 - Use the graph of f to determine each of the...Ch. 1.3 - 50. Use the graph of f to determine each of the...Ch. 1.3 - Use the graph of f to determine each of the...Ch. 1.3 - Use the graph of f to determine each of the...Ch. 1.3 - In Exercise 53-58, evaluate each piecewise...Ch. 1.3 - In Exercise 53-58, evaluate each piecewise...Ch. 1.3 - In Exercise 53-58, evaluate each piecewise...Ch. 1.3 - In Exercise 53-58, evaluate each piecewise...Ch. 1.3 - In Exercise 53-58, evaluate each piecewise...Ch. 1.3 - In Exercise 53-58, evaluate each piecewise...Ch. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - Prob. 63PECh. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - Prob. 65PECh. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - Prob. 67PECh. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - In Exercises 59-70, the domain of each piecewise...Ch. 1.3 - In Exercises 71-92, find and simplify the...Ch. 1.3 - Prob. 72PECh. 1.3 - Prob. 73PECh. 1.3 - Prob. 74PECh. 1.3 - Prob. 75PECh. 1.3 - Prob. 76PECh. 1.3 - Prob. 77PECh. 1.3 - Prob. 78PECh. 1.3 - Prob. 79PECh. 1.3 - In Exercises 71-92, find and simplify the...Ch. 1.3 - Prob. 81PECh. 1.3 - In Exercises 71-92, find and simplify the...Ch. 1.3 - Prob. 83PECh. 1.3 - Prob. 84PECh. 1.3 - Prob. 85PECh. 1.3 - Prob. 86PECh. 1.3 - Prob. 87PECh. 1.3 - Prob. 88PECh. 1.3 - Prob. 89PECh. 1.3 - Prob. 90PECh. 1.3 - Prob. 91PECh. 1.3 - Prob. 92PECh. 1.3 - Prob. 93PECh. 1.3 - Prob. 94PECh. 1.3 - Prob. 95PECh. 1.3 - Prob. 96PECh. 1.3 - Prob. 97PECh. 1.3 - In Exercises 97-98, write a piecewise function...Ch. 1.3 - Prob. 99PECh. 1.3 - Prob. 100PECh. 1.3 - Prob. 101PECh. 1.3 - Prob. 102PECh. 1.3 - Prob. 103PECh. 1.3 - Prob. 104PECh. 1.3 - Prob. 105PECh. 1.3 - Prob. 106PECh. 1.3 - Prob. 107PECh. 1.3 - Prob. 108PECh. 1.3 - Prob. 109PECh. 1.3 - Here is the Federal Tax Rate Schedule X that...Ch. 1.3 - Prob. 111PECh. 1.3 - Prob. 112PECh. 1.3 - Prob. 113PECh. 1.3 - Prob. 114PECh. 1.3 - Prob. 115PECh. 1.3 - Prob. 116PECh. 1.3 - Prob. 117PECh. 1.3 - Prob. 118PECh. 1.3 - Prob. 119PECh. 1.3 - Prob. 120PECh. 1.3 - Prob. 121PECh. 1.3 - Prob. 122PECh. 1.3 - Prob. 123PECh. 1.3 - Prob. 124PECh. 1.3 - Prob. 125PECh. 1.3 - Prob. 126PECh. 1.3 - Prob. 127PECh. 1.3 - In Exercises 126-131, use a graphing utility to...Ch. 1.3 - Prob. 129PECh. 1.3 - Prob. 130PECh. 1.3 - Prob. 131PECh. 1.3 - Prob. 132PECh. 1.3 - Prob. 133PECh. 1.3 - Make Sense? In Exercises 133-136, determine...Ch. 1.3 - Prob. 135PECh. 1.3 - Prob. 136PECh. 1.3 - Prob. 137PECh. 1.3 - 138. Define a piece wise function on the intervals...Ch. 1.3 - Prob. 139PECh. 1.3 - Prob. 140PECh. 1.3 - Prob. 141PECh. 1.3 - Prob. 142PECh. 1.3 - Prob. 143PECh. 1.3 - Prob. 144PECh. 1.3 - Prob. 145PECh. 1.4 - Check Point 1 Find the slope of the line passing...Ch. 1.4 - Prob. 2CPCh. 1.4 - Check Point 3 Write an equation in point-slope...Ch. 1.4 - Check Point 4 Graph the linear function: Ch. 1.4 - Prob. 5CPCh. 1.4 - Prob. 6CPCh. 1.4 - Prob. 7CPCh. 1.4 - Prob. 8CPCh. 1.4 - Check Point 9 Use the data points (317, 57.04)...Ch. 1.4 - Prob. 1CVCCh. 1.4 - Prob. 2CVCCh. 1.4 - Prob. 3CVCCh. 1.4 - Prob. 4CVCCh. 1.4 - Prob. 5CVCCh. 1.4 - Prob. 6CVCCh. 1.4 - Prob. 7CVCCh. 1.4 - Prob. 8CVCCh. 1.4 - Prob. 9CVCCh. 1.4 - Prob. 10CVCCh. 1.4 - Prob. 11CVCCh. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Prob. 1PECh. 1.4 - Prob. 2PECh. 1.4 - Prob. 3PECh. 1.4 - In Exercises 1-10, find the slope of the line...Ch. 1.4 - Prob. 5PECh. 1.4 - Prob. 6PECh. 1.4 - Prob. 7PECh. 1.4 - Prob. 8PECh. 1.4 - Prob. 9PECh. 1.4 - Prob. 10PECh. 1.4 - Prob. 11PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 13PECh. 1.4 - Prob. 14PECh. 1.4 - Prob. 15PECh. 1.4 - Prob. 16PECh. 1.4 - Prob. 17PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 21PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 23PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 25PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 27PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 29PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 31PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 33PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 35PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - Prob. 37PECh. 1.4 - In Exercises 11-38, use the given conditions to...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - In Exercises 39-48, give the slope and y-intercept...Ch. 1.4 - Prob. 49PECh. 1.4 - Prob. 50PECh. 1.4 - Prob. 51PECh. 1.4 - In Exercises 49-58, graph each equation in a...Ch. 1.4 - Prob. 53PECh. 1.4 - Prob. 54PECh. 1.4 - Prob. 55PECh. 1.4 - In Exercises 49-58, graph each equation in a...Ch. 1.4 - Prob. 57PECh. 1.4 - Prob. 58PECh. 1.4 - Prob. 59PECh. 1.4 - In Exercises 59-66, a. Rewrite the given equation...Ch. 1.4 - Prob. 61PECh. 1.4 - In Exercises 59-66, a. Rewrite the given equation...Ch. 1.4 - Prob. 63PECh. 1.4 - In Exercises 59-66, a. Rewrite the given equation...Ch. 1.4 - Prob. 65PECh. 1.4 - In Exercises 59-66, a. Rewrite the given equation...Ch. 1.4 - Prob. 67PECh. 1.4 - In Exercises 67-72, use intercepts to graph each...Ch. 1.4 - Prob. 69PECh. 1.4 - In Exercises 67-72, use intercepts to graph each...Ch. 1.4 - Prob. 71PECh. 1.4 - In Exercises 67-72, use intercepts to graph each...Ch. 1.4 - Prob. 73PECh. 1.4 - Prob. 74PECh. 1.4 - Prob. 75PECh. 1.4 - Prob. 76PECh. 1.4 - Prob. 77PECh. 1.4 - Prob. 78PECh. 1.4 - Prob. 79PECh. 1.4 - In Exercises 79-80, find the value of y if the...Ch. 1.4 - Prob. 81PECh. 1.4 - Prob. 82PECh. 1.4 - Prob. 83PECh. 1.4 - Prob. 84PECh. 1.4 - Prob. 85PECh. 1.4 - Prob. 86PECh. 1.4 - Prob. 87PECh. 1.4 - Application Exercises Americans are getting...Ch. 1.4 - Prob. 89PECh. 1.4 - The bar graph gives the life- expectancy for...Ch. 1.4 - Prob. 91PECh. 1.4 - 92. Just as money doesn't buy happiness for...Ch. 1.4 - Prob. 93PECh. 1.4 - Describe how to write the equation of a line if...Ch. 1.4 - Prob. 95PECh. 1.4 - 96. Explain how to graph the equation . Can this...Ch. 1.4 - Prob. 97PECh. 1.4 - 98. Explain how to use intercepts to graph the...Ch. 1.4 - Prob. 99PECh. 1.4 - Prob. 100PECh. 1.4 - Prob. 101PECh. 1.4 - Prob. 102PECh. 1.4 - Prob. 103PECh. 1.4 - Prob. 104PECh. 1.4 - Make Sense? In Exercises 105-108, determine...Ch. 1.4 - Make Sense? In Exercises 105-108, determine...Ch. 1.4 - Prob. 107PECh. 1.4 - Prob. 108PECh. 1.4 - Prob. 109PECh. 1.4 - Prob. 110PECh. 1.4 - Prob. 111PECh. 1.4 - Prob. 112PECh. 1.4 - Prob. 113PECh. 1.4 - Prob. 114PECh. 1.4 - Prob. 115PECh. 1.4 - Prob. 116PECh. 1.4 - Prob. 117PECh. 1.4 - Prob. 118PECh. 1.4 - Prob. 119PECh. 1.4 - Prob. 120PECh. 1.4 - Prob. 121PECh. 1.4 - Prob. 122PECh. 1.4 - Prob. 123PECh. 1.5 - Check Point 1 Write an equation of the line...Ch. 1.5 - Prob. 2CPCh. 1.5 - Prob. 3CPCh. 1.5 - Prob. 4CPCh. 1.5 - Prob. 5CPCh. 1.5 - Prob. 6CPCh. 1.5 - Prob. 1CVCCh. 1.5 - Prob. 2CVCCh. 1.5 - Prob. 3CVCCh. 1.5 - Prob. 4CVCCh. 1.5 - Prob. 5CVCCh. 1.5 - Prob. 6CVCCh. 1.5 - Prob. 7CVCCh. 1.5 - Prob. 1PECh. 1.5 - Prob. 2PECh. 1.5 - Prob. 3PECh. 1.5 - Prob. 4PECh. 1.5 - In Exercises 5-8, use the given conditions to...Ch. 1.5 - In Exercises 5-8, use the given conditions to...Ch. 1.5 - Prob. 7PECh. 1.5 - In Exercises 5-8. use the given conditions to...Ch. 1.5 - Prob. 9PECh. 1.5 - In Exercises 9-12, use the given conditions to...Ch. 1.5 - Prob. 11PECh. 1.5 - In Exercises 9-12, use the given conditions to...Ch. 1.5 - In Exercises 13-18, find the average rate of...Ch. 1.5 - In Exercises 13-18, find the average rate of...Ch. 1.5 - Prob. 15PECh. 1.5 - In Exercises 13-I8, find the average rate of...Ch. 1.5 - Prob. 17PECh. 1.5 - In Exercises 13-18, find the average rate of...Ch. 1.5 - Prob. 19PECh. 1.5 - In Exercises 19-20, suppose that a ball is rolling...Ch. 1.5 - Prob. 21PECh. 1.5 - Prob. 22PECh. 1.5 - Prob. 23PECh. 1.5 - Prob. 24PECh. 1.5 - Prob. 25PECh. 1.5 - Prob. 26PECh. 1.5 - Prob. 27PECh. 1.5 - In Exercises 25-26, find a linear function in...Ch. 1.5 - Prob. 29PECh. 1.5 - The stated intent of the 1994 “don't ask, don't...Ch. 1.5 - The function models the number of discharges,...Ch. 1.5 - Prob. 32PECh. 1.5 - Prob. 33PECh. 1.5 - Prob. 34PECh. 1.5 - Prob. 35PECh. 1.5 - Prob. 36PECh. 1.5 - Prob. 37PECh. 1.5 - Prob. 38PECh. 1.5 - Prob. 39PECh. 1.5 - Prob. 40PECh. 1.5 - Prob. 41PECh. 1.5 - Prob. 42PECh. 1.5 - Prob. 43PECh. 1.5 - Prob. 44PECh. 1.5 - Prob. 45PECh. 1.5 - Prob. 46PECh. 1.5 - Prob. 47PECh. 1.5 - Prob. 48PECh. 1.5 - Prob. 49PECh. 1.5 - Prob. 50PECh. 1.5 - Prob. 51PECh. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - In Exercises IS, determine whether each equation...Ch. 1.5 - In Exercises 7-8, determine whether each equation...Ch. 1.5 - In Exercises 1-6, determine whether each relation...Ch. 1.5 - Use the graph of f to solve Exercises 9-24. Where...Ch. 1.5 - Use the graph of f to solve Exercises 9-24, Where...Ch. 1.5 - Use the graph of f solve Exercises 9-24, Where...Ch. 1.5 - Use the graph of f to solve Exercises 9-24 Where...Ch. 1.5 - Use the graph of f to solve Exercises 9-24. Where...Ch. 1.5 - Use the graph of f to solve Exercises 9-24. Where...Ch. 1.5 - Use the graph of f to solve Exercises 9-24. Where...Ch. 1.5 - Prob. 17MCCPCh. 1.5 - Prob. 18MCCPCh. 1.5 - Prob. 19MCCPCh. 1.5 - Prob. 20MCCPCh. 1.5 - Prob. 21MCCPCh. 1.5 - Use the graph of f to solve Exercises 9-24. Where...Ch. 1.5 - Prob. 23MCCPCh. 1.5 - Prob. 24MCCPCh. 1.5 - Prob. 25MCCPCh. 1.5 - Prob. 26MCCPCh. 1.5 - Prob. 27MCCPCh. 1.5 - Prob. 28MCCPCh. 1.5 - Prob. 29MCCPCh. 1.5 - In Exercises 27-38, graph each equation in a...Ch. 1.5 - In Exercises 27-38, graph each equation in a...Ch. 1.5 - Prob. 32MCCPCh. 1.5 - In Exercises 27-38, graph each equation in a...Ch. 1.5 - In Exercises 27-38, graph each equation in a...Ch. 1.5 - Prob. 35MCCPCh. 1.5 - Prob. 36MCCPCh. 1.5 - In Exercises 27-38, graph each equation in a...Ch. 1.5 - In Exercises 27-38, graph each equation in a...Ch. 1.5 - Prob. 39MCCPCh. 1.5 - Prob. 40MCCPCh. 1.5 - Prob. 41MCCPCh. 1.5 - Prob. 42MCCPCh. 1.5 - Prob. 43MCCPCh. 1.5 - Prob. 44MCCPCh. 1.5 - Prob. 45MCCPCh. 1.5 - Prob. 46MCCPCh. 1.5 - Prob. 47MCCPCh. 1.6 - Check Point 1 Use the graph of f(x)=|x| to obtain...Ch. 1.6 - Prob. 2CPCh. 1.6 - Prob. 3CPCh. 1.6 - Prob. 4CPCh. 1.6 - Check Point 5 Use the graph of to obtain the...Ch. 1.6 - Check Point 6 Use the graph of f(x)=x to obtain...Ch. 1.6 - Check Point 7 Use the graph of in Figure 1.65 to...Ch. 1.6 - Check Point 8 Use the graph of y=f(x) given in...Ch. 1.6 - Check Point 9 Use the graph of to graph . Ch. 1.6 - Prob. 1CVCCh. 1.6 - Prob. 2CVCCh. 1.6 - Prob. 3CVCCh. 1.6 - Prob. 4CVCCh. 1.6 - Prob. 5CVCCh. 1.6 - Prob. 6CVCCh. 1.6 - Prob. 7CVCCh. 1.6 - Prob. 1PECh. 1.6 - Prob. 2PECh. 1.6 - Prob. 3PECh. 1.6 - Prob. 4PECh. 1.6 - Prob. 5PECh. 1.6 - In Exercises 1-16, use the graph of y=f(x) to...Ch. 1.6 - Prob. 7PECh. 1.6 - In Exercises 1-16, use the graph of to graph each...Ch. 1.6 - Prob. 9PECh. 1.6 - Prob. 10PECh. 1.6 - Prob. 11PECh. 1.6 - Prob. 12PECh. 1.6 - Prob. 13PECh. 1.6 - Prob. 14PECh. 1.6 - Prob. 15PECh. 1.6 - Prob. 16PECh. 1.6 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 1.6 - Prob. 18PECh. 1.6 - Prob. 19PECh. 1.6 - In Exercises 17-32, use the graph of y=f(x) to...Ch. 1.6 - Prob. 21PECh. 1.6 - Prob. 22PECh. 1.6 - Prob. 23PECh. 1.6 - Prob. 24PECh. 1.6 - Prob. 25PECh. 1.6 - Prob. 26PECh. 1.6 - Prob. 27PECh. 1.6 - Prob. 28PECh. 1.6 - Prob. 29PECh. 1.6 - Prob. 30PECh. 1.6 - Prob. 31PECh. 1.6 - Prob. 32PECh. 1.6 - Prob. 33PECh. 1.6 - Prob. 34PECh. 1.6 - Prob. 35PECh. 1.6 - Prob. 36PECh. 1.6 - Prob. 37PECh. 1.6 - Prob. 38PECh. 1.6 - Prob. 39PECh. 1.6 - Prob. 40PECh. 1.6 - Prob. 41PECh. 1.6 - Prob. 42PECh. 1.6 - Prob. 43PECh. 1.6 - Prob. 44PECh. 1.6 - Prob. 45PECh. 1.6 - Prob. 46PECh. 1.6 - Prob. 47PECh. 1.6 - Prob. 48PECh. 1.6 - Prob. 49PECh. 1.6 - Prob. 50PECh. 1.6 - Prob. 51PECh. 1.6 - Prob. 52PECh. 1.6 - Prob. 53PECh. 1.6 - Prob. 54PECh. 1.6 - Prob. 55PECh. 1.6 - Prob. 56PECh. 1.6 - Prob. 57PECh. 1.6 - Prob. 58PECh. 1.6 - Prob. 59PECh. 1.6 - In Exercise 53-66, begin by graphing the standard...Ch. 1.6 - Prob. 61PECh. 1.6 - In Exercise 53-66, begin by graphing the standard...Ch. 1.6 - Prob. 63PECh. 1.6 - In Exercise 53-66, begin by graphing the standard...Ch. 1.6 - Prob. 65PECh. 1.6 - In Exercise 53-66, begin by graphing the standard...Ch. 1.6 - Prob. 67PECh. 1.6 - Prob. 68PECh. 1.6 - Prob. 69PECh. 1.6 - Prob. 70PECh. 1.6 - Prob. 71PECh. 1.6 - Prob. 72PECh. 1.6 - Prob. 73PECh. 1.6 - Prob. 74PECh. 1.6 - Prob. 75PECh. 1.6 - In Exercises 67-80, begin by graphing the square...Ch. 1.6 - Prob. 77PECh. 1.6 - In Exercises 67-80, begin by graphing the square...Ch. 1.6 - Prob. 79PECh. 1.6 - In Exercises 67-80, begin by graphing the square...Ch. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - Prob. 82PECh. 1.6 - Prob. 83PECh. 1.6 - Prob. 84PECh. 1.6 - Prob. 85PECh. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - Prob. 87PECh. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - Prob. 91PECh. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - Prob. 93PECh. 1.6 - In Exercises 81-94, begin by graphing the absolute...Ch. 1.6 - Prob. 95PECh. 1.6 - Prob. 96PECh. 1.6 - Prob. 97PECh. 1.6 - Prob. 98PECh. 1.6 - Prob. 99PECh. 1.6 - Prob. 100PECh. 1.6 - Prob. 101PECh. 1.6 - Prob. 102PECh. 1.6 - Prob. 103PECh. 1.6 - In Exercises 95-106, begin by graphing the...Ch. 1.6 - Prob. 105PECh. 1.6 - Prob. 106PECh. 1.6 - Prob. 107PECh. 1.6 - Prob. 108PECh. 1.6 - Prob. 109PECh. 1.6 - In Exercises 107-118, begin by graphing the cube...Ch. 1.6 - Prob. 111PECh. 1.6 - In Exercises 107-118, begin by graphing the cube...Ch. 1.6 - Prob. 113PECh. 1.6 - In Exercises 107-118, begin by graphing the cube...Ch. 1.6 - Prob. 115PECh. 1.6 - In Exercises 107-118, begin by graphing the cube...Ch. 1.6 - Prob. 117PECh. 1.6 - In Exercises 107-118, begin by graphing the cube...Ch. 1.6 - Prob. 119PECh. 1.6 - Prob. 120PECh. 1.6 - Prob. 121PECh. 1.6 - Prob. 122PECh. 1.6 - Prob. 123PECh. 1.6 - Prob. 124PECh. 1.6 - Prob. 125PECh. 1.6 - Prob. 126PECh. 1.6 - Prob. 127PECh. 1.6 - Prob. 128PECh. 1.6 - Prob. 129PECh. 1.6 - Prob. 130PECh. 1.6 - Prob. 131PECh. 1.6 - Prob. 132PECh. 1.6 - Prob. 133PECh. 1.6 - Prob. 134PECh. 1.6 - Prob. 135PECh. 1.6 - Prob. 136PECh. 1.6 - Prob. 137PECh. 1.6 - Prob. 138PECh. 1.6 - Prob. 139PECh. 1.6 - Make Sense? During the winter, you program your...Ch. 1.6 - Prob. 141PECh. 1.6 - In Exercises 141-144, determine whether each...Ch. 1.6 - Prob. 143PECh. 1.6 - In Exercises 141-144, determine whether each...Ch. 1.6 - Prob. 145PECh. 1.6 - In Exercises 145-148, functions f and g are...Ch. 1.6 - Prob. 147PECh. 1.6 - In Exercises 145-148, functions f and g are...Ch. 1.6 - Prob. 149PECh. 1.6 - Prob. 150PECh. 1.6 - Prob. 151PECh. 1.6 - Prob. 152PECh. 1.6 - Prob. 153PECh. 1.6 - Prob. 154PECh. 1.6 - Prob. 155PECh. 1.6 - Prob. 156PECh. 1.6 - Prob. 157PECh. 1.6 - Prob. 158PECh. 1.7 - Check point 1 Find the domain of each function: a....Ch. 1.7 - Check Point 2 Let and . Find each of the...Ch. 1.7 - Prob. 3CPCh. 1.7 - Check Point 4 Use the birth and death models from...Ch. 1.7 - Prob. 5CPCh. 1.7 - Prob. 6CPCh. 1.7 - Prob. 7CPCh. 1.7 - Prob. 1CVCCh. 1.7 - Prob. 2CVCCh. 1.7 - Prob. 3CVCCh. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Prob. 5CVCCh. 1.7 - Prob. 6CVCCh. 1.7 - Prob. 7CVCCh. 1.7 - Prob. 8CVCCh. 1.7 - Prob. 9CVCCh. 1.7 - Prob. 10CVCCh. 1.7 - Prob. 11CVCCh. 1.7 - Prob. 12CVCCh. 1.7 - Prob. 13CVCCh. 1.7 - Prob. 14CVCCh. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Prob. 16CVCCh. 1.7 - Prob. 1PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 3PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 5PECh. 1.7 - Prob. 6PECh. 1.7 - Prob. 7PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 10PECh. 1.7 - Prob. 11PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 14PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 16PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 21PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 23PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 25PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - Prob. 29PECh. 1.7 - In Exercises 1-30, find the domain of each...Ch. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - Prob. 33PECh. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - Prob. 35PECh. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - Prob. 37PECh. 1.7 - In Exercises 31-50, find f+g,fg,fg, and 1g ....Ch. 1.7 - Prob. 39PECh. 1.7 - In Exercises 31-50, find f+g,fg,fg, and 1g ....Ch. 1.7 - Prob. 41PECh. 1.7 - In Exercises 31-50, find f+g,fg,fg, and 1g ....Ch. 1.7 - Prob. 43PECh. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - In Exercises 31-50, find f+g,fg,fg, and 1g ....Ch. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - Prob. 47PECh. 1.7 - In Exercises 31-50, find , and . Determine the...Ch. 1.7 - Prob. 49PECh. 1.7 - In Exercises 31-50, find f+g,fg,fg, and 1g ....Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 51. Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 52. Ch. 1.7 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 54. Ch. 1.7 - Prob. 55PECh. 1.7 - In Exercises 51-66, find a. b. c. d. . 56. Ch. 1.7 - Prob. 57PECh. 1.7 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 59. Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 60. Ch. 1.7 - Prob. 61PECh. 1.7 - In Exercises 51-66, find a. (fg)(x) b. (gf)(x) c....Ch. 1.7 - Prob. 63PECh. 1.7 - In Exercises 51-66, find a. b. c. d. . 64. Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 65. Ch. 1.7 - In Exercises 51-66, find a. b. c. d. . 66. Ch. 1.7 - Prob. 67PECh. 1.7 - In Exercises 67-74, find a. b. the domain of...Ch. 1.7 - Prob. 69PECh. 1.7 - In Exercises 67-74, find a. b. the domain of...Ch. 1.7 - Prob. 71PECh. 1.7 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 1.7 - Prob. 73PECh. 1.7 - In Exercises 67-74, find a. (fg)(x) b. the domain...Ch. 1.7 - In Exercises 75-82, express the given function h...Ch. 1.7 - Prob. 76PECh. 1.7 - Prob. 77PECh. 1.7 - Prob. 78PECh. 1.7 - Prob. 79PECh. 1.7 - In Exercises 75-82, express the given function h...Ch. 1.7 - Prob. 81PECh. 1.7 - Prob. 82PECh. 1.7 - Prob. 83PECh. 1.7 - Prob. 84PECh. 1.7 - Prob. 85PECh. 1.7 - Prob. 86PECh. 1.7 - Prob. 87PECh. 1.7 - Prob. 88PECh. 1.7 - Prob. 89PECh. 1.7 - Prob. 90PECh. 1.7 - Prob. 91PECh. 1.7 - Prob. 92PECh. 1.7 - Prob. 93PECh. 1.7 - Prob. 94PECh. 1.7 - Prob. 95PECh. 1.7 - Prob. 96PECh. 1.7 - Prob. 97PECh. 1.7 - The bar graph shows the population of the United...Ch. 1.7 - Prob. 99PECh. 1.7 - A department store has two locations in a city....Ch. 1.7 - Prob. 101PECh. 1.7 - The regular price of a pair of jeans is x dollars....Ch. 1.7 - Prob. 103PECh. 1.7 - If equations for f and g are given, explain how to...Ch. 1.7 - Prob. 105PECh. 1.7 - Prob. 106PECh. 1.7 - Describe the values of x that must be excluded...Ch. 1.7 - Prob. 108PECh. 1.7 - Prob. 109PECh. 1.7 - Prob. 110PECh. 1.7 - Prob. 111PECh. 1.7 - Prob. 112PECh. 1.7 - Make Sense? In Exercise 110-113, determine whether...Ch. 1.7 - Prob. 114PECh. 1.7 - Prob. 115PECh. 1.7 - In Exercises 114-117, determine whether each...Ch. 1.7 - Prob. 117PECh. 1.7 - Prob. 118PECh. 1.7 - Prob. 119PECh. 1.7 - Prob. 120PECh. 1.7 - Prob. 121PECh. 1.7 - Prob. 122PECh. 1.7 - Prob. 123PECh. 1.7 - Exercises 123-125 will help you prepare for the...Ch. 1.7 - Exercises 123-125 will help you prepare for the...Ch. 1.8 - Check Point 1 Show that each function is the...Ch. 1.8 - Check Point 2 Find the inverse of . Ch. 1.8 - Check Point 3 Find the inverse of f(x)=4x31.Ch. 1.8 - Prob. 4CPCh. 1.8 - Check Point 5 Which of the following graphs...Ch. 1.8 - Prob. 6CPCh. 1.8 - Prob. 7CPCh. 1.8 - 1. The notation means the ____ of the function...Ch. 1.8 - Prob. 2CVCCh. 1.8 - Prob. 3CVCCh. 1.8 - Prob. 4CVCCh. 1.8 - Prob. 1PECh. 1.8 - Prob. 2PECh. 1.8 - Prob. 3PECh. 1.8 - Prob. 4PECh. 1.8 - Prob. 5PECh. 1.8 - Prob. 6PECh. 1.8 - Prob. 7PECh. 1.8 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 1.8 - Prob. 9PECh. 1.8 - In Exercises 1-10, find f(g(x)) and g(f(x)) and...Ch. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 13PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 15PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 17PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 19PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 21PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 23PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 25PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 27PECh. 1.8 - The functions in Exercises 11-28 are all...Ch. 1.8 - Prob. 29PECh. 1.8 - Which graphs in Exercises 29-34 represent...Ch. 1.8 - Prob. 31PECh. 1.8 - Prob. 32PECh. 1.8 - Prob. 33PECh. 1.8 - Prob. 34PECh. 1.8 - Prob. 35PECh. 1.8 - Prob. 36PECh. 1.8 - Prob. 37PECh. 1.8 - Prob. 38PECh. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for . b....Ch. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - In Exercises 39-52, a. Find an equation for f1(x)....Ch. 1.8 - Prob. 53PECh. 1.8 - Prob. 54PECh. 1.8 - Prob. 55PECh. 1.8 - In Exercises 53-58, f and g are defined by the...Ch. 1.8 - Prob. 57PECh. 1.8 - In Exercises 53-58, f and g are defined by the...Ch. 1.8 - In Exercises 59-64, let...Ch. 1.8 - Prob. 60PECh. 1.8 - Prob. 61PECh. 1.8 - Prob. 62PECh. 1.8 - Prob. 63PECh. 1.8 - 64. f(g[h(1)]) Ch. 1.8 - Prob. 65PECh. 1.8 - In most societies, women say they prefer to marry...Ch. 1.8 - Prob. 67PECh. 1.8 - A study of 900 working women in Texas showed that...Ch. 1.8 - Prob. 69PECh. 1.8 - Prob. 70PECh. 1.8 - Prob. 71PECh. 1.8 - Prob. 72PECh. 1.8 - Prob. 73PECh. 1.8 - Prob. 74PECh. 1.8 - Prob. 75PECh. 1.8 - Prob. 76PECh. 1.8 - Prob. 77PECh. 1.8 - Prob. 78PECh. 1.8 - Prob. 79PECh. 1.8 - Prob. 80PECh. 1.8 - Prob. 81PECh. 1.8 - Prob. 82PECh. 1.8 - Prob. 83PECh. 1.8 - Prob. 84PECh. 1.8 - Prob. 85PECh. 1.8 - Prob. 86PECh. 1.8 - Prob. 87PECh. 1.8 - Prob. 88PECh. 1.8 - Prob. 89PECh. 1.8 - Prob. 90PECh. 1.8 - Prob. 91PECh. 1.8 - Prob. 92PECh. 1.8 - Prob. 93PECh. 1.8 - Prob. 94PECh. 1.8 - Prob. 95PECh. 1.8 - Prob. 96PECh. 1.8 - Prob. 97PECh. 1.8 - Prob. 98PECh. 1.8 - Prob. 99PECh. 1.8 - Prob. 100PECh. 1.8 - Prob. 101PECh. 1.8 - Prob. 102PECh. 1.8 - Prob. 103PECh. 1.8 - Prob. 104PECh. 1.8 - Exercises 103-105 will help you prepare for the...Ch. 1.9 - Check Point 1 Find the distance between (-1, -3)...Ch. 1.9 - Prob. 2CPCh. 1.9 - Prob. 3CPCh. 1.9 - Prob. 4CPCh. 1.9 - Prob. 5CPCh. 1.9 - Prob. 6CPCh. 1.9 - Prob. 1CVCCh. 1.9 - Prob. 2CVCCh. 1.9 - Prob. 3CVCCh. 1.9 - Prob. 4CVCCh. 1.9 - Prob. 5CVCCh. 1.9 - Prob. 6CVCCh. 1.9 - Prob. 1PECh. 1.9 - Prob. 2PECh. 1.9 - Prob. 3PECh. 1.9 - Prob. 4PECh. 1.9 - Prob. 5PECh. 1.9 - Prob. 6PECh. 1.9 - Prob. 7PECh. 1.9 - Prob. 8PECh. 1.9 - Prob. 9PECh. 1.9 - In Exercises 1-18, find the distance between each...Ch. 1.9 - Prob. 11PECh. 1.9 - In Exercises 1-18, find the distance between each...Ch. 1.9 - Prob. 13PECh. 1.9 - In Exercises 1-18, find the distance between each...Ch. 1.9 - Prob. 15PECh. 1.9 - In Exercises 1-18, find the distance between each...Ch. 1.9 - Prob. 17PECh. 1.9 - In Exercises 1-18, find the distance between each...Ch. 1.9 - Prob. 19PECh. 1.9 - In Exercises 19-30, find the midpoint of each line...Ch. 1.9 - Prob. 21PECh. 1.9 - In Exercises 19-30, find die midpoint of each line...Ch. 1.9 - Prob. 23PECh. 1.9 - In Exercises 19-30, find die midpoint of each line...Ch. 1.9 - Prob. 25PECh. 1.9 - In Exercises 19-30, find the midpoint of each Hue...Ch. 1.9 - Prob. 27PECh. 1.9 - In Exercises 19-30, find the midpoint of each line...Ch. 1.9 - Prob. 29PECh. 1.9 - In Exercises 19-30, find die midpoint of each line...Ch. 1.9 - Prob. 31PECh. 1.9 - Prob. 32PECh. 1.9 - Prob. 33PECh. 1.9 - Prob. 34PECh. 1.9 - Prob. 35PECh. 1.9 - Prob. 36PECh. 1.9 - Prob. 37PECh. 1.9 - Prob. 38PECh. 1.9 - Prob. 39PECh. 1.9 - Prob. 40PECh. 1.9 - Prob. 41PECh. 1.9 - Prob. 42PECh. 1.9 - Prob. 43PECh. 1.9 - Prob. 44PECh. 1.9 - Prob. 45PECh. 1.9 - Prob. 46PECh. 1.9 - Prob. 47PECh. 1.9 - Prob. 48PECh. 1.9 - Prob. 49PECh. 1.9 - Prob. 50PECh. 1.9 - Prob. 51PECh. 1.9 - Prob. 52PECh. 1.9 - Prob. 53PECh. 1.9 - Prob. 54PECh. 1.9 - Prob. 55PECh. 1.9 - Prob. 56PECh. 1.9 - Prob. 57PECh. 1.9 - Prob. 58PECh. 1.9 - Prob. 59PECh. 1.9 - Prob. 60PECh. 1.9 - Prob. 61PECh. 1.9 - Prob. 62PECh. 1.9 - Prob. 63PECh. 1.9 - Prob. 64PECh. 1.9 - Prob. 65PECh. 1.9 - Prob. 66PECh. 1.9 - Prob. 67PECh. 1.9 - Prob. 68PECh. 1.9 - Prob. 69PECh. 1.9 - Prob. 70PECh. 1.9 - Application Exercises The cellphone screen shows...Ch. 1.9 - Application Exercises The cellphone screen shows...Ch. 1.9 - Prob. 73PECh. 1.9 - Prob. 74PECh. 1.9 - Prob. 75PECh. 1.9 - Prob. 76PECh. 1.9 - Prob. 77PECh. 1.9 - Prob. 78PECh. 1.9 - Prob. 79PECh. 1.9 - Prob. 80PECh. 1.9 - Prob. 81PECh. 1.9 - Prob. 82PECh. 1.9 - Prob. 83PECh. 1.9 - Prob. 84PECh. 1.9 - Prob. 85PECh. 1.9 - Make Sense? In Exercises 86-89, determine whether...Ch. 1.9 - Prob. 87PECh. 1.9 - Prob. 88PECh. 1.9 - Prob. 89PECh. 1.9 - Prob. 90PECh. 1.9 - Prob. 91PECh. 1.9 - Prob. 92PECh. 1.9 - Prob. 93PECh. 1.9 - Prob. 94PECh. 1.9 - Prove the midpoint formula by using the following...Ch. 1.9 - Prob. 96PECh. 1.9 - Prob. 97PECh. 1.9 - Prob. 98PECh. 1.9 - Prob. 99PECh. 1.9 - Prob. 100PECh. 1.9 - Exercises 101-103 will help you prepare for the...Ch. 1.9 - Prob. 102PECh. 1.9 - Prob. 103PECh. 1.10 - Check Point 1 You are choosing between two texting...Ch. 1.10 - Check Point 2 On a certain route, an airline...Ch. 1.10 - Check Point 3 A machine produces open boxes using...Ch. 1.10 - Check Point 4 You have 200 feet of fencing to...Ch. 1.10 - Check Point 5 A cylindrical can is to hold 1...Ch. 1.10 - Check Point 6 Let P (x, y ) be a point on the...Ch. 1.10 - Fill in each blank so that the resulting statement...Ch. 1.10 - Fill in each blank so that the resulting statement...Ch. 1.10 - Fill in each blank so that the resulting statement...Ch. 1.10 - Fill in each blank so that the resulting statement...Ch. 1.10 - Fill in each blank so that the resulting statement...Ch. 1.10 - A car rental agency charges $200 per week plus...Ch. 1.10 - A car rental agency charges $180 per week plus...Ch. 1.10 - One yardstick for measuring how steadily-if...Ch. 1.10 - According to the National Center for Health...Ch. 1.10 - The bus fare in a city is $1.25. People who use...Ch. 1.10 - A discount pass for a bridge costs $21 per month....Ch. 1.10 - You are choosing between two plans at a discount...Ch. 1.10 - You are choosing between two plans at a discount...Ch. 1.10 - A football team plays in a large stadium. With a...Ch. 1.10 - A base ball team plays in a large stadium. With a...Ch. 1.10 - On a certain route, an airline carries 9000...Ch. 1.10 - On a certain route, an airline carries 7000...Ch. 1.10 - The annual yield per lemon tree is fairly constant...Ch. 1.10 - The annual yield per orange tree is fairly...Ch. 1.10 - An open box is made from a square piece of...Ch. 1.10 - An open box is made from a square piece of...Ch. 1.10 - A rain gutter is made from sheets of aluminum that...Ch. 1.10 - A piece of wire is 8 inches long. The wire is cut...Ch. 1.10 - The sum of two numbers is 66. Express the product...Ch. 1.10 - The sum of two numbers is 50. Express the product...Ch. 1.10 - You have 800 feet of fencing to enclose a...Ch. 1.10 - You have 600 feet of fencing to enclose a...Ch. 1.10 - As in Exercise 21, you have 800 feet of fencing to...Ch. 1.10 - As in Exercise 22, you have 600 feet of fencing to...Ch. 1.10 - You have 1000 feet of fencing to enclose a...Ch. 1.10 - You have 1200 feet of fencing to enclose a...Ch. 1.10 - A new running track is to be constructed in the...Ch. 1.10 - Work Exercise 27 if the length of the track is...Ch. 1.10 - A contractor is to build a warehouse whose...Ch. 1.10 - The area of a rectangular garden is 125 square...Ch. 1.10 - The figure shows an open box with a square base....Ch. 1.10 - The figure shows an open box with a square base...Ch. 1.10 - The figure shows a package whose front is a...Ch. 1.10 - Work Exercise 33 if the length plus girth of the...Ch. 1.10 - Let P(x, y) be a point on the graph of y=x24....Ch. 1.10 - Let P(x,y) be a point on the graph of y=x28....Ch. 1.10 - Let P(x,y) be a point on the graph of y=x. Express...Ch. 1.10 - Let P (x, y) be a point on the graph of y=x....Ch. 1.10 - The figure shows a rectangle with two vertices on...Ch. 1.10 - The figure shows a rectangle with two vertices on...Ch. 1.10 - Two vertical poles of length t feet and 8 feet,...Ch. 1.10 - Towns A and B are located 6 miles and 3 miles,...Ch. 1.10 - In Exercises 43-44, express the area of each...Ch. 1.10 - In Exercises 43-44, express the area of each...Ch. 1.10 - Exercises 45-46, express the volume of each...Ch. 1.10 - Exercises 46-46, express the volume of each...Ch. 1.10 - Throughout this section, we started with familiar...Ch. 1.10 - Describe what should be displayed on the screen of...Ch. 1.10 - In Exercise 9(b) or Exercise 10(b), describe what...Ch. 1.10 - In Exercise 13(b) or 14(b), describe what...Ch. 1.10 - In Exercise 31 or 32, describe what important...Ch. 1.10 - Use a graphing utility to graph the function that...Ch. 1.10 - Use a graphing utility to graph the two functions,...Ch. 1.10 - Use a graphing utility to graph the...Ch. 1.10 - Use a graphing utility to graph the area function,...Ch. 1.10 - Use a graphing utility to graph the area function,...Ch. 1.10 - Use the maximum or minimum function feature of a...Ch. 1.10 - Make Sense? In Exercises 59-62, determine whether...Ch. 1.10 - Make Sense? In Exercises 59-62, determine whether...Ch. 1.10 - Make Sense? In Exercises 59-62, determine whether...Ch. 1.10 - Make Sense? In Exercises 59-62, determine whether...Ch. 1.10 - You are on an island 2 miles from the nearest...Ch. 1.10 - A pool measuring 20 meters by 10 meters is...Ch. 1.10 - The figure shows a Norman window that has the...Ch. 1.10 - The figure shows water running into a container in...Ch. 1.10 - In Exercises 67-69, solve each equation....Ch. 1.10 - In Exercises 67-69, solve each equation. 2x2+x=6...Ch. 1.10 - In Exercises 67-69, solve each equation. 3x+7+1=x...Ch. 1.10 - Exercises 70-72 will help you prepare for the...Ch. 1.10 - Exercises 70-72 will help you prepare for the...Ch. 1.10 - Exercises 70-72 will help you prepare for the...Ch. 1 - Graph each equation in Exercises 1-4. Let 1. Ch. 1 - Graph each equation in Exercises 1-4. Let...Ch. 1 - Graph each equation in Exercises 1-4. Let...Ch. 1 - Prob. 4RECh. 1 - 5. What does a by viewing rectangle mean? Draw...Ch. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Salary after College. In 2010; Monster College...Ch. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Salary after College. In 2010, Monster College...Ch. 1 - Prob. 15RECh. 1 - In Exercises 1-3, determine whether each relation...Ch. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - In Exercises 20-21, find each of the following: a....Ch. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - In Exercises 31-32, the domain of each piecewise...Ch. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - In Exercises 41-44, use the given conditions to...Ch. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - A person standing on the roof of a building throws...Ch. 1 - In Exercises 55-59, use the graph of to graph...Ch. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - Prob. 84RECh. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - In Exercises 73-75, begin by graphing the cube...Ch. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - In Exercises 76-81, find /he domain of each...Ch. 1 - Prob. 93RECh. 1 - Prob. 94RECh. 1 - Prob. 95RECh. 1 - Prob. 96RECh. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 100RECh. 1 - Prob. 101RECh. 1 - Prob. 102RECh. 1 - Prob. 103RECh. 1 - Prob. 104RECh. 1 - Prob. 105RECh. 1 - Prob. 106RECh. 1 - Prob. 107RECh. 1 - Prob. 108RECh. 1 - Prob. 109RECh. 1 - Prob. 110RECh. 1 - Prob. 111RECh. 1 - Prob. 112RECh. 1 - Prob. 113RECh. 1 - Prob. 114RECh. 1 - Prob. 115RECh. 1 - Prob. 116RECh. 1 - Prob. 117RECh. 1 - Prob. 118RECh. 1 - Prob. 119RECh. 1 - Prob. 120RECh. 1 - Prob. 121RECh. 1 - Prob. 122RECh. 1 - Prob. 123RECh. 1 - Prob. 124RECh. 1 - Prob. 125RECh. 1 - Prob. 126RECh. 1 - Prob. 127RECh. 1 - 128. You are choosing between two texting plans....Ch. 1 - A 400-room hotel can rent every one of its rooms...Ch. 1 - Prob. 130RECh. 1 - Prob. 131RECh. 1 - Prob. 132RECh. 1 - List by letter all relation that are not function...Ch. 1 - Prob. 2TCh. 1 - Prob. 3TCh. 1 - Prob. 4TCh. 1 - Prob. 5TCh. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Prob. 8TCh. 1 - Prob. 9TCh. 1 - Prob. 10TCh. 1 - Prob. 11TCh. 1 - Prob. 12TCh. 1 - Prob. 13TCh. 1 - Prob. 14TCh. 1 - Prob. 15TCh. 1 - Prob. 16TCh. 1 - Prob. 17TCh. 1 - Prob. 18TCh. 1 - Prob. 19TCh. 1 - Prob. 20TCh. 1 - Prob. 21TCh. 1 - Prob. 22TCh. 1 - Prob. 23TCh. 1 - Prob. 24TCh. 1 - Prob. 25TCh. 1 - Prob. 26TCh. 1 - Prob. 27TCh. 1 - Prob. 28TCh. 1 - Prob. 29TCh. 1 - Prob. 30TCh. 1 - Prob. 31TCh. 1 - Prob. 32TCh. 1 - Prob. 33TCh. 1 - Prob. 34TCh. 1 - Prob. 35TCh. 1 - In 1980, the winning time for women in the Olympic...Ch. 1 - The annual yield per walnut tree is fairly...Ch. 1 - Prob. 38TCh. 1 - Prob. 39T
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY