College Algebra, Books a la Carte Edition Plus NEW MyMathLab -- Access Card Package (6th Edition)
6th Edition
ISBN: 9780321869357
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 1.3, Problem 24PE
Even as Americans increasingly view a college education as essential for success, many believe that a college education is becoming less available to qualified students. Exercises 23–24 are based on the data displayed by the graphs.
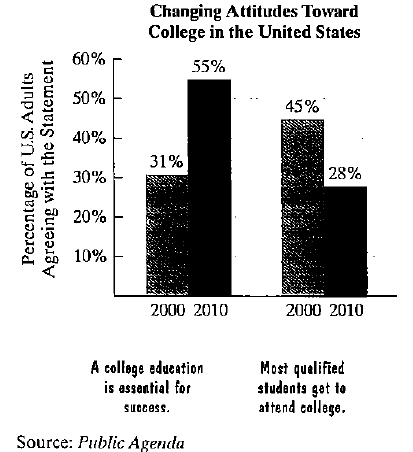
The data displayed by the graph at the bottom of the previous page indicate that in 2000, 45% of U.S. adults believed most qualified students get to attend college. For the period from 2000 through 2010, the percentage who believed that a college education is available to most qualified students decreased by approximately 1.7 each year. If this trend continues, by which year will only 11% of all American adults believe that most qualified students get to attend college?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
How long is a guy wire reaching from the top of a
15-foot pole to a point on the ground
9-feet from the pole?
Question content area bottom
Part 1
The guy wire is exactly
feet long.
(Type an exact answer, using radicals as needed.)
Part 2
The guy wire is approximatelyfeet long.
(Round to the nearest thousandth.)
Question 6
Not yet
answered
Marked out of
5.00
Flag question
=
If (4,6,-11) and (-12,-16,4),
=
Compute the cross product vx w
k
Consider the following vector field v^-> (x,y):
v^->(x,y)=2yi−xj
What is the magnitude of the vector v⃗ located in point (13,9)?
[Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places]
Chapter 1 Solutions
College Algebra, Books a la Carte Edition Plus NEW MyMathLab -- Access Card Package (6th Edition)
Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Prob. 4CVCCh. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Prob. 6CVCCh. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Prob. 8CVCCh. 1.1 - Prob. 1PECh. 1.1 - In Exercises 112, plot the given point in a...
Ch. 1.1 - Prob. 3PECh. 1.1 - Prob. 4PECh. 1.1 - Prob. 5PECh. 1.1 - Prob. 6PECh. 1.1 - In Exercises 112, plot the given point in a...Ch. 1.1 - Prob. 8PECh. 1.1 - In Exercises 112, plot the given point in a...Ch. 1.1 - In Exercises 112, plot the given point in a...Ch. 1.1 - Prob. 11PECh. 1.1 - Prob. 12PECh. 1.1 - Prob. 13PECh. 1.1 - Graph each equation in Exercises 1328. Let x = 3,...Ch. 1.1 - Graph each equation in Exercises 1328. Let x = 3,...Ch. 1.1 - Graph each equation in Exercises 1328. Let x = 3,...Ch. 1.1 - Prob. 17PECh. 1.1 - Graph each equation in Exercises 1328. Let x = 3,...Ch. 1.1 - Graph each equation in Exercises 1328. Let x = 3,...Ch. 1.1 - Prob. 20PECh. 1.1 - Prob. 21PECh. 1.1 - Prob. 22PECh. 1.1 - Prob. 23PECh. 1.1 - Prob. 24PECh. 1.1 - Prob. 25PECh. 1.1 - Prob. 26PECh. 1.1 - Prob. 27PECh. 1.1 - Prob. 28PECh. 1.1 - Prob. 29PECh. 1.1 - Prob. 30PECh. 1.1 - Prob. 31PECh. 1.1 - In Exercises 29 match the viewing rectangle with...Ch. 1.1 - Prob. 33PECh. 1.1 - Prob. 34PECh. 1.1 - Prob. 35PECh. 1.1 - Prob. 36PECh. 1.1 - Prob. 37PECh. 1.1 - Prob. 38PECh. 1.1 - Prob. 39PECh. 1.1 - Prob. 40PECh. 1.1 - Prob. 41PECh. 1.1 - Prob. 42PECh. 1.1 - Prob. 43PECh. 1.1 - Prob. 44PECh. 1.1 - Prob. 45PECh. 1.1 - Prob. 46PECh. 1.1 - Practice Plus In Exercises #x2013;50, write each...Ch. 1.1 - Prob. 48PECh. 1.1 - Practice Plus In Exercises 4750, write each...Ch. 1.1 - Prob. 50PECh. 1.1 - Prob. 51PECh. 1.1 - Prob. 52PECh. 1.1 - Prob. 53PECh. 1.1 - Prob. 54PECh. 1.1 - Prob. 55PECh. 1.1 - Prob. 56PECh. 1.1 - Contrary to popular belief, older people do not...Ch. 1.1 - Contrary to popular belief, older people do not...Ch. 1.1 - Prob. 59PECh. 1.1 - Prob. 60PECh. 1.1 - Prob. 61PECh. 1.1 - Prob. 62PECh. 1.1 - Prob. 63PECh. 1.1 - Prob. 64PECh. 1.1 - Prob. 65PECh. 1.1 - Technology Exercise Use a graphing utility to...Ch. 1.1 - Make Sense? In Exercises #x2013;70, determine...Ch. 1.1 - Prob. 68PECh. 1.1 - Prob. 69PECh. 1.1 - Prob. 70PECh. 1.1 - Prob. 71PECh. 1.1 - Prob. 72PECh. 1.1 - Prob. 73PECh. 1.1 - Prob. 74PECh. 1.1 - Prob. 75PECh. 1.1 - Prob. 76PECh. 1.1 - In Exercises 7578, list the quadrant or quadrants...Ch. 1.1 - In Exercises 75 list the quadrant or quadrants...Ch. 1.1 - Prob. 79PECh. 1.1 - Prob. 80PECh. 1.1 - Prob. 81PECh. 1.1 - Prob. 82PECh. 1.1 - Prob. 83PECh. 1.1 - Prob. 84PECh. 1.1 - Prob. 85PECh. 1.1 - Prob. 86PECh. 1.1 - Exercises 87#x2013;89 will help you prepare for...Ch. 1.1 - Prob. 88PECh. 1.1 - Exercises 87will help you prepare for the material...Ch. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Prob. 2CVCCh. 1.2 - Prob. 3CVCCh. 1.2 - Prob. 4CVCCh. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Prob. 6CVCCh. 1.2 - Prob. 7CVCCh. 1.2 - Prob. 8CVCCh. 1.2 - Prob. 9CVCCh. 1.2 - Prob. 10CVCCh. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Prob. 1PECh. 1.2 - Prob. 2PECh. 1.2 - Prob. 3PECh. 1.2 - Prob. 4PECh. 1.2 - Prob. 5PECh. 1.2 - Prob. 6PECh. 1.2 - Prob. 7PECh. 1.2 - Prob. 8PECh. 1.2 - Prob. 9PECh. 1.2 - Prob. 10PECh. 1.2 - In Exercises 116, solve and check each linear...Ch. 1.2 - Prob. 12PECh. 1.2 - Prob. 13PECh. 1.2 - Prob. 14PECh. 1.2 - Prob. 15PECh. 1.2 - Prob. 16PECh. 1.2 - Prob. 17PECh. 1.2 - Exercises 1730 contain linear equations with...Ch. 1.2 - Exercises 1730 contain linear equations with...Ch. 1.2 - Exercises 1730 contain linear equations with...Ch. 1.2 - Prob. 21PECh. 1.2 - Prob. 22PECh. 1.2 - Prob. 23PECh. 1.2 - Prob. 24PECh. 1.2 - Prob. 25PECh. 1.2 - Prob. 26PECh. 1.2 - Prob. 27PECh. 1.2 - Prob. 28PECh. 1.2 - Prob. 29PECh. 1.2 - Prob. 30PECh. 1.2 - Prob. 31PECh. 1.2 - Prob. 32PECh. 1.2 - Prob. 33PECh. 1.2 - Prob. 34PECh. 1.2 - Prob. 35PECh. 1.2 - Prob. 36PECh. 1.2 - Prob. 37PECh. 1.2 - Prob. 38PECh. 1.2 - Prob. 39PECh. 1.2 - Prob. 40PECh. 1.2 - Exercises 3150 contain rational equations with...Ch. 1.2 - Exercises 3150 contain rational equations with...Ch. 1.2 - Prob. 43PECh. 1.2 - Exercises 3150 contain rational equations with...Ch. 1.2 - Prob. 45PECh. 1.2 - Prob. 46PECh. 1.2 - Prob. 47PECh. 1.2 - Prob. 48PECh. 1.2 - Prob. 49PECh. 1.2 - Prob. 50PECh. 1.2 - Prob. 51PECh. 1.2 - Prob. 52PECh. 1.2 - Prob. 53PECh. 1.2 - Prob. 54PECh. 1.2 - Prob. 55PECh. 1.2 - Prob. 56PECh. 1.2 - Prob. 57PECh. 1.2 - Prob. 58PECh. 1.2 - Prob. 59PECh. 1.2 - Prob. 60PECh. 1.2 - Prob. 61PECh. 1.2 - Prob. 62PECh. 1.2 - Prob. 63PECh. 1.2 - Prob. 64PECh. 1.2 - Prob. 65PECh. 1.2 - Prob. 66PECh. 1.2 - Prob. 67PECh. 1.2 - Prob. 68PECh. 1.2 - Prob. 69PECh. 1.2 - Prob. 70PECh. 1.2 - Prob. 71PECh. 1.2 - Prob. 72PECh. 1.2 - Prob. 73PECh. 1.2 - Prob. 74PECh. 1.2 - Prob. 75PECh. 1.2 - Prob. 76PECh. 1.2 - Prob. 77PECh. 1.2 - Prob. 78PECh. 1.2 - Prob. 79PECh. 1.2 - Prob. 80PECh. 1.2 - Prob. 81PECh. 1.2 - Prob. 82PECh. 1.2 - Prob. 83PECh. 1.2 - Prob. 84PECh. 1.2 - Prob. 85PECh. 1.2 - Prob. 86PECh. 1.2 - Prob. 87PECh. 1.2 - Prob. 88PECh. 1.2 - Prob. 89PECh. 1.2 - Prob. 90PECh. 1.2 - Prob. 91PECh. 1.2 - Prob. 92PECh. 1.2 - Prob. 93PECh. 1.2 - Prob. 94PECh. 1.2 - Prob. 95PECh. 1.2 - Prob. 96PECh. 1.2 - Application Exercises
In the year after warning...Ch. 1.2 - Application Exercises In the years after warning...Ch. 1.2 - The line graph shows the cost of inflation. What...Ch. 1.2 - The line graph shows the cost of inflation. What...Ch. 1.2 - Prob. 101PECh. 1.2 - The line graph shows the cost of inflation. What...Ch. 1.2 - Prob. 103PECh. 1.2 - Prob. 104PECh. 1.2 - Prob. 105PECh. 1.2 - Prob. 106PECh. 1.2 - Prob. 107PECh. 1.2 - Prob. 108PECh. 1.2 - Prob. 109PECh. 1.2 - Prob. 110PECh. 1.2 - Prob. 111PECh. 1.2 - Prob. 112PECh. 1.2 - Prob. 113PECh. 1.2 - Prob. 114PECh. 1.2 - Prob. 115PECh. 1.2 - Prob. 116PECh. 1.2 - Prob. 117PECh. 1.2 - Prob. 118PECh. 1.2 - Prob. 119PECh. 1.2 - Prob. 120PECh. 1.2 - Prob. 121PECh. 1.2 - Prob. 122PECh. 1.2 - Prob. 123PECh. 1.2 - Prob. 124PECh. 1.2 - Prob. 125PECh. 1.2 - In Exercises 124127, determine whether each...Ch. 1.2 - Prob. 127PECh. 1.2 - Prob. 128PECh. 1.2 - Prob. 129PECh. 1.2 - Find b such that 4xbx5=3 has a solution set given...Ch. 1.2 - Prob. 131PECh. 1.2 - Prob. 132PECh. 1.2 - Preview Exercises Exercise 131will help you...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Prob. 1PECh. 1.3 - Prob. 2PECh. 1.3 - Prob. 3PECh. 1.3 - Prob. 4PECh. 1.3 - Use the five-step strategy for solving word...Ch. 1.3 - Prob. 6PECh. 1.3 - Prob. 7PECh. 1.3 - Prob. 8PECh. 1.3 - Prob. 9PECh. 1.3 - Use the five-step strategy for solving word...Ch. 1.3 - Prob. 11PECh. 1.3 - In Exercises 1118, find all values of x satisfying...Ch. 1.3 - In Exercises 1118, find all value of x satisfying...Ch. 1.3 - Prob. 14PECh. 1.3 - Prob. 15PECh. 1.3 - Prob. 16PECh. 1.3 - Prob. 17PECh. 1.3 - Prob. 18PECh. 1.3 - How will you spend your average life expectancy of...Ch. 1.3 - How will you spend your average life expectancy of...Ch. 1.3 - Prob. 21PECh. 1.3 - Prob. 22PECh. 1.3 - Prob. 23PECh. 1.3 - Even as Americans increasingly view a college...Ch. 1.3 - A new car worth $24,000 is depreciating in value...Ch. 1.3 - Prob. 26PECh. 1.3 - You are choosing between two health clubs. Club A...Ch. 1.3 - You need to rent a rug cleaner. Company A will...Ch. 1.3 - Prob. 29PECh. 1.3 - A discount pass for a bridge costs $30 per month....Ch. 1.3 - In 2010, there were 13,300 students at college A....Ch. 1.3 - Prob. 32PECh. 1.3 - Prob. 33PECh. 1.3 - Prob. 34PECh. 1.3 - Prob. 35PECh. 1.3 - Prob. 36PECh. 1.3 - Prob. 37PECh. 1.3 - Exercises 1920 involve markup, the amount added to...Ch. 1.3 - Prob. 39PECh. 1.3 - Prob. 40PECh. 1.3 - Prob. 41PECh. 1.3 - Prob. 42PECh. 1.3 - Prob. 43PECh. 1.3 - Prob. 44PECh. 1.3 - Prob. 45PECh. 1.3 - Prob. 46PECh. 1.3 - Prob. 47PECh. 1.3 - Prob. 48PECh. 1.3 - Prob. 49PECh. 1.3 - Prob. 50PECh. 1.3 - Prob. 51PECh. 1.3 - Prob. 52PECh. 1.3 - Answer the question in the following Peanuts...Ch. 1.3 - Prob. 54PECh. 1.3 - Prob. 55PECh. 1.3 - Prob. 56PECh. 1.3 - In Exercises 3756, solve each formula for the...Ch. 1.3 - Prob. 58PECh. 1.3 - Prob. 59PECh. 1.3 - Prob. 60PECh. 1.3 - Prob. 61PECh. 1.3 - Prob. 62PECh. 1.3 - Prob. 63PECh. 1.3 - Prob. 64PECh. 1.3 - Prob. 65PECh. 1.3 - Prob. 66PECh. 1.3 - Prob. 67PECh. 1.3 - Prob. 68PECh. 1.3 - Prob. 69PECh. 1.3 - Prob. 70PECh. 1.3 - Prob. 71PECh. 1.3 - Prob. 72PECh. 1.3 - Prob. 73PECh. 1.3 - In Exercises 37 solve each formula for the...Ch. 1.3 - Prob. 75PECh. 1.3 - Prob. 76PECh. 1.3 - Prob. 77PECh. 1.3 - Prob. 78PECh. 1.3 - Prob. 79PECh. 1.3 - Prob. 80PECh. 1.3 - Make Sense? In Exercises 81–84, determine whether...Ch. 1.3 - Prob. 82PECh. 1.3 - Prob. 83PECh. 1.3 - Prob. 84PECh. 1.3 - Prob. 85PECh. 1.3 - Prob. 86PECh. 1.3 - Prob. 87PECh. 1.3 - Prob. 88PECh. 1.3 - Prob. 89PECh. 1.3 - Prob. 90PECh. 1.3 - Prob. 91PECh. 1.3 - One of the best ways to learn how to solve a word...Ch. 1.3 - Exercises #x2013;77 will help you prepare for the...Ch. 1.3 - Prob. 94PECh. 1.3 - Exercises 75will help you prepare for the material...Ch. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Prob. 4CVCCh. 1.4 - Prob. 5CVCCh. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Prob. 7CVCCh. 1.4 - Prob. 8CVCCh. 1.4 - In Exercises 18, add or subtract as indicated and...Ch. 1.4 - In Exercises 18, add or subtract as indicated and...Ch. 1.4 - Prob. 3PECh. 1.4 - Prob. 4PECh. 1.4 - Prob. 5PECh. 1.4 - In Exercises 18, add or subtract as indicated and...Ch. 1.4 - Prob. 7PECh. 1.4 - Prob. 8PECh. 1.4 - Prob. 9PECh. 1.4 - Prob. 10PECh. 1.4 - Prob. 11PECh. 1.4 - Prob. 12PECh. 1.4 - Prob. 13PECh. 1.4 - Prob. 14PECh. 1.4 - Prob. 15PECh. 1.4 - Prob. 16PECh. 1.4 - Prob. 17PECh. 1.4 - Prob. 18PECh. 1.4 - In Exercises 920, find each product and write the...Ch. 1.4 - Prob. 20PECh. 1.4 - In Exercises #x2013;28, divide and express the...Ch. 1.4 - Prob. 22PECh. 1.4 - Prob. 23PECh. 1.4 - Prob. 24PECh. 1.4 - Prob. 25PECh. 1.4 - Prob. 26PECh. 1.4 - Prob. 27PECh. 1.4 - Prob. 28PECh. 1.4 - Prob. 29PECh. 1.4 - Prob. 30PECh. 1.4 - Prob. 31PECh. 1.4 - Prob. 32PECh. 1.4 - Prob. 33PECh. 1.4 - Prob. 34PECh. 1.4 - Prob. 35PECh. 1.4 - Prob. 36PECh. 1.4 - Prob. 37PECh. 1.4 - Prob. 38PECh. 1.4 - Prob. 39PECh. 1.4 - Prob. 40PECh. 1.4 - Prob. 41PECh. 1.4 - Prob. 42PECh. 1.4 - Prob. 43PECh. 1.4 - Prob. 44PECh. 1.4 - Prob. 45PECh. 1.4 - Prob. 46PECh. 1.4 - Prob. 47PECh. 1.4 - Prob. 48PECh. 1.4 - Prob. 49PECh. 1.4 - In Exercises 45 perform the indicated operation(s)...Ch. 1.4 - Prob. 51PECh. 1.4 - Prob. 52PECh. 1.4 - Prob. 53PECh. 1.4 - Prob. 54PECh. 1.4 - Prob. 55PECh. 1.4 - Prob. 56PECh. 1.4 - Prob. 57PECh. 1.4 - Prob. 58PECh. 1.4 - Prob. 59PECh. 1.4 - Prob. 60PECh. 1.4 - Prob. 61PECh. 1.4 - Prob. 62PECh. 1.4 - Explain each of the three jokes in the cartoon on...Ch. 1.4 - Prob. 64PECh. 1.4 - Prob. 65PECh. 1.4 - Prob. 66PECh. 1.4 - Prob. 67PECh. 1.4 - Prob. 68PECh. 1.4 - Prob. 69PECh. 1.4 - Prob. 70PECh. 1.4 - Prob. 71PECh. 1.4 - Prob. 72PECh. 1.4 - Prob. 73PECh. 1.4 - Prob. 74PECh. 1.4 - Prob. 75PECh. 1.4 - Prob. 76PECh. 1.4 - Prob. 77PECh. 1.4 - Prob. 78PECh. 1.4 - Prob. 79PECh. 1.4 - Prob. 80PECh. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Fill in each blank so that the resulting statement...Ch. 1.5 - Prob. 13CVCCh. 1.5 - Prob. 14CVCCh. 1.5 - Prob. 15CVCCh. 1.5 - Prob. 16CVCCh. 1.5 - Prob. 17CVCCh. 1.5 - Prob. 18CVCCh. 1.5 - Prob. 19CVCCh. 1.5 - Prob. 20CVCCh. 1.5 - Prob. 21CVCCh. 1.5 - Prob. 22CVCCh. 1.5 - Prob. 1PECh. 1.5 - Prob. 2PECh. 1.5 - Prob. 3PECh. 1.5 - Prob. 4PECh. 1.5 - Prob. 5PECh. 1.5 - Prob. 6PECh. 1.5 - Prob. 7PECh. 1.5 - Prob. 8PECh. 1.5 - Prob. 9PECh. 1.5 - Prob. 10PECh. 1.5 - Prob. 11PECh. 1.5 - Prob. 12PECh. 1.5 - Prob. 13PECh. 1.5 - Prob. 14PECh. 1.5 - Prob. 15PECh. 1.5 - Prob. 16PECh. 1.5 - Prob. 17PECh. 1.5 - Prob. 18PECh. 1.5 - Prob. 19PECh. 1.5 - Prob. 20PECh. 1.5 - Prob. 21PECh. 1.5 - Solve each equation in Exercises 1534 by the...Ch. 1.5 - Prob. 23PECh. 1.5 - Prob. 24PECh. 1.5 - Prob. 25PECh. 1.5 - Prob. 26PECh. 1.5 - Prob. 27PECh. 1.5 - Prob. 28PECh. 1.5 - Prob. 29PECh. 1.5 - Prob. 30PECh. 1.5 - Prob. 31PECh. 1.5 - Prob. 32PECh. 1.5 - Prob. 33PECh. 1.5 - Prob. 34PECh. 1.5 - Prob. 35PECh. 1.5 - In Exercises 3546, determine the constant that...Ch. 1.5 - Prob. 37PECh. 1.5 - Prob. 38PECh. 1.5 - Prob. 39PECh. 1.5 - Prob. 40PECh. 1.5 - Prob. 41PECh. 1.5 - Prob. 42PECh. 1.5 - Prob. 43PECh. 1.5 - Prob. 44PECh. 1.5 - Prob. 45PECh. 1.5 - Prob. 46PECh. 1.5 - Prob. 47PECh. 1.5 - Prob. 48PECh. 1.5 - Prob. 49PECh. 1.5 - Prob. 50PECh. 1.5 - Prob. 51PECh. 1.5 - Prob. 52PECh. 1.5 - Prob. 53PECh. 1.5 - Prob. 54PECh. 1.5 - Prob. 55PECh. 1.5 - Prob. 56PECh. 1.5 - Prob. 57PECh. 1.5 - Prob. 58PECh. 1.5 - Prob. 59PECh. 1.5 - Prob. 60PECh. 1.5 - Prob. 61PECh. 1.5 - Prob. 62PECh. 1.5 - Prob. 63PECh. 1.5 - Prob. 64PECh. 1.5 - Prob. 65PECh. 1.5 - Prob. 66PECh. 1.5 - Prob. 67PECh. 1.5 - Prob. 68PECh. 1.5 - Prob. 69PECh. 1.5 - Prob. 70PECh. 1.5 - Prob. 71PECh. 1.5 - Solve each equation in Exercises 6574 using the...Ch. 1.5 - Prob. 73PECh. 1.5 - Prob. 74PECh. 1.5 - Prob. 75PECh. 1.5 - Prob. 76PECh. 1.5 - Prob. 77PECh. 1.5 - Prob. 78PECh. 1.5 - Prob. 79PECh. 1.5 - Prob. 80PECh. 1.5 - Prob. 81PECh. 1.5 - Prob. 82PECh. 1.5 - Prob. 83PECh. 1.5 - Prob. 84PECh. 1.5 - Prob. 85PECh. 1.5 - Prob. 86PECh. 1.5 - Prob. 87PECh. 1.5 - Prob. 88PECh. 1.5 - Prob. 89PECh. 1.5 - Prob. 90PECh. 1.5 - Prob. 91PECh. 1.5 - Prob. 92PECh. 1.5 - Prob. 93PECh. 1.5 - Prob. 94PECh. 1.5 - Prob. 95PECh. 1.5 - Prob. 96PECh. 1.5 - Prob. 97PECh. 1.5 - Solve each equation in Exercises 83108 by the...Ch. 1.5 - Prob. 99PECh. 1.5 - Prob. 100PECh. 1.5 - Prob. 101PECh. 1.5 - Prob. 102PECh. 1.5 - Prob. 103PECh. 1.5 - Prob. 104PECh. 1.5 - Prob. 105PECh. 1.5 - Prob. 106PECh. 1.5 - Prob. 107PECh. 1.5 - Prob. 108PECh. 1.5 - Prob. 109PECh. 1.5 - Prob. 110PECh. 1.5 - Prob. 111PECh. 1.5 - Prob. 112PECh. 1.5 - Prob. 113PECh. 1.5 - Prob. 114PECh. 1.5 - Prob. 115PECh. 1.5 - Prob. 116PECh. 1.5 - Prob. 117PECh. 1.5 - Prob. 118PECh. 1.5 - Prob. 119PECh. 1.5 - Prob. 120PECh. 1.5 - Prob. 121PECh. 1.5 - Prob. 122PECh. 1.5 - Prob. 123PECh. 1.5 - In Exercises 123 list all number that must be...Ch. 1.5 - Prob. 125PECh. 1.5 - Prob. 126PECh. 1.5 - Prob. 127PECh. 1.5 - In Exercises 127130, solve each equation by the...Ch. 1.5 - Prob. 129PECh. 1.5 - Prob. 130PECh. 1.5 - Prob. 131PECh. 1.5 - Prob. 132PECh. 1.5 - Prob. 133PECh. 1.5 - Prob. 134PECh. 1.5 - A drivers age has something to do with his or her...Ch. 1.5 - A drivers age has something to do with his or her...Ch. 1.5 - Throwing events in track and field include the...Ch. 1.5 - Throwing events in track and field include the...Ch. 1.5 - Prob. 139PECh. 1.5 - Prob. 140PECh. 1.5 - Prob. 141PECh. 1.5 - Prob. 142PECh. 1.5 - Prob. 143PECh. 1.5 - Prob. 144PECh. 1.5 - Prob. 145PECh. 1.5 - Prob. 146PECh. 1.5 - Prob. 147PECh. 1.5 - Prob. 148PECh. 1.5 - Prob. 149PECh. 1.5 - Prob. 150PECh. 1.5 - Prob. 151PECh. 1.5 - Prob. 152PECh. 1.5 - A rain gutter is made from sheets of aluminum that...Ch. 1.5 - Prob. 154PECh. 1.5 - Prob. 155PECh. 1.5 - Prob. 156PECh. 1.5 - Prob. 157PECh. 1.5 - Prob. 158PECh. 1.5 - Prob. 159PECh. 1.5 - Prob. 160PECh. 1.5 - Prob. 161PECh. 1.5 - Prob. 162PECh. 1.5 - Prob. 163PECh. 1.5 - Prob. 164PECh. 1.5 - Prob. 165PECh. 1.5 - Prob. 166PECh. 1.5 - Prob. 167PECh. 1.5 - Prob. 168PECh. 1.5 - Prob. 169PECh. 1.5 - Prob. 170PECh. 1.5 - Prob. 171PECh. 1.5 - Prob. 172PECh. 1.5 - Prob. 173PECh. 1.5 - Prob. 174PECh. 1.5 - Prob. 175PECh. 1.5 - Prob. 176PECh. 1.5 - Prob. 177PECh. 1.5 - Prob. 178PECh. 1.5 - Prob. 179PECh. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Prob. 6CVCCh. 1.6 - Prob. 7CVCCh. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Prob. 9CVCCh. 1.6 - Prob. 10CVCCh. 1.6 - Prob. 11CVCCh. 1.6 - Solve each polynomial equation in Exercises 110 by...Ch. 1.6 - Solve each polynomial equation in Exercises 110 by...Ch. 1.6 - Prob. 3PECh. 1.6 - Prob. 4PECh. 1.6 - Prob. 5PECh. 1.6 - Solve each polynomial equation in Exercises 110 by...Ch. 1.6 - Prob. 7PECh. 1.6 - Prob. 8PECh. 1.6 - Prob. 9PECh. 1.6 - Prob. 10PECh. 1.6 - Prob. 11PECh. 1.6 - Prob. 12PECh. 1.6 - Prob. 13PECh. 1.6 - Prob. 14PECh. 1.6 - Prob. 15PECh. 1.6 - Prob. 16PECh. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Prob. 18PECh. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Prob. 20PECh. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Prob. 24PECh. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Prob. 26PECh. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Prob. 28PECh. 1.6 - Solve each radical equation in Exercises 1130....Ch. 1.6 - Prob. 30PECh. 1.6 - Solve each equation with rational exponents in...Ch. 1.6 - Prob. 32PECh. 1.6 - Prob. 33PECh. 1.6 - Solve each equation with rational exponents in...Ch. 1.6 - Prob. 35PECh. 1.6 - Solve each equation with rational exponents in...Ch. 1.6 - Prob. 37PECh. 1.6 - Solve each equation with rational exponents in...Ch. 1.6 - Prob. 39PECh. 1.6 - Solve each equation with rational exponents in...Ch. 1.6 - Prob. 41PECh. 1.6 - Prob. 42PECh. 1.6 - Prob. 43PECh. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Prob. 48PECh. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Prob. 53PECh. 1.6 - Prob. 54PECh. 1.6 - Prob. 55PECh. 1.6 - Solve each equation in Exercises 4160 by making an...Ch. 1.6 - Prob. 57PECh. 1.6 - Prob. 58PECh. 1.6 - Prob. 59PECh. 1.6 - Prob. 60PECh. 1.6 - Prob. 61PECh. 1.6 - Prob. 62PECh. 1.6 - Prob. 63PECh. 1.6 - Prob. 64PECh. 1.6 - In Exercises 6178, solve each absolute value...Ch. 1.6 - Prob. 66PECh. 1.6 - Prob. 67PECh. 1.6 - Prob. 68PECh. 1.6 - Prob. 69PECh. 1.6 - Prob. 70PECh. 1.6 - Prob. 71PECh. 1.6 - In Exercises 6178, solve each absolute value...Ch. 1.6 - Prob. 73PECh. 1.6 - Prob. 74PECh. 1.6 - Prob. 75PECh. 1.6 - Prob. 76PECh. 1.6 - In Exercises 6178, solve each absolute value...Ch. 1.6 - In Exercises 61 solve each absolute value equation...Ch. 1.6 - Prob. 79PECh. 1.6 - Prob. 80PECh. 1.6 - In Exercises 7984, find the x-intercepts of the...Ch. 1.6 - In Exercises 7984, find the x-intercepts of the...Ch. 1.6 - In Exercises 7984, find the x-intercepts of the...Ch. 1.6 - In Exercises 79 find the x-intercepts of the graph...Ch. 1.6 - In Exercises #x2013;94, find all values of x...Ch. 1.6 - In Exercises 8594, find all values of x satisfying...Ch. 1.6 - In Exercises 8594, find all values of x satisfying...Ch. 1.6 - In Exercises 8594, find all values of x satisfying...Ch. 1.6 - In Exercises 8594, find all values of x satisfying...Ch. 1.6 - Prob. 90PECh. 1.6 - Prob. 91PECh. 1.6 - Prob. 92PECh. 1.6 - In Exercises 8594, find all values of x satisfying...Ch. 1.6 - In Exercises 85 find all values of x satisfying...Ch. 1.6 - In Exercises #x2013;98, solve each equation. |x2 +...Ch. 1.6 - Prob. 96PECh. 1.6 - Prob. 97PECh. 1.6 - In Exercises 9598, solve each equation. x(x 2)3 ...Ch. 1.6 - If 5 times a number is decreased by 4, the...Ch. 1.6 - If a number is decreased by 3, the principal...Ch. 1.6 - Solve for V:r=3Vh.Ch. 1.6 - Solve for A:r=A4.Ch. 1.6 - In Exercises #x2013;104, list all numbers that...Ch. 1.6 - In Exercises 103 list all numbers that must be...Ch. 1.6 - Prob. 105PECh. 1.6 - Prob. 106PECh. 1.6 - Use the graph of the formula for hang time to...Ch. 1.6 - Use the graph of the formula for hang time to...Ch. 1.6 - Prob. 109PECh. 1.6 - Prob. 110PECh. 1.6 - For each planet in our solar system, its year is...Ch. 1.6 - For each planet in your in our solar system, its...Ch. 1.6 - Use the Pythagorean Theorem to solve Exercises...Ch. 1.6 - Use the Pythagorean Theorem to solve Exercises 113...Ch. 1.6 - Without actually solving the equation, give a...Ch. 1.6 - Prob. 116PECh. 1.6 - What is an extraneous solution to a radical...Ch. 1.6 - Explain how to recognize an equation that is...Ch. 1.6 - Describe two methods for solving this equation:...Ch. 1.6 - Explain how to solve an equation involving...Ch. 1.6 - Prob. 121PECh. 1.6 - Prob. 122PECh. 1.6 - Prob. 123PECh. 1.6 - Prob. 124PECh. 1.6 - Prob. 125PECh. 1.6 - Prob. 126PECh. 1.6 - Prob. 127PECh. 1.6 - Make Sense? In Exercises 125 determine whether...Ch. 1.6 - Prob. 129PECh. 1.6 - Prob. 130PECh. 1.6 - Prob. 131PECh. 1.6 - Prob. 132PECh. 1.6 - Prob. 133PECh. 1.6 - Solve without squaring both sides: 52x=52x.Ch. 1.6 - Prob. 135PECh. 1.6 - Prob. 136PECh. 1.6 - Exercises #x2013;139 will help you prepare for the...Ch. 1.6 - Exercises 137139 will help you prepare for the...Ch. 1.6 - Exercises 137will help you prepare for the...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Prob. 11CVCCh. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Fill in each blank so that the resulting statement...Ch. 1.7 - Prob. 1PECh. 1.7 - Prob. 2PECh. 1.7 - Prob. 3PECh. 1.7 - Prob. 4PECh. 1.7 - Prob. 5PECh. 1.7 - Prob. 6PECh. 1.7 - In Exercises 114, express each interval in...Ch. 1.7 - Prob. 8PECh. 1.7 - Prob. 9PECh. 1.7 - Prob. 10PECh. 1.7 - Prob. 11PECh. 1.7 - In Exercises 114, express each interval in...Ch. 1.7 - In Exercises 1, express each interval in...Ch. 1.7 - Prob. 14PECh. 1.7 - Prob. 15PECh. 1.7 - Prob. 16PECh. 1.7 - Prob. 17PECh. 1.7 - Prob. 18PECh. 1.7 - Prob. 19PECh. 1.7 - In Exercises 1526, use graphs to find each set....Ch. 1.7 - Prob. 21PECh. 1.7 - Prob. 22PECh. 1.7 - Prob. 23PECh. 1.7 - Prob. 24PECh. 1.7 - Prob. 25PECh. 1.7 - Prob. 26PECh. 1.7 - Prob. 27PECh. 1.7 - Prob. 28PECh. 1.7 - Prob. 29PECh. 1.7 - Prob. 30PECh. 1.7 - Prob. 31PECh. 1.7 - Prob. 32PECh. 1.7 - Prob. 33PECh. 1.7 - Prob. 34PECh. 1.7 - Prob. 35PECh. 1.7 - Prob. 36PECh. 1.7 - Prob. 37PECh. 1.7 - Prob. 38PECh. 1.7 - Prob. 39PECh. 1.7 - Prob. 40PECh. 1.7 - Prob. 41PECh. 1.7 - Prob. 42PECh. 1.7 - Prob. 43PECh. 1.7 - Prob. 44PECh. 1.7 - Prob. 45PECh. 1.7 - Prob. 46PECh. 1.7 - Prob. 47PECh. 1.7 - Prob. 48PECh. 1.7 - Prob. 49PECh. 1.7 - Prob. 50PECh. 1.7 - Prob. 51PECh. 1.7 - Prob. 52PECh. 1.7 - Prob. 53PECh. 1.7 - Prob. 54PECh. 1.7 - Prob. 55PECh. 1.7 - Prob. 56PECh. 1.7 - Prob. 57PECh. 1.7 - Prob. 58PECh. 1.7 - Prob. 59PECh. 1.7 - Prob. 60PECh. 1.7 - Prob. 61PECh. 1.7 - Prob. 62PECh. 1.7 - Prob. 63PECh. 1.7 - Prob. 64PECh. 1.7 - Prob. 65PECh. 1.7 - Prob. 66PECh. 1.7 - Prob. 67PECh. 1.7 - Prob. 68PECh. 1.7 - Prob. 69PECh. 1.7 - Prob. 70PECh. 1.7 - Prob. 71PECh. 1.7 - Prob. 72PECh. 1.7 - Prob. 73PECh. 1.7 - Prob. 74PECh. 1.7 - Prob. 75PECh. 1.7 - Prob. 76PECh. 1.7 - Prob. 77PECh. 1.7 - Prob. 78PECh. 1.7 - Prob. 79PECh. 1.7 - Prob. 80PECh. 1.7 - Prob. 81PECh. 1.7 - Prob. 82PECh. 1.7 - Prob. 83PECh. 1.7 - Prob. 84PECh. 1.7 - Prob. 85PECh. 1.7 - Prob. 86PECh. 1.7 - Prob. 87PECh. 1.7 - Prob. 88PECh. 1.7 - Prob. 89PECh. 1.7 - Prob. 90PECh. 1.7 - In all exercises, other than , use interval...Ch. 1.7 - Prob. 92PECh. 1.7 - Prob. 93PECh. 1.7 - Prob. 94PECh. 1.7 - Prob. 95PECh. 1.7 - Prob. 96PECh. 1.7 - Prob. 97PECh. 1.7 - Prob. 98PECh. 1.7 - Prob. 99PECh. 1.7 - Prob. 100PECh. 1.7 - Prob. 101PECh. 1.7 - Prob. 102PECh. 1.7 - Prob. 103PECh. 1.7 - Prob. 104PECh. 1.7 - Prob. 105PECh. 1.7 - Prob. 106PECh. 1.7 - Prob. 107PECh. 1.7 - Prob. 108PECh. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - Prob. 114PECh. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - The graphs show that the three components of love,...Ch. 1.7 - Prob. 117PECh. 1.7 - Prob. 118PECh. 1.7 - Prob. 119PECh. 1.7 - Prob. 120PECh. 1.7 - If a coin tossed 100 times, we would expect...Ch. 1.7 - Prob. 122PECh. 1.7 - Prob. 123PECh. 1.7 - In Exercises 122133, use the strategy for solving...Ch. 1.7 - Prob. 125PECh. 1.7 - Prob. 126PECh. 1.7 - Prob. 127PECh. 1.7 - In Exercises 122133, use the strategy for solving...Ch. 1.7 - In Exercises 122123, use the strategy for solving...Ch. 1.7 - Prob. 130PECh. 1.7 - Prob. 131PECh. 1.7 - In Exercises 122133, use the strategy for solving...Ch. 1.7 - Prob. 133PECh. 1.7 - Prob. 134PECh. 1.7 - Describe ways in which solving a linear inequality...Ch. 1.7 - Prob. 136PECh. 1.7 - Prob. 137PECh. 1.7 - Prob. 138PECh. 1.7 - Prob. 139PECh. 1.7 - Explain why |x| 4 has no solution.Ch. 1.7 - Describe the solution set of |x| 4.Ch. 1.7 - In Exercises #x2013;143, solve each inequality...Ch. 1.7 - In Exercises 142 solve each inequality using a...Ch. 1.7 - Prob. 144PECh. 1.7 - Prob. 145PECh. 1.7 - Critical Thinking Exercises Make Sense? In...Ch. 1.7 - Critical Thinking Exercises Make Sense? In...Ch. 1.7 - Critical Thinking Exercises Make Sense? In...Ch. 1.7 - Critical Thinking Exercises Make Sense? In...Ch. 1.7 - In Exercises #x2013;153, determine whether each...Ch. 1.7 - In Exercises 150153, determine whether each...Ch. 1.7 - Prob. 152PECh. 1.7 - In Exercises 150 determine whether each statement...Ch. 1.7 - Whats wrong with this argument? Suppose x and y...Ch. 1.7 - Write an absolute value inequality for which the...Ch. 1.7 - Each group member should research one situation...Ch. 1.7 - Prob. 157PECh. 1.7 - Prob. 158PECh. 1.7 - Prob. 159PECh. 1 - In Exercises 112, solve each equation. 5 + 3(x +...Ch. 1 - In Exercises 112, solve each equation. 5x2 2x = 7Ch. 1 - Prob. 3MCCPCh. 1 - Prob. 4MCCPCh. 1 - Prob. 5MCCPCh. 1 - Prob. 6MCCPCh. 1 - Prob. 7MCCPCh. 1 - Prob. 8MCCPCh. 1 - Prob. 9MCCPCh. 1 - Prob. 10MCCPCh. 1 - Prob. 11MCCPCh. 1 - Prob. 12MCCPCh. 1 - Prob. 13MCCPCh. 1 - Prob. 14MCCPCh. 1 - Prob. 15MCCPCh. 1 - Prob. 16MCCPCh. 1 - Prob. 17MCCPCh. 1 - Prob. 18MCCPCh. 1 - Prob. 19MCCPCh. 1 - Prob. 20MCCPCh. 1 - Prob. 21MCCPCh. 1 - Prob. 22MCCPCh. 1 - Prob. 23MCCPCh. 1 - Prob. 24MCCPCh. 1 - Prob. 25MCCPCh. 1 - Prob. 26MCCPCh. 1 - Prob. 27MCCPCh. 1 - Solve for f1:f=f1f2f1+f2Ch. 1 - Prob. 29MCCPCh. 1 - Prob. 30MCCPCh. 1 - Prob. 31MCCPCh. 1 - Prob. 32MCCPCh. 1 - Prob. 33MCCPCh. 1 - Prob. 34MCCPCh. 1 - Prob. 35MCCPCh. 1 - Prob. 36MCCPCh. 1 - Prob. 37MCCPCh. 1 - a. The alligator, at one time an endangered...Ch. 1 - Prob. 39MCCPCh. 1 - Prob. 40MCCPCh. 1 - Prob. 41MCCPCh. 1 - Prob. 42MCCPCh. 1 - Prob. 43MCCPCh. 1 - Prob. 44MCCPCh. 1 - Prob. 45MCCPCh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Salary after College. In 2010, Monster College...Ch. 1 - Salary after College. In Monster College surveyed...Ch. 1 - Salary after College. In 2010, Monster College...Ch. 1 - Prob. 12RECh. 1 - Salary after College. In 2010, Monster College...Ch. 1 - Salary after College. In 2010, Monster College...Ch. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - In Exercises 1535, solve each equation. Then state...Ch. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - In Exercises 3643, use the five-step strategy for...Ch. 1 - The bar graph shows the average price of a movie...Ch. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - In Exercises 3643, use the five-step strategy for...Ch. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - In 2015, there were 14.100 students at college A....Ch. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Solve each equation in Exercises #x2013;59 by...Ch. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - 83. As gas prices surge, more Americans are...Ch. 1 - Prob. 84RECh. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - Prob. 89RECh. 1 - Prob. 90RECh. 1 - Solve the equations with rational exponents in...Ch. 1 - Prob. 92RECh. 1 - Prob. 93RECh. 1 - Prob. 94RECh. 1 - Prob. 95RECh. 1 - Prob. 96RECh. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 100RECh. 1 - Prob. 101RECh. 1 - Prob. 102RECh. 1 - Prob. 103RECh. 1 - Prob. 104RECh. 1 - Prob. 105RECh. 1 - Prob. 106RECh. 1 - Prob. 107RECh. 1 - Prob. 108RECh. 1 - Prob. 109RECh. 1 - Prob. 110RECh. 1 - Prob. 111RECh. 1 - Prob. 112RECh. 1 - Prob. 113RECh. 1 - Prob. 114RECh. 1 - Prob. 115RECh. 1 - Prob. 116RECh. 1 - Prob. 117RECh. 1 - Prob. 118RECh. 1 - Prob. 119RECh. 1 - In Exercises 111121, solve each inequality. Other...Ch. 1 - Prob. 121RECh. 1 - Prob. 122RECh. 1 - Prob. 123RECh. 1 - A car rental agency rents a certain car for $40...Ch. 1 - Prob. 125RECh. 1 - Prob. 126RECh. 1 - Prob. 1TCh. 1 - Prob. 2TCh. 1 - Prob. 3TCh. 1 - Prob. 4TCh. 1 - Prob. 5TCh. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Prob. 8TCh. 1 - Prob. 9TCh. 1 - Prob. 10TCh. 1 - Prob. 11TCh. 1 - Prob. 12TCh. 1 - Prob. 13TCh. 1 - Prob. 14TCh. 1 - Prob. 15TCh. 1 - Prob. 16TCh. 1 - Prob. 17TCh. 1 - Prob. 18TCh. 1 - Prob. 19TCh. 1 - Prob. 20TCh. 1 - Prob. 21TCh. 1 - Prob. 22TCh. 1 - Prob. 23TCh. 1 - Prob. 24TCh. 1 - Prob. 25TCh. 1 - Prob. 26TCh. 1 - Prob. 27TCh. 1 - Prob. 28TCh. 1 - Prob. 29TCh. 1 - In Exercises #x2013;31, graph each equation in a...Ch. 1 - Prob. 31TCh. 1 - Prob. 32TCh. 1 - Prob. 33TCh. 1 - Prob. 34TCh. 1 - Prob. 35TCh. 1 - Prob. 36TCh. 1 - Prob. 37TCh. 1 - Prob. 38TCh. 1 - Prob. 39TCh. 1 - Prob. 40TCh. 1 - Prob. 41TCh. 1 - Prob. 42TCh. 1 - Prob. 43TCh. 1 - You are choosing between two texting plans. Plan A...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Question 4 Find the value of the first element for the first row of the inverse matrix of matrix B. 3 Not yet answered B = Marked out of 5.00 · (³ ;) Flag question 7 [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places] Answer:arrow_forwardQuestion 2 Not yet answered Multiply the following Matrices together: [77-4 A = 36 Marked out of -5 -5 5.00 B = 3 5 Flag question -6 -7 ABarrow_forwardAssume {u1, U2, u3, u4} does not span R³. Select the best statement. A. {u1, U2, u3} spans R³ if u̸4 is a linear combination of other vectors in the set. B. We do not have sufficient information to determine whether {u₁, u2, u3} spans R³. C. {U1, U2, u3} spans R³ if u̸4 is a scalar multiple of another vector in the set. D. {u1, U2, u3} cannot span R³. E. {U1, U2, u3} spans R³ if u̸4 is the zero vector. F. none of the abovearrow_forward
- Select the best statement. A. If a set of vectors includes the zero vector 0, then the set of vectors can span R^ as long as the other vectors are distinct. n B. If a set of vectors includes the zero vector 0, then the set of vectors spans R precisely when the set with 0 excluded spans Rª. ○ C. If a set of vectors includes the zero vector 0, then the set of vectors can span Rn as long as it contains n vectors. ○ D. If a set of vectors includes the zero vector 0, then there is no reasonable way to determine if the set of vectors spans Rn. E. If a set of vectors includes the zero vector 0, then the set of vectors cannot span Rn. F. none of the abovearrow_forwardWhich of the following sets of vectors are linearly independent? (Check the boxes for linearly independent sets.) ☐ A. { 7 4 3 13 -9 8 -17 7 ☐ B. 0 -8 3 ☐ C. 0 ☐ D. -5 ☐ E. 3 ☐ F. 4 THarrow_forward3 and = 5 3 ---8--8--8 Let = 3 U2 = 1 Select all of the vectors that are in the span of {u₁, u2, u3}. (Check every statement that is correct.) 3 ☐ A. The vector 3 is in the span. -1 3 ☐ B. The vector -5 75°1 is in the span. ГОЛ ☐ C. The vector 0 is in the span. 3 -4 is in the span. OD. The vector 0 3 ☐ E. All vectors in R³ are in the span. 3 F. The vector 9 -4 5 3 is in the span. 0 ☐ G. We cannot tell which vectors are i the span.arrow_forward
- (20 p) 1. Find a particular solution satisfying the given initial conditions for the third-order homogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y(3)+2y"-y-2y = 0; y(0) = 1, y'(0) = 2, y"(0) = 0; y₁ = e*, y2 = e¯x, y3 = e−2x (20 p) 2. Find a particular solution satisfying the given initial conditions for the second-order nonhomogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y"-2y-3y = 6; y(0) = 3, y'(0) = 11 yc = c₁ex + c2e³x; yp = −2 (60 p) 3. Find the general, and if possible, particular solutions of the linear systems of differential equations given below using the eigenvalue-eigenvector method. (See Section 7.3 in your textbook if you need a review of the subject.) = a) x 4x1 + x2, x2 = 6x1-x2 b) x=6x17x2, x2 = x1-2x2 c) x = 9x1+5x2, x2 = −6x1-2x2; x1(0) = 1, x2(0)=0arrow_forwardFind the perimeter and areaarrow_forwardAssume {u1, U2, us} spans R³. Select the best statement. A. {U1, U2, us, u4} spans R³ unless u is the zero vector. B. {U1, U2, us, u4} always spans R³. C. {U1, U2, us, u4} spans R³ unless u is a scalar multiple of another vector in the set. D. We do not have sufficient information to determine if {u₁, u2, 43, 114} spans R³. OE. {U1, U2, 3, 4} never spans R³. F. none of the abovearrow_forward
- Assume {u1, U2, 13, 14} spans R³. Select the best statement. A. {U1, U2, u3} never spans R³ since it is a proper subset of a spanning set. B. {U1, U2, u3} spans R³ unless one of the vectors is the zero vector. C. {u1, U2, us} spans R³ unless one of the vectors is a scalar multiple of another vector in the set. D. {U1, U2, us} always spans R³. E. {U1, U2, u3} may, but does not have to, span R³. F. none of the abovearrow_forwardLet H = span {u, v}. For each of the following sets of vectors determine whether H is a line or a plane. Select an Answer u = 3 1. -10 8-8 -2 ,v= 5 Select an Answer -2 u = 3 4 2. + 9 ,v= 6arrow_forwardSolve for the matrix X: X (2 7³) x + ( 2 ) - (112) 6 14 8arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Sampling Methods and Bias with Surveys: Crash Course Statistics #10; Author: CrashCourse;https://www.youtube.com/watch?v=Rf-fIpB4D50;License: Standard YouTube License, CC-BY
Statistics: Sampling Methods; Author: Mathispower4u;https://www.youtube.com/watch?v=s6ApdTvgvOs;License: Standard YouTube License, CC-BY