Concept explainers
Videos
a.
To calculate: The probability that the outcome will be between $16,800 and $31,200.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
a.
Answer to Problem 20P
The probability that the outcome will be between $16,800 and $31,200 is 0.8664.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being equal to or greater than $16,800 is shown below.
The calculation of the expected value (Z) for the outcome being equal to or lower than $31,200 is shown below.
The Z values are positive as well as negative 1.5. Hence, the probability of the outcome being between $16,800 and $31,200 is 0.8664.
b.
To calculate: The probability that the outcome will be between $14,400 and $33,600.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
b.
Answer to Problem 20P
The probability that the outcome will be between $14,400 and $33,600 is 0.9544.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being equal to or greater than $14,400 is shown below.
The calculation of the expected value (Z) for the outcome being equal to or lower than $33,600 is shown below.
The Z values are positive as well as negative 2. Hence, the probability of the outcome being between $14,400 and $33,600 is 0.9544.
c.
To calculate: The probability that the outcome will be at least $14,400.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
c.
Answer to Problem 20P
The probability that the outcome will be at least $14,400 is 0.9544.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being at least $14,400 is shown below.
The expected value is 0.4772 when Z is (+ or -) 2 and 0.5000 when Z is 0. So, the probability of the outcome being at least $14,400 is 0.9772. The graph of this probability is shown below.
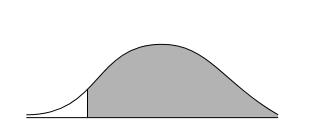
d.
To calculate: The probability that the outcome will be less than $31,900.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
d.
Answer to Problem 20P
The probability that the outcome will be less than $31,900 is 0.9544.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being at least $14,400 is shown below.
The expected value is 0.4505 when Z is (+ or -) 1.65 and 0.5000 when Z is 0. So, the probability of the outcome being at least $14,400 is 0.9505. The graph of this probability is shown below.
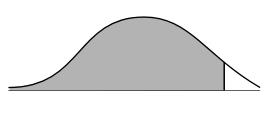
e.
To calculate: The probability that the outcome will be less than $19,200 or greater than $26,400.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
e.
Answer to Problem 20P
The probability that the outcome will be less than $19,200 or greater than $26,400 is 0.4672.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being less than $19,200 is shown below.
The expected value is 0.3413 when Z is (+ or -) 1 and 0.5000 when Z is 0. So, the probability of the outcome being less than $19,200 is 0.1587 (0.5000 – 0.3413).
The calculation of the expected value (Z) for the outcome being greater than $26,400 is shown below.
The expected value is 0.1915 when Z is (+ or -) 1 and 0.5000 when Z is 0. So, the probability of the outcome being at least $14,400 is 0.3085 (0.5000 – 0.1915).
Hence, the probability that the outcome will be less than $19,200 or greater than $26,400 is 0.4672. The graph of this probability is shown below.
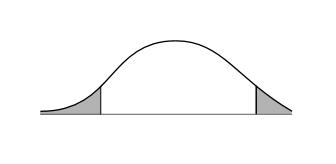
Want to see more full solutions like this?
Chapter 13 Solutions
EBK FOUNDATIONS OF FINANCIAL MANAGEMENT
- Dynamic Energy Wares (DEW) has decided to change the manner in which it distributes its products to large companies. The change in the distribution system comes at a time when DEW’s profits are declining. The declining profits might not be the sole reason for the change, but it appears to be the primary impetus for the decision. It also appears that the new policy requiring DEW’s distributors to increase inventory levels before the end of the fiscal year will artificially inflate DEW’s sales for the current year. However, DEW’s new policy does not require the distributors to pay for any increased inventory until next year (six months), and any unsold inventory can be returned after nine months. So, if the demand for DEW’s products actually is decreasing, the impact will appear on next year’s financial statements. If the financial manager actually intends to artificially inflate DEW’s profits this year, she must realize that such actions eventually will “catch up” with her. Discussion…arrow_forwardwhat is distributors’ meeting?arrow_forwardWhat is ethical dilemma?arrow_forward
- $1.35 Million for the below question is incorrect, Machine A is $1.81 and Machine B is $0.46 Million. The Perez Company has the opportunity to invest in one of two mutually exclusive machines that will produce a product it will need for the foreseeable future. Machine A costs $8 million but realizes after-tax inflows of $4.5 million per year for 4 years. After 4 years, the machine must be replaced. Machine B costs $17 million and realizes after-tax inflows of $4 million per year for 8 years, after which it must be replaced. Assume that machine prices are not expected to rise because inflation will be offset by cheaper components used in the machines. The cost of capital is 13%. Using the replacement chain approach to project analysis, by how much would the value of the company increase if it accepted the better machine? Round your answer to two decimal places. 1.) $1.35 millionarrow_forwardBuggies-Are-Us Steady Freddie, Inc Gang Buster Group g = 0 g = 55% Year 1 $3.51 (i.e., dividends are expected to remain at $3.053.05/share) (for the foreseeable future) Year 2 $4.04 Year 3 $4.63 Year 4 $5.36 Year 5 $6.15 Year 6 and beyond: g = 55%arrow_forwardProject S has a cost of $10,000 and is expected to produce benefits (cash flows) of $3,000 per year for 5 years. Project L costs $25,000 and is expected to produce cash flows of $7,400 per year for 5 years. Calculate the two projects' NPVs, assuming a cost of capital of 12%. Do not round intermediate calculations. Round your answers to the nearest cent. Calculate the two projects' PIs, assuming a cost of capital of 12%. Do not round intermediate calculations. Round your answers to three decimal places. Project L is not 1.07arrow_forward
- Wilbur and Orville are brothers. They're both serious investors, but they have different approaches to valuing stocks. Wilbur, the older brother, likes to use the dividend valuation model. Orville prefers the free cash flow to equity valuation model. As it turns out, right now, both of them are looking at the same stock-Wright First Aerodynmaics, Inc. (WFA). The company has been listed on the NYSE for over 50 years and is widely regarded as a mature, rock-solid, dividend-paying stock. The brothers have gathered the following information about WFA's stock: Current dividend (D) = $2.30/share Current free cash flow (FCF) = $1.5 million Expected growth rate of dividends and cash flows (g) = 5% Required rate of return (r) = 14% Shares outstanding 500,000 shares How would Wilbur and Orville each value this stock?arrow_forwardCompany P/S Multiples Facebook 13.33 Snap 18.22 Twitter 13.27arrow_forwardThe Perez Company has the opportunity to invest in one of two mutually exclusive machines that will produce a product it will need for the foreseeable future. Machine A costs $8 million but realizes after-tax inflows of $4.5 million per year for 4 years. After 4 years, the machine must be replaced. Machine B costs $17 million and realizes after-tax inflows of $4 million per year for 8 years, after which it must be replaced. Assume that machine prices are not expected to rise because inflation will be offset by cheaper components used in the machines. The cost of capital is 13%. Using the replacement chain approach to project analysis, by how much would the value of the company increase if it accepted the better machine? Round your answer to two decimal places. 1.) $ millionarrow_forward
- Wilbur and Orville are brothers. They're both serious investors, but they have different approaches to valuing stocks. Wilbur, the older brother, likes to use the dividend valuation model. Orville prefers the free cash flow to equity valuation model. As it turns out, right now, both of them are looking at the same stock-Wright First Aerodynmaics, Inc. (WFA). The company has been listed on the NYSE for over 50 years and is widely regarded as a mature, rock-solid, dividend-paying stock. The brothers have gathered the following information about WFA's stock: Current dividend (D) = $3.30/share Current free cash flow (FCF) = $1.5 million Expected growth rate of dividends and cash flows (g)=8% Required rate of return (r) = 13% Shares outstanding 500,000 shares How would Wilbur and Orville each value this stock? The stock price from Wilbur's valuation is $ (Round to the nearest cent.)arrow_forwardThe Perez Company has the opportunity to invest in one of two mutually exclusive machines that will produce a product it will need for the foreseeable future. Machine A costs $8 million but realizes after-tax inflows of $4.5 million per year for 4 years. After 4 years, the machine must be replaced. Machine B costs $17 million and realizes after-tax inflows of $4 million per year for 8 years, after which it must be replaced. Assume that machine prices are not expected to rise because inflation will be offset by cheaper components used in the machines. The cost of capital is 13%. Using the replacement chain approach to project analysis, by how much would the value of the company increase if it accepted the better machine? Round your answer to two decimal places. 1.) $ million What is the equivalent annual annuity for each machine? Do not round intermediate calculations. Round your answers to two decimal places. 2.) Machine A: $ million 3.) Machine B: $ millionarrow_forwardYou expect to have $29,865. You plan to make X savings contribution of $1,690 per month. The expected return is 0.92 percent per month and the first regular savings contribution will be made later today. What is X? Round to 2 decimal places.arrow_forward
Essentials of Business Analytics (MindTap Course ...StatisticsISBN:9781305627734Author:Jeffrey D. Camm, James J. Cochran, Michael J. Fry, Jeffrey W. Ohlmann, David R. AndersonPublisher:Cengage Learning
EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT