
Each edge of a cubical box has length 1 m. The box contains nine spherical balls with the same radius r. The center of one ball is at the center of the cube and it touches the other eight balls. Each of the other eight balls touches three sides of the box. Thus the balls are tightly packed in the box (see the figure). Find r. (If you have trouble with this problem, read about the problem-solving strategy entitled Use Analogy on page 98.)
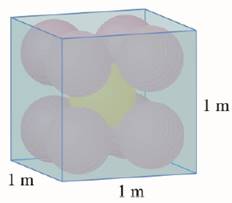
To find:
The radius
Answer to Problem 1P
Solution:
The radius of each ball is
Explanation of Solution
1) Concept:
We create an analogous problem in two dimensions and use the strategy in two dimension to solve the problem in three dimension.
2) Calculation:
Since three dimensional situations are often diffucult to visualize and work with, we create an analogous problem in two dimensions and use the strategy in two dimension to solve the problem in three dimension.
Let us try to find the analogous problem in two dimensions. The analogue of a cube is a square, and the analogue of a sphere is a circle.Thus, a simillar problem in two dimensions is as follows:
What is r, if five circles with the same radius r are contained in a square of side 1m so that the circles touch each other and four of the circles touch two sides of square, as shown in the figure,
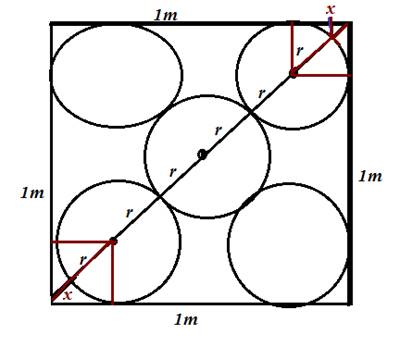
By pythagorean Theorem, the diagonal of the square is
Also from the figure, the diagonal of the square is
Therefore,
But,
Therefore,
Therefore,
That is,
Therefore,
Let’s use this idea to solve the original three dimensional problem.
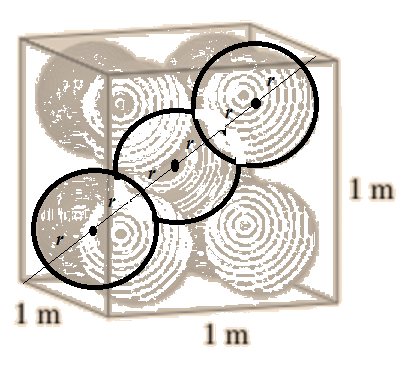
The diagonal of the cube is
And the diagonal of the cube is also
Therefore,
where
Therefore,
Therefore,
That is,
Therefore,
By rationalization,
Therefore, the radius of each ball is
Conclusion:
The radius of each ball is
Want to see more full solutions like this?
Chapter 12 Solutions
Calculus (MindTap Course List)
- I need help in ensuring that I explain it propleryy in the simplifest way as possiblearrow_forwardI need help making sure that I explain this part accutartly.arrow_forwardPlease help me with this question as I want to know how can I perform the partial fraction decompostion on this alebgric equation to find the time-domain of y(t)arrow_forward
- Please help me with this question as I want to know how can I perform the partial fraction on this alebgric equation to find the time-domain of y(t)arrow_forwardEvaluate F³ - dr where ♬ = (4z, -4y, x), and C' is given by (t) = (sin(t), t, cos(t)), 0≤t≤ñ .arrow_forwardMid-Term Review Find the formula for (f + g)(x). f(x) = x² - 10x + 25 and g(x) = x² - 10x + 24 (f + g) (x) = [ 2 ]x² X + DELL Skip Sarrow_forward
- Calculus III May I please have some elaborations on Example 2 part a? Thank you.arrow_forward1. A bicyclist is riding their bike along the Chicago Lakefront Trail. The velocity (in feet per second) of the bicyclist is recorded below. Use (a) Simpson's Rule, and (b) the Trapezoidal Rule to estimate the total distance the bicyclist traveled during the 8-second period. t 0 2 4 6 8 V 10 15 12 10 16 2. Find the midpoint rule approximation for (a) n = 4 +5 x²dx using n subintervals. 1° 2 (b) n = 8 36 32 28 36 32 28 24 24 20 20 16 16 12 8- 4 1 2 3 4 5 6 12 8 4 1 2 3 4 5 6arrow_forward= 5 37 A 4 8 0.5 06 9arrow_forward

 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill





