
The data summarized in the accompanying table are from the paper “Gender Differences in Food Selections of Students at a Historically Black College and University” (College Student Journal [2009]: 800–806). Suppose that the data resulted from classifying each person in a random sample of 48 male students and each person in a random sample of 91 female students at a particular college according to their response to a question about whether they usually eat three meals a day or rarely eat three meals a day.

- a. Is there evidence that the proportions falling into each of the two response categories are not the same for males and females? Use the X2 statistic to test the relevant hypotheses with a significance level of 0.05.
- b. Are the calculations and conclusions from Part (a) consistent with the accompanying Minitab output?
Expected counts are printed below observed counts
Chi-Square contributions are printed below expected counts
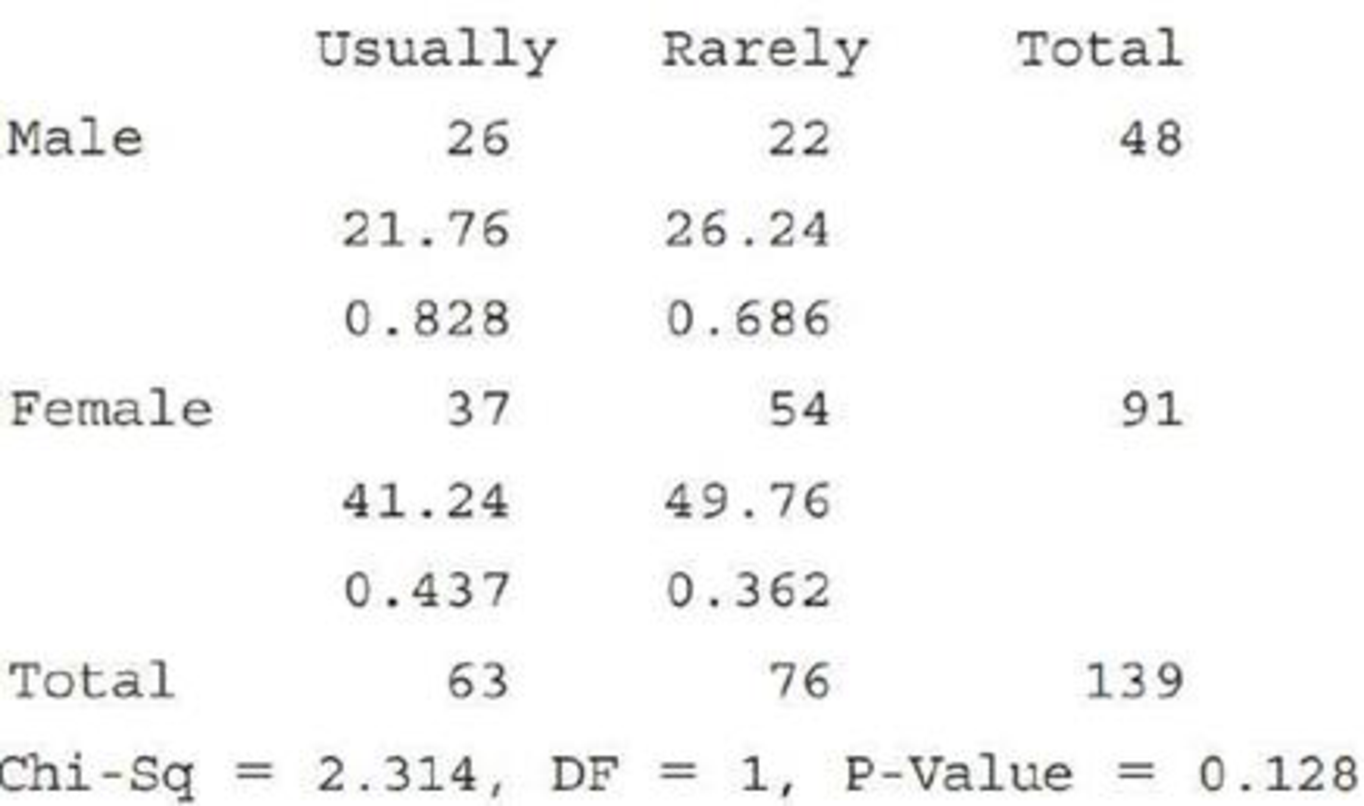
- c. Because the response variable in this exercise has only two categories (usually and rarely), we could have also answered the question posed in Part (a) by carrying out a two-sample z test of H0: p1 − p2 = 0 versus Ha: p1 − p2 ≠ 0, where p1 is the proportion who usually eat three meals a day for males and p2 is the proportion who usually eat three meals a day for females. Minitab output from the two-sample z test is shown below. Using a significance level of 0.05, does the two-sample z test lead to the same conclusion as in Part (a)?
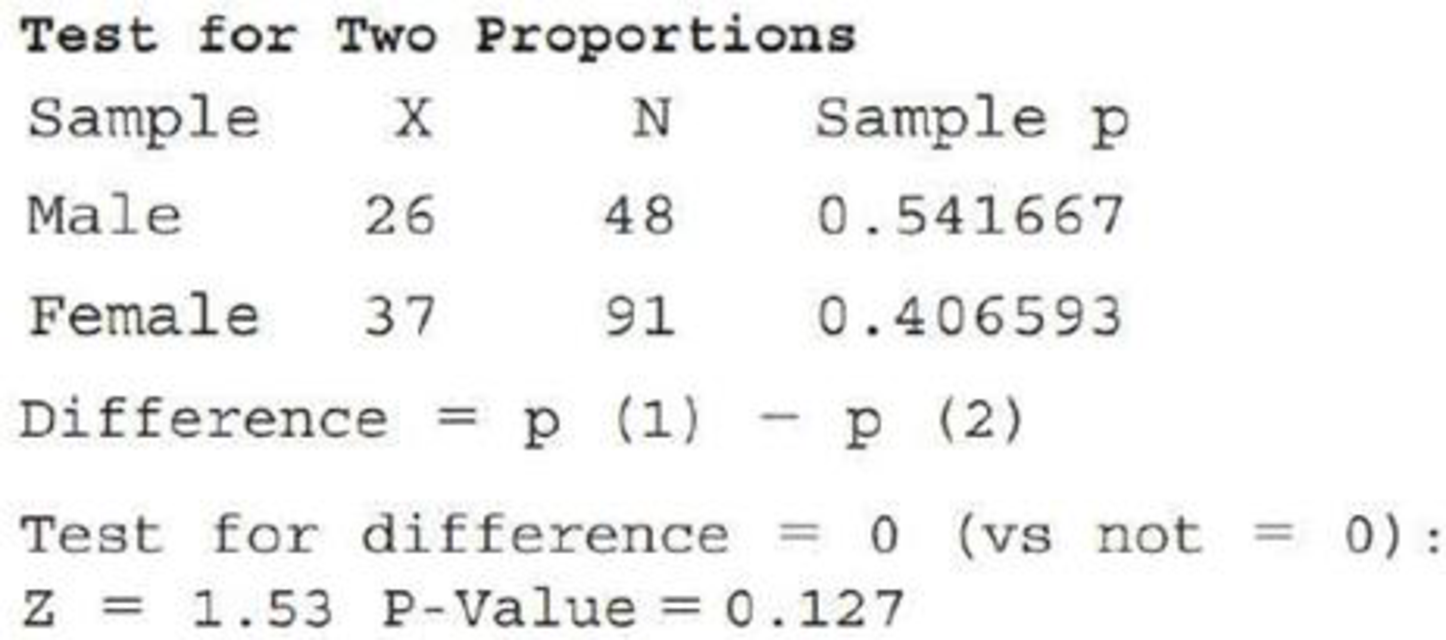
- d. How do the P-values from the tests in Parts (a) and (c) compare? Is this surprising? Explain.
a.
Test whether the proportions falling into each of the two response categories for males and females are same or not.
Answer to Problem 25E
There is no convincing evidence that the proportions falling into each of the two response categories for males and females are not same.
Explanation of Solution
Given table represents classification of male and female students according to their response about whether they usually eat three meals a day or rarely eat three meals a day.
In order to test the proportions falling into each of the two response categories for males and females are same or not, the appropriate test is
The steps in chi-square test for homogeneity is as follows.
Null and alternative Hypotheses:
Null hypothesis:
Alternative hypothesis:
Level of significance:
Assumptions:
- It is given that data resulted from classifying each person in a random sample of male and female students at a particular college.
- The expected cell counts are calculated as shown below.
| Usually eat 3 meals a day | Rarely eat 3 meals a day | Total | |
| Male | 48 | ||
| Female | 91 | ||
| Total | 63 | 76 | 139 |
From the expected cell counts table, it is observed that all the expected counts are greater than 5.
Test Statistic:
Chi-square statistic:
Degrees of freedom:
Here, number of rows is 2 and the number of columns is 2. The degrees of freedom is calculated as follows.
From the calculations,
P-value:
From Table 8-Upper-Tail Areas for Chi-Square Distributions, the Right-tail area is greater than 0.100 for the chi-squared values that are less than 2.70.
Thus, P-value > 0.100.
Decision rule:
- If P-value is less than or equal to the level of significance, reject the null hypothesis.
- Otherwise fail to reject the null hypothesis.
Conclusion:
Here the level of significance is 0.05.
Here, P-value is greater than the level of significance.
That is,
Therefore, fail to reject the null hypothesis. Therefore, there is no convincing evidence that the proportions falling into each of the two response categories for males and females are not same.
b.
Check whether the calculations and conclusions from Part (a) consistent with the accompanying Minitab output.
Explanation of Solution
From Part (a), the chi-square value obtained is
In the given MINITAB output, chi-square value is 2.314 and P-value is 0.128.
Since,
Hence, the calculations and conclusions from Part (a) consistent with the accompanying Minitab output.
c.
Check whether the two-sample z test lead to the same conclusion as in Part (a).
Answer to Problem 25E
The two-sample z test lead to the same conclusion as in Part (a).
Explanation of Solution
From the given output for test for two proportions,
Conclusion:
Here the level of significance is 0.05.
Here, P-value is greater than the level of significance.
That is,
Therefore, fail to reject the null hypothesis. Therefore, there is no convincing evidence that the proportions falling in the two response categories are not same for males and females.
Thus, the two-sample z test lead to the same conclusion as in Part (a).
d.
Explain the comparison of P-values from the tests in Parts (a) and (c).
Explanation of Solution
The P-value obtained in Part (a) is greater than 0.100. And, the P-value obtained in Part (c) is 0.127.
There is some difference in P-value. But both are greater than 0.100.
This is not surprising as both chi-square statistic and z-statistic measure the probability of getting sample proportions that are far from the expected proportions under null hypothesis.
Want to see more full solutions like this?
Chapter 12 Solutions
INTRODUCTION TO STATISTICS & DATA ANALYS
- 5. Probability Distributions – Continuous Random Variables A factory machine produces metal rods whose lengths (in cm) follow a continuous uniform distribution on the interval [98, 102]. Questions: a) Define the probability density function (PDF) of the rod length.b) Calculate the probability that a randomly selected rod is shorter than 99 cm.c) Determine the expected value and variance of rod lengths.d) If a sample of 25 rods is selected, what is the probability that their average length is between 99.5 cm and 100.5 cm? Justify your answer using the appropriate distribution.arrow_forward2. Hypothesis Testing - Two Sample Means A nutritionist is investigating the effect of two different diet programs, A and B, on weight loss. Two independent samples of adults were randomly assigned to each diet for 12 weeks. The weight losses (in kg) are normally distributed. Sample A: n = 35, 4.8, s = 1.2 Sample B: n=40, 4.3, 8 = 1.0 Questions: a) State the null and alternative hypotheses to test whether there is a significant difference in mean weight loss between the two diet programs. b) Perform a hypothesis test at the 5% significance level and interpret the result. c) Compute a 95% confidence interval for the difference in means and interpret it. d) Discuss assumptions of this test and explain how violations of these assumptions could impact the results.arrow_forward1. Sampling Distribution and the Central Limit Theorem A company produces batteries with a mean lifetime of 300 hours and a standard deviation of 50 hours. The lifetimes are not normally distributed—they are right-skewed due to some batteries lasting unusually long. Suppose a quality control analyst selects a random sample of 64 batteries from a large production batch. Questions: a) Explain whether the distribution of sample means will be approximately normal. Justify your answer using the Central Limit Theorem. b) Compute the mean and standard deviation of the sampling distribution of the sample mean. c) What is the probability that the sample mean lifetime of the 64 batteries exceeds 310 hours? d) Discuss how the sample size affects the shape and variability of the sampling distribution.arrow_forward
- A biologist is investigating the effect of potential plant hormones by treating 20 stem segments. At the end of the observation period he computes the following length averages: Compound X = 1.18 Compound Y = 1.17 Based on these mean values he concludes that there are no treatment differences. 1) Are you satisfied with his conclusion? Why or why not? 2) If he asked you for help in analyzing these data, what statistical method would you suggest that he use to come to a meaningful conclusion about his data and why? 3) Are there any other questions you would ask him regarding his experiment, data collection, and analysis methods?arrow_forwardBusinessarrow_forwardWhat is the solution and answer to question?arrow_forward
- To: [Boss's Name] From: Nathaniel D Sain Date: 4/5/2025 Subject: Decision Analysis for Business Scenario Introduction to the Business Scenario Our delivery services business has been experiencing steady growth, leading to an increased demand for faster and more efficient deliveries. To meet this demand, we must decide on the best strategy to expand our fleet. The three possible alternatives under consideration are purchasing new delivery vehicles, leasing vehicles, or partnering with third-party drivers. The decision must account for various external factors, including fuel price fluctuations, demand stability, and competition growth, which we categorize as the states of nature. Each alternative presents unique advantages and challenges, and our goal is to select the most viable option using a structured decision-making approach. Alternatives and States of Nature The three alternatives for fleet expansion were chosen based on their cost implications, operational efficiency, and…arrow_forwardBusinessarrow_forwardWhy researchers are interested in describing measures of the center and measures of variation of a data set?arrow_forward
- WHAT IS THE SOLUTION?arrow_forwardThe following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8arrow_forwardII Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL



