Bundle: Calculus: Early Transcendental Functions, Loose-leaf Version, 6th + WebAssign Printed Access Card for Larson/Edwards' Calculus: Early Transcendental Functions, 6th Edition, Multi-Term
Bundle: Calculus: Early Transcendental Functions, Loose-leaf Version, 6th + WebAssign Printed Access Card for Larson/Edwards' Calculus: Early Transcendental Functions, 6th Edition, Multi-Term
6th Edition
ISBN: 9781305714045
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
bartleby

Videos

Textbook Question
Book Icon
Chapter 12.1, Problem 82E

HOW DO YOU SEE IT? The four figures below are graphs of the vector-valued function r ( t ) = 4 cos t i + 4 sin t j + t 4 k .

Match each of the four graphs with the point in space from which the helix is viewed.

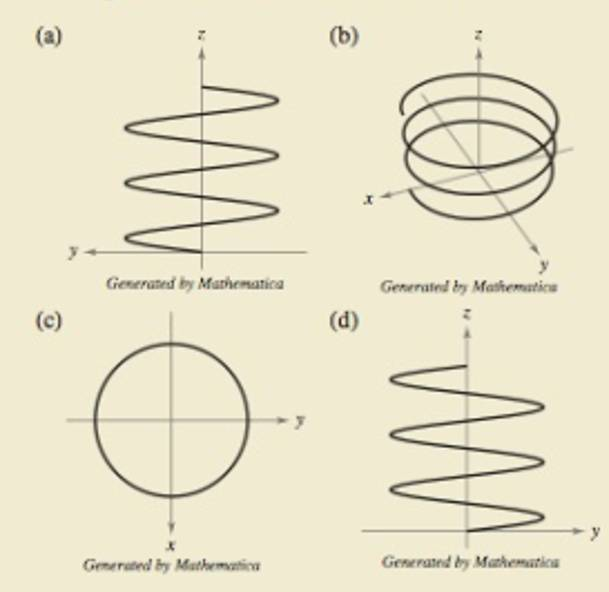
Chapter 12.1, Problem 82E, HOW DO YOU SEE IT? The four figures below are graphs of the vector-valued function

(i) (0, 0, 20)

(ii) (20, 0, 0)

(iii) ( − 20, 0, 0 )

(iv) (10, 20, 10)

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 12.1, Problem 81E
Next
Chapter 12.1, Problem 83E
Students have asked these similar questions
Explain the focus and reasons for establishment of 12.4.1(root test) and 12.4.2(ratio test)
use Integration by Parts to derive 12.6.1
Explain the relationship between 12.3.6, (case A of 12.3.6) and 12.3.7

Chapter 12 Solutions

Bundle: Calculus: Early Transcendental Functions, Loose-leaf Version, 6th + WebAssign Printed Access Card for Larson/Edwards' Calculus: Early Transcendental Functions, 6th Edition, Multi-Term

Ch. 12.1 - Finding the domain In exercises 3-10 find the...Ch. 12.1 - Prob. 2ECh. 12.1 - Finding the domain In exercises 3-10 find the...Ch. 12.1 - Finding the domain In exercises 3-10 find the...Ch. 12.1 - Finding the Domain In Exercises 3-10, find the...Ch. 12.1 - Finding the Domain In Exercises 3-10, find the...Ch. 12.1 - Prob. 7ECh. 12.1 - Finding the domain In exercises 3-10 find the...Ch. 12.1 - Evaluating a function In Exercises 11 and 12...Ch. 12.1 - Evaluating a function In Exercises 11 and 12...
Ch. 12.1 - Evaluating a Function In Exercises 912. evaluate...Ch. 12.1 - Evaluating a FunctionIn Exercises 912. evaluate...Ch. 12.1 - Prob. 13ECh. 12.1 - Writing a Vector-Valued Function In Exercises...Ch. 12.1 - Prob. 15ECh. 12.1 - Prob. 16ECh. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - Matching In Exercises 19-22. match the equation...Ch. 12.1 - Prob. 20ECh. 12.1 - Prob. 21ECh. 12.1 - Matching In Exercises 19-22, match the equation...Ch. 12.1 - Prob. 23ECh. 12.1 - Prob. 24ECh. 12.1 - Prob. 25ECh. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - Prob. 29ECh. 12.1 - Prob. 30ECh. 12.1 - Prob. 31ECh. 12.1 - Prob. 32ECh. 12.1 - Prob. 33ECh. 12.1 - Prob. 34ECh. 12.1 - Prob. 35ECh. 12.1 - Prob. 36ECh. 12.1 - Prob. 37ECh. 12.1 - Prob. 38ECh. 12.1 - Prob. 39ECh. 12.1 - Prob. 42ECh. 12.1 - Identifying a Common Curve In Exercises 3942, use...Ch. 12.1 - Prob. 41ECh. 12.1 - Transformation of a vector valued valued in...Ch. 12.1 - Transformations of Vector-Valued Functions In...Ch. 12.1 - Prob. 45ECh. 12.1 - Prob. 46ECh. 12.1 - Prob. 47ECh. 12.1 - Prob. 48ECh. 12.1 - Prob. 49ECh. 12.1 - Prob. 50ECh. 12.1 - Prob. 51ECh. 12.1 - Prob. 52ECh. 12.1 - Prob. 53ECh. 12.1 - Prob. 54ECh. 12.1 - Prob. 55ECh. 12.1 - Prob. 56ECh. 12.1 - Prob. 57ECh. 12.1 - Prob. 58ECh. 12.1 - Prob. 59ECh. 12.1 - Prob. 60ECh. 12.1 - Prob. 61ECh. 12.1 - Prob. 62ECh. 12.1 - Finding a Limit In Exercises 65-70, find the limit...Ch. 12.1 - Prob. 64ECh. 12.1 - Prob. 65ECh. 12.1 - Prob. 66ECh. 12.1 - Finding a Limit In Exercises 65-70, find the limit...Ch. 12.1 - Prob. 68ECh. 12.1 - Prob. 69ECh. 12.1 - Prob. 70ECh. 12.1 - Prob. 71ECh. 12.1 - Prob. 72ECh. 12.1 - Prob. 73ECh. 12.1 - Prob. 74ECh. 12.1 - Prob. 75ECh. 12.1 - Prob. 76ECh. 12.1 - Prob. 77ECh. 12.1 - Prob. 78ECh. 12.1 - Continuity of a Vector-Valued Function State the...Ch. 12.1 - Prob. 80ECh. 12.1 - Prob. 81ECh. 12.1 - HOW DO YOU SEE IT? The four figures below are...Ch. 12.1 - Proof Let r(t) and u(t) be vector-valued functions...Ch. 12.1 - Proof Let r(t) and u(t) be vector-valued functions...Ch. 12.1 - Proof Prove that if r is a vector-valued function...Ch. 12.1 - Prob. 86ECh. 12.1 - Prob. 89ECh. 12.1 - Prob. 90ECh. 12.1 - Prob. 87ECh. 12.1 - Prob. 88ECh. 12.1 - Prob. 91ECh. 12.1 - Prob. 92ECh. 12.1 - Prob. 93ECh. 12.1 - Prob. 94ECh. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - Prob. 7ECh. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Prob. 18ECh. 12.2 - Prob. 19ECh. 12.2 - Prob. 20ECh. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Prob. 23ECh. 12.2 - Prob. 24ECh. 12.2 - Prob. 25ECh. 12.2 - Prob. 26ECh. 12.2 - Prob. 27ECh. 12.2 - Prob. 28ECh. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Finding Intervals on Which a Curve Is Smooth In...Ch. 12.2 - Prob. 35ECh. 12.2 - Prob. 36ECh. 12.2 - Prob. 37ECh. 12.2 - Prob. 38ECh. 12.2 - Prob. 39ECh. 12.2 - Prob. 40ECh. 12.2 - Using Two Methods In Exercises 37 and 38, Find (a)...Ch. 12.2 - Prob. 42ECh. 12.2 - Prob. 43ECh. 12.2 - Prob. 44ECh. 12.2 - Finding an Indefinite Integral In Exercises 39-46,...Ch. 12.2 - Prob. 46ECh. 12.2 - Prob. 47ECh. 12.2 - Prob. 48ECh. 12.2 - Prob. 49ECh. 12.2 - Finding an Indefinite Integral In Exercises 4350,...Ch. 12.2 - Prob. 51ECh. 12.2 - Prob. 52ECh. 12.2 - Prob. 53ECh. 12.2 - Prob. 54ECh. 12.2 - Prob. 55ECh. 12.2 - Prob. 56ECh. 12.2 - Finding an Antiderivative In Exercises 53-58, find...Ch. 12.2 - Prob. 58ECh. 12.2 - Prob. 59ECh. 12.2 - Prob. 60ECh. 12.2 - Finding an Antiderivative In Exercises 53-58, find...Ch. 12.2 - Prob. 62ECh. 12.2 - Prob. 63ECh. 12.2 - Prob. 64ECh. 12.2 - Prob. 65ECh. 12.2 - Prob. 66ECh. 12.2 - Prob. 67ECh. 12.2 - Prob. 68ECh. 12.2 - Prob. 69ECh. 12.2 - Prob. 70ECh. 12.2 - Prob. 71ECh. 12.2 - Prob. 72ECh. 12.2 - Prob. 73ECh. 12.2 - Prob. 74ECh. 12.2 - Particle Motion A particle moves in the xy-plane...Ch. 12.2 - Prob. 76ECh. 12.2 - Prob. 77ECh. 12.2 - Prob. 78ECh. 12.2 - Prob. 79ECh. 12.2 - Prob. 80ECh. 12.2 - Prob. 81ECh. 12.2 - Prob. 82ECh. 12.3 - Prob. 1ECh. 12.3 - Prob. 2ECh. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 - Prob. 8ECh. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.3 - Prob. 19ECh. 12.3 - Prob. 20ECh. 12.3 - Prob. 21ECh. 12.3 - Prob. 22ECh. 12.3 - Finding a Position Vector by Integration In...Ch. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Prob. 30ECh. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Projectile Motion In Exercises 27-40, use the...Ch. 12.3 - A bomber is flying horizontally at an altitude of...Ch. 12.3 - Prob. 35ECh. 12.3 - Prob. 36ECh. 12.3 - Prob. 37ECh. 12.3 - Prob. 38ECh. 12.3 - Prob. 39ECh. 12.3 - Prob. 40ECh. 12.3 - Shot-Put Throw The path of a shot thrown at an...Ch. 12.3 - Prob. 42ECh. 12.3 - Prob. 43ECh. 12.3 - Prob. 44ECh. 12.3 - Prob. 45ECh. 12.3 - Prob. 46ECh. 12.3 - Prob. 47ECh. 12.3 - Prob. 48ECh. 12.3 - Circular Motion In Exercises 49 and 50, use the...Ch. 12.3 - Circular Motion In Exercises 51 and 52, use the...Ch. 12.3 - Prob. 51ECh. 12.3 - Prob. 52ECh. 12.3 - Proof Prove that when an object is traveling at a...Ch. 12.3 - Prob. 54ECh. 12.3 - Prob. 55ECh. 12.3 - Prob. 56ECh. 12.3 - Prob. 57ECh. 12.3 - HOW DO YOU SEE IT? The graph shows the path of a...Ch. 12.3 - Prob. 59ECh. 12.3 - Prob. 60ECh. 12.3 - Prob. 62ECh. 12.3 - Prob. 61ECh. 12.4 - Prob. 44ECh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - Prob. 5ECh. 12.4 - Prob. 6ECh. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - Finding the Principal Unit Normal Vector In...Ch. 12.4 - Finding the Principal Unit Normal Vector In...Ch. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Finding the Principal Unit Normal Vector In...Ch. 12.4 - Finding the Principal Unit Normal Vector In...Ch. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 35ECh. 12.4 - Finding Tangential and Normal Components of...Ch. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - Prob. 26ECh. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 37ECh. 12.4 - Prob. 38ECh. 12.4 - Prob. 39ECh. 12.4 - Prob. 40ECh. 12.4 - Finding Tangential and Normal Components of...Ch. 12.4 - Prob. 42ECh. 12.4 - Prob. 43ECh. 12.4 - Prob. 45ECh. 12.4 - Prob. 46ECh. 12.4 - Finding Vectors An object moves along the path...Ch. 12.4 - Prob. 48ECh. 12.4 - Prob. 49ECh. 12.4 - Prob. 50ECh. 12.4 - Prob. 51ECh. 12.4 - Prob. 52ECh. 12.4 - Prob. 53ECh. 12.4 - Prob. 54ECh. 12.4 - Prob. 55ECh. 12.4 - Prob. 56ECh. 12.4 - Prob. 57ECh. 12.4 - Prob. 58ECh. 12.4 - Prob. 59ECh. 12.4 - Prob. 60ECh. 12.4 - Projectile Motion Find the tangential and normal...Ch. 12.4 - Prob. 62ECh. 12.4 - Prob. 63ECh. 12.4 - Prob. 64ECh. 12.4 - Air Traffic Control Because of a storm, ground...Ch. 12.4 - Projectile Motion A plane flying at an altitude of...Ch. 12.4 - Prob. 67ECh. 12.4 - Prob. 68ECh. 12.4 - Prob. 69ECh. 12.4 - Prob. 70ECh. 12.4 - Prob. 71ECh. 12.4 - Prob. 72ECh. 12.4 - Prob. 73ECh. 12.4 - Prob. 74ECh. 12.4 - Prob. 75ECh. 12.4 - Prob. 76ECh. 12.4 - Proof Prove that the sector T(t) is 0 for an...Ch. 12.4 - Prob. 78ECh. 12.4 - Prob. 79ECh. 12.4 - Prob. 80ECh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - Prob. 5ECh. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Projectile MotionRepeat Exercise 7 for a baseball...Ch. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.5 - Investigation Consider the graph of the...Ch. 12.5 - InvestigationRepeat Exercise 15 for the...Ch. 12.5 - Prob. 17ECh. 12.5 - Prob. 18ECh. 12.5 - Prob. 19ECh. 12.5 - Prob. 20ECh. 12.5 - Prob. 21ECh. 12.5 - Prob. 22ECh. 12.5 - Prob. 23ECh. 12.5 - Prob. 24ECh. 12.5 - Prob. 25ECh. 12.5 - Prob. 26ECh. 12.5 - Prob. 27ECh. 12.5 - Prob. 28ECh. 12.5 - Prob. 29ECh. 12.5 - Prob. 30ECh. 12.5 - Prob. 31ECh. 12.5 - Prob. 32ECh. 12.5 - Finding Curvature In Exercises 29-36, find the...Ch. 12.5 - Prob. 34ECh. 12.5 - Prob. 35ECh. 12.5 - Prob. 36ECh. 12.5 - Prob. 37ECh. 12.5 - Prob. 38ECh. 12.5 - Prob. 39ECh. 12.5 - Finding Curvature In Exercises 37-40, find the...Ch. 12.5 - Prob. 41ECh. 12.5 - Prob. 42ECh. 12.5 - Prob. 43ECh. 12.5 - Prob. 44ECh. 12.5 - Prob. 45ECh. 12.5 - Prob. 46ECh. 12.5 - Prob. 47ECh. 12.5 - Prob. 48ECh. 12.5 - Prob. 49ECh. 12.5 - Maximum Curvature In Exercises 49-54, (a) find the...Ch. 12.5 - Prob. 51ECh. 12.5 - Prob. 52ECh. 12.5 - Maximum Curvature In Exercises 49-54, (a) find the...Ch. 12.5 - Prob. 54ECh. 12.5 - Prob. 55ECh. 12.5 - Prob. 56ECh. 12.5 - Prob. 57ECh. 12.5 - Prob. 58ECh. 12.5 - Prob. 59ECh. 12.5 - Prob. 60ECh. 12.5 - Prob. 61ECh. 12.5 - Prob. 62ECh. 12.5 - Prob. 63ECh. 12.5 - Prob. 64ECh. 12.5 - Prob. 65ECh. 12.5 - Prob. 66ECh. 12.5 - Prob. 67ECh. 12.5 - The smaller the curvature of a bend in a road, the...Ch. 12.5 - Prob. 69ECh. 12.5 - Prob. 70ECh. 12.5 - Prob. 71ECh. 12.5 - Prob. 72ECh. 12.5 - Prob. 73ECh. 12.5 - Prob. 74ECh. 12.5 - Prob. 75ECh. 12.5 - Prob. 76ECh. 12.5 - Prob. 77ECh. 12.5 - Prob. 78ECh. 12.5 - Prob. 79ECh. 12.5 - Prob. 80ECh. 12.5 - Prob. 81ECh. 12.5 - Prob. 82ECh. 12.5 - Prob. 83ECh. 12.5 - Prob. 84ECh. 12.5 - True or False? In Exercises 83-86, determine...Ch. 12.5 - Prob. 86ECh. 12.5 - Prob. 87ECh. 12.5 - Prob. 88ECh. 12.5 - Prob. 89ECh. 12.5 - Prob. 90ECh. 12.5 - Prob. 91ECh. 12.5 - Prob. 92ECh. 12.5 - Prob. 93ECh. 12.5 - Prob. 94ECh. 12.5 - Prob. 95ECh. 12.5 - Prob. 96ECh. 12 - Domain and Continuity In Exercises 1-4, (a) And...Ch. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - Evaluating a Function In Exercises 5 and 6....Ch. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Prob. 16RECh. 12 - Prob. 17RECh. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 26RECh. 12 - Prob. 25RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - Prob. 30RECh. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Prob. 36RECh. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 40RECh. 12 - Prob. 39RECh. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 44RECh. 12 - Prob. 45RECh. 12 - Prob. 46RECh. 12 - Prob. 47RECh. 12 - Prob. 48RECh. 12 - Prob. 49RECh. 12 - Prob. 50RECh. 12 - Prob. 51RECh. 12 - Prob. 52RECh. 12 - Prob. 53RECh. 12 - Prob. 54RECh. 12 - Prob. 55RECh. 12 - Prob. 56RECh. 12 - Prob. 57RECh. 12 - Prob. 58RECh. 12 - Prob. 59RECh. 12 - Prob. 60RECh. 12 - Prob. 61RECh. 12 - Prob. 62RECh. 12 - Prob. 63RECh. 12 - Finding Curvature In Exercises 63-66, find the...Ch. 12 - Prob. 65RECh. 12 - Prob. 66RECh. 12 - Prob. 67RECh. 12 - Finding Curvature in Rectangular Coordinates In...Ch. 12 - Finding Curvature in Rectangular Coordinates In...Ch. 12 - Prob. 70RECh. 12 - Prob. 71RECh. 12 - Cornu Spiral The cornu spiral is given by...Ch. 12 - Prob. 2PSCh. 12 - Prob. 3PSCh. 12 - Projectile Motion Repeat Exercise 3 for the case...Ch. 12 - Prob. 5PSCh. 12 - Cardioid Consider the cardioid r=1cos,02 as shown...Ch. 12 - Prob. 7PSCh. 12 - Prob. 8PSCh. 12 - Prob. 9PSCh. 12 - Prob. 10PSCh. 12 - Prob. 11PSCh. 12 - Exit Ramp A highway has an exit ramp that begins...Ch. 12 - Prob. 13PSCh. 12 - Ferris Wheel You want to toss an object to a...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
Basic Differentiation Rules For Derivatives; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=IvLpN1G1Ncg;License: Standard YouTube License, CC-BY