Trigonometry plus MyLab Math with Pearson eText -- Access Card Package (11th Edition)
Trigonometry plus MyLab Math with Pearson eText -- Access Card Package (11th Edition)
11th Edition
ISBN: 9780134307008
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.2, Problem 71E

Solar Eclipse on Mars (Refer to Exercise 69.) The sun’s distance from the surface of Mars is approximately 142,000,000 mi. One of Mars’ two moons, Phobos, has a maximum diameter of 17.4 mi. (Source: World Almanac and Book of Facts.)

Calculate the maximum distance, to the nearest hundred miles, that the moon Phobos can be from Mars for a total eclipse of the sun to occur on Mars.

Phobos is approximately 5800 mi from Mars. Is it possible for Phobos to cause a total eclipse on Mars?

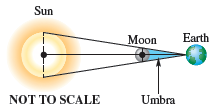
Solar Eclipse on Earth The sun has a diameter of about 865,000 mi with a maximum distance from Earth's surface of about 94,500,000 mi. The moon has a smaller diameter of 2159 mi. For a total solar eclipse to occur, the moon must pass between Earth and the sun. The moon must also be close enough to Earth for the moon’s umbra (shadow) to reach the surface of Earth. (Source: Karttunen, H., P. Kröger, H. Oja, M. Putannen, and K. Donners, Editors, Fundamental Astronomy, Fourth Edition, Springer-Verlag.)

Calculate the maximum distance, to the nearest thousand miles, that the moon can be from Earth and still have a total solar eclipse occur. (Hint: Use similar triangles.)

The closest approach of the moon to Earth’s surface was 225,745 mi and the farthest was 251,978 mi. (Source: World Almanac and Book of Facts.) Can a total solar eclipse occur every time the moon is between Earth and the sun?

Chapter 1.2, Problem 71E, Solar Eclipse on Mars (Refer to Exercise 69.) The suns distance from the surface of Mars is

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.2, Problem 70E
Next
Chapter 1.2, Problem 72E
Students have asked these similar questions
The hydraulic cylinder BC exerts on member AB a force P directed along line BC. The force P must have a 560-N component perpendicular to member AB. A M 45° 30° Determine the magnitude of the force P. The magnitude of the force P is N. 8
need help with my homework
Two planes are flying at the same altitude. One airplane is 60 miles due north of the control tower.Another airplane is located 70 miles from the tower at a heading of 80° east of south. To thenearest tenth of a mile, how far apart are the two airplanes?

Chapter 1 Solutions

Trigonometry plus MyLab Math with Pearson eText -- Access Card Package (11th Edition)

Ch. 1.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 1.1 - If the measure of an angle is x, its supplement...Ch. 1.1 - 3. If the measure of an angle is x°, its...Ch. 1.1 - 4. The measure of an angle that is its own...Ch. 1.1 - The measure of an angle that is its own supplement...Ch. 1.1 - One minute, written 1, is_________ of a degree.Ch. 1.1 - 7. One second, written 1″, is ______ of a...Ch. 1.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 1.1 - 55.25 written in degrees and minutes is ________.Ch. 1.1 - 10. If n represents any integer, then an...
Ch. 1.1 - Find the measure of (a) the complement and (b)...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of (a) the complement and (b)...Ch. 1.1 - Find the measure of (a) the complement and (b)...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of (a) the complement and (b)...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of (a) the complement and (b)...Ch. 1.1 - Find the measure of (a) the complement and (b) the...Ch. 1.1 - Find the measure of each marked angle. See...Ch. 1.1 - Find the measure of each marked angle. See...Ch. 1.1 - Find the measure of each marked angle. See...Ch. 1.1 - Find the measure of each marked angle. See...Ch. 1.1 - Find the measure of each marked angle. See...Ch. 1.1 - Find the measure of each marked angle. See...Ch. 1.1 - 29. supplementary angles with measures 10x + 7...Ch. 1.1 - 30. supplementary angles with measures 6x – 4 and...Ch. 1.1 - complementary angles with measures 9x + 6 and 3x...Ch. 1.1 - 32. complementary angles with measures 3x – 5 and...Ch. 1.1 - Find the measure of the smaller angle formed by...Ch. 1.1 - Find the measure of the smaller angle formed by...Ch. 1.1 - Find the measure of the smaller angle formed by...Ch. 1.1 - Find the measure of the smaller angle formed by...Ch. 1.1 - Find the measure of the smaller angle formed by...Ch. 1.1 - Find the measure of the smaller angle formed by...Ch. 1.1 - Perform each calculation. See Example 3. 39. 62°...Ch. 1.1 - 40. 75° 15′ + 83° 32′ Ch. 1.1 - 97 42 + 81 37Ch. 1.1 - 42. 110° 25′ + 32° 55′ Ch. 1.1 - 43. 47° 29′ – 71° 18′ Ch. 1.1 - 47 23 73 48Ch. 1.1 - 90 51 28Ch. 1.1 - 90 17 13Ch. 1.1 - 47. 180° – 119° 26′ Ch. 1.1 - 180 124 51Ch. 1.1 - 49. 90° – 72° 58′ 11″ Ch. 1.1 - 50. 90° – 36° 18′ 47″ Ch. 1.1 - Perform each calculation. See Example 3. 26 20 +...Ch. 1.1 - Perform each calculation. See Example 3. 52. 55°...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Prob. 54ECh. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Prob. 61ECh. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees....Ch. 1.1 - Convert each angle measure to decimal degrees. If...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Prob. 82ECh. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Prob. 89ECh. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Prob. 93ECh. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Find the angle of least positive measure (not...Ch. 1.1 - Prob. 96ECh. 1.1 - Give two positive and two negative angles that...Ch. 1.1 - Give two positive and two negative angles that are...Ch. 1.1 - Prob. 99ECh. 1.1 - Give two positive and two negative angles that are...Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Write an expression that generates all angles...Ch. 1.1 - Why do the answers to Exercises 107 and 108 give...Ch. 1.1 - Prob. 110ECh. 1.1 - Prob. 111ECh. 1.1 - Prob. 112ECh. 1.1 - Prob. 113ECh. 1.1 - Prob. 114ECh. 1.1 - Prob. 115ECh. 1.1 - Prob. 116ECh. 1.1 - Prob. 117ECh. 1.1 - Prob. 118ECh. 1.1 - Prob. 119ECh. 1.1 - Prob. 120ECh. 1.1 - Prob. 121ECh. 1.1 - Prob. 122ECh. 1.1 - 123. Revolutions of a Turntable A turntable in a...Ch. 1.1 - 124. Revolutions of a Windmill A windmill makes...Ch. 1.1 - Rotating Tire A tire is rotating 600 times per...Ch. 1.1 - Rotating Airplane Propeller An airplane propeller...Ch. 1.1 - Prob. 127ECh. 1.1 - Surveying One student in a surveying class...Ch. 1.1 - 129. Viewing Field of a Telescope As a...Ch. 1.1 - Angle Measure of a Star on the American Flag...Ch. 1.2 - The sum of the measures of the angles of any...Ch. 1.2 - An isosceles right triangle has one ______ angle...Ch. 1.2 - 3. An equilateral triangle has ______ equal...Ch. 1.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 1.2 - CONCEPT PREVIEW In each figure, find the measures...Ch. 1.2 - CONCEPT PREVIEW In each figure, find the measures...Ch. 1.2 - CONCEPT PREVIEW Name the corresponding angles and...Ch. 1.2 - CONCEPT PREVIEW Name the corresponding angles and...Ch. 1.2 - CONCEPT PREVIEW Name the corresponding angles and...Ch. 1.2 - CONCEPT PREVIEW Name the corresponding angles and...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Find the measure of each marked angle. In...Ch. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - Prob. 28ECh. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - The measures of two angles of a triangle are...Ch. 1.2 - 31. Concept Check Can a triangle have angles of...Ch. 1.2 - Prob. 32ECh. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Prob. 38ECh. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Prob. 40ECh. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Prob. 42ECh. 1.2 - Concept Check Classify each triangle as acute,...Ch. 1.2 - Prob. 44ECh. 1.2 - Angle Sum of a Triangle Use this figure to discuss...Ch. 1.2 - 46. Carpentry Technique The following technique...Ch. 1.2 - Find all unknown angle measures in each pair of...Ch. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Find all unknown angle measures in each pair of...Ch. 1.2 - Prob. 52ECh. 1.2 - Find the unknown side lengths in each pair of...Ch. 1.2 - Find the unknown side lengths in each pair of...Ch. 1.2 - Find the unknown side lengths in each pair of...Ch. 1.2 - Find the unknown side lengths in each pair of...Ch. 1.2 - Find the unknown side lengths in each pair of...Ch. 1.2 - Find the unknown side lengths in each pair of...Ch. 1.2 - Solve each problem. See Example 5. 59. Height of a...Ch. 1.2 - Prob. 60ECh. 1.2 - 61. Lengths of Sides of a Triangle On a photograph...Ch. 1.2 - Height of a Lighthouse The Biloxi lighthouse in...Ch. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - In each figure, there are two similar triangles....Ch. 1.2 - In each figure, there are two similar triangles....Ch. 1.2 - In each figure, there are two similar triangles....Ch. 1.2 - Prob. 68ECh. 1.2 - 69. Solar Eclipse on Earth The sun has a diameter...Ch. 1.2 - 70. Solar Eclipse on Neptune (Refer to Exercise...Ch. 1.2 - Solar Eclipse on Mars (Refer to Exercise 69.) The...Ch. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - 74. Estimates of Heights There is a relatively...Ch. 1.2 - Prob. 1QCh. 1.2 - Prob. 2QCh. 1.2 - Prob. 3QCh. 1.2 - Find the measure of each unknown angle. Ch. 1.2 - Find the measure of each unknown angle.Ch. 1.2 - Solve each problem. 6. Perform each...Ch. 1.2 - 7. Find the angle of least positive measure (not...Ch. 1.2 - Rotating Flywheel A flywheel rotates 300 times per...Ch. 1.2 - 9. Length of a Shadow If a vertical antenna 45 ft...Ch. 1.2 - Find the values of x and y.Ch. 1.3 - The Pythagorean theorem for right triangles states...Ch. 1.3 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 1.3 - 3. For any nonquadrantal angle θ, sin θ and csc θ...Ch. 1.3 - If cot is undefined, then tan =_________.Ch. 1.3 - 5. If the terminal side of an angle θ lies in...Ch. 1.3 - CONCEPT PREVIEW Fill in the blank (s) to correctly...Ch. 1.3 - CONCEPT PREVIEW The terminal side of an angle θ in...Ch. 1.3 - CONCEPT PREVIEW The terminal side of an angle in...Ch. 1.3 - CONCEPT PREVIEW The terminal side of an angle in...Ch. 1.3 - CONCEPT PREVIEW The terminal side of an angle θ in...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Prob. 24ECh. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle θ in standard position such that θ...Ch. 1.3 - Sketch an angle in standard position such that ...Ch. 1.3 - Concept Check Suppose that the point (x, y) is in...Ch. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Concept Check Suppose that the point (x, y) is in...Ch. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Concept Check Suppose that the point (x, y) is in...Ch. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - An equation of the terminal side of an angle θ in...Ch. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - Prob. 56ECh. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - An equation of the terminal side of an angle θ in...Ch. 1.3 - Prob. 61ECh. 1.3 - An equation of the terminal side of an angle in...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Prob. 66ECh. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Prob. 70ECh. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Prob. 72ECh. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Prob. 74ECh. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Prob. 78ECh. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Find the indicated function value. If it is...Ch. 1.3 - Prob. 82ECh. 1.3 - Prob. 83ECh. 1.3 - Prob. 84ECh. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Prob. 87ECh. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Prob. 92ECh. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Prob. 96ECh. 1.3 - Use trigonometric function values of quadrantal...Ch. 1.3 - Prob. 98ECh. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - Prob. 100ECh. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - Prob. 104ECh. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - Prob. 106ECh. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - If n is an integer, n 180 represents an integer...Ch. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Concept Check In later chapters we will study...Ch. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Prob. 114ECh. 1.3 - Prob. 115ECh. 1.3 - Prob. 116ECh. 1.3 - Prob. 117ECh. 1.3 - Prob. 118ECh. 1.4 - CONCEPT PREVIEW Fill in the blank(s) to...Ch. 1.4 - CONCEPT PREVIEW Fill in the blank(s) to...Ch. 1.4 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 1.4 - Prob. 4ECh. 1.4 - CONCEPT PREVIEW Determine whether each statement...Ch. 1.4 - CONCEPT PREVIEW Determine whether each...Ch. 1.4 - CONCEPT PREVIEW Determine whether each statement...Ch. 1.4 - CONCEPT PREVIEW Determine whether each statement...Ch. 1.4 - CONCEPT PREVIEW Determine whether each statement...Ch. 1.4 - CONCEPT PREVIEW Determine whether each statement...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Use the appropriate reciprocal identity to find...Ch. 1.4 - Prob. 25ECh. 1.4 - Concept Check What is wrong with the statement...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric...Ch. 1.4 - Determine the signs of the trigonometric...Ch. 1.4 - Determine the signs of the trigonometric...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Determine the signs of the trigonometric functions...Ch. 1.4 - Prob. 38ECh. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Identify the quadrant (or possible quadrants)...Ch. 1.4 - Prob. 44ECh. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Prob. 46ECh. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Prob. 48ECh. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Identify the quadrant (or possible quadrants) of...Ch. 1.4 - Prob. 51ECh. 1.4 - 52. Why is there no angle that satisfies...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Determine whether each statement is possible or...Ch. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Prob. 70ECh. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Use identities to solve each of the following....Ch. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Prob. 74ECh. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Prob. 76ECh. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Give all six trigonometric function values for...Ch. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.4 - 85. Derive the identity 1 + cot2 θ = csc2 θ by...Ch. 1.4 - 86. Derive the quotient identity . Ch. 1.4 - Concept Check True or false: For all angles , sin ...Ch. 1.4 - Prob. 88ECh. 1.4 - Concept Check Suppose that 90° < θ < 180°. Find...Ch. 1.4 - Concept Check Suppose that 90° < θ < 180°. Find...Ch. 1.4 - Prob. 91ECh. 1.4 - Prob. 92ECh. 1.4 - Concept Check Suppose that 90 180. Find the...Ch. 1.4 - Prob. 94ECh. 1.4 - Concept Check Suppose that 90° < θ < 180°. Find...Ch. 1.4 - Prob. 96ECh. 1.4 - Concept Check Suppose that –90° < θ < 90°. Find...Ch. 1.4 - Concept Check Suppose that –90° < θ < 90°. Find...Ch. 1.4 - Prob. 99ECh. 1.4 - Concept Check Suppose that –90° < θ < 90°. Find...Ch. 1.4 - Prob. 101ECh. 1.4 - Prob. 102ECh. 1.4 - Concept Check Suppose that -90 90. Find the...Ch. 1.4 - Prob. 104ECh. 1.4 - Concept Check Find a solution for each equation....Ch. 1.4 - Prob. 106ECh. 1.4 - Concept Check Find a solution for each equation....Ch. 1.4 - Concept Check Find a solution for each...Ch. 1.4 - 109. Concept Check The screen below was obtained...Ch. 1.4 - 110. Concept Check The screen below was obtained...Ch. 1 - 1. Give the measures of the complement and the...Ch. 1 - Find the angle of least positive measure that is...Ch. 1 - Find the angle of least positive measure that is...Ch. 1 - Find the angle of least positive measure that is...Ch. 1 - Rotating Propeller The propeller of a speedboat...Ch. 1 - 6. Rotating Pulley A pulley is rotating 320 times...Ch. 1 - Convert decimal degrees to degrees, minutes,...Ch. 1 - Convert decimal degrees to degrees, minutes,...Ch. 1 - Convert decimal degrees to degrees, minutes,...Ch. 1 - Convert decimal degrees to degrees, minutes,...Ch. 1 - Find the measure of each marked angle. 11. Ch. 1 - Find the measure of each marked angle.Ch. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Length of a Road A camera is located on a...Ch. 1 - 16. Express θ in terms of α and β Ch. 1 - Find all unknown angle measures in each pair of...Ch. 1 - Find all unknown angle measures in each pair of...Ch. 1 - Find the unknown side lengths in each pair of...Ch. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - 23. Length of a Shadow If a tree 20 ft tall casts...Ch. 1 - Find the six trigonometric function values for...Ch. 1 - Prob. 25RECh. 1 - Find the six trigonometric function values for...Ch. 1 - Prob. 27RECh. 1 - Find the values of the six trigonometric functions...Ch. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - An equation of the terminal side of an angle θ in...Ch. 1 - An equation of the terminal side of an angle in...Ch. 1 - An equation of the terminal side of an angle θ in...Ch. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Give all six trigonometric function values for...Ch. 1 - Give all six trigonometric function values for...Ch. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Give all six trigonometric function values for...Ch. 1 - Prob. 45RECh. 1 - Concept Check If, for some particular angle , sin ...Ch. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Height of a Lunar Peak The lunar mountain peak...Ch. 1 - 1. Give the measures of the complement and the...Ch. 1 - Prob. 2TCh. 1 - Prob. 3TCh. 1 - Prob. 4TCh. 1 - Prob. 5TCh. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Perform each conversion. 8. 74° 18′ 36″ to...Ch. 1 - Perform each conversion. 45.2025 to degrees,...Ch. 1 - Solve each problem. Find the angle of least...Ch. 1 - Prob. 11TCh. 1 - Prob. 12TCh. 1 - Prob. 13TCh. 1 - Sketch an angle θ in standard position such that...Ch. 1 - Sketch an angle in standard position such that ...Ch. 1 - Prob. 16TCh. 1 - Complete the table with the appropriate function...Ch. 1 - Prob. 18TCh. 1 - Prob. 19TCh. 1 - 20. Decide whether each statement is possible or...Ch. 1 - Find the value of sec if cos=712.Ch. 1 - Find the five remaining trigonometric function...
Knowledge Booster
Background pattern image
Trigonometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
SEE MORE TEXTBOOKS
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY