
Concept explainers
(a)
To Find:The force exerted on the strut by the hinge if the strut is weightless.
(a)
Answer to Problem 23P
Explanation of Solution
Given data:
The strut is weightless.
Weight of the block, 60 N
Formula used:
Static
Calculation:
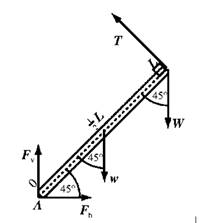
The force exerted on the strut at the hinge:
Ignore the weight of the strut and use
Use
Solve for
Solve for
Subtitute in equation
Conclusion:
(b)
The force exerted on the strut by the hinge if the strut weighs
(b)
Answer to Problem 23P
Explanation of Solution
Given data:
Strut weighs,
Weight of the block, 60 N
Formula used:
Translational and
Calculation:
Including the weight of the strut, apply
Apply
And
Solve for
Solver for
Substitute in equation
Conclusion:
Want to see more full solutions like this?
Chapter 12 Solutions
Physics for Scientists and Engineers
- A worker lifts a box under the following conditions:Horizontal distance (H): 30 cmInitial height (V): 60 cmVertical travel (D): 50 cmTorso rotation (A): 30°Frequency: 3 times/minute for 1 hourGrip: Good Question:What is the RWL for this task?What does this value mean in terms of occupational safety?arrow_forwardCan someone helparrow_forwardCan someone help mearrow_forward
- 3. Four identical small masses are connected in a flat perfect square. Rank the relative rotational inertias (IA, IB, IC) about the three axes of rotation shown. Axes A and B are in the plane of the square, and axis C is perpendicular to the plane, through mass m1. ΙΑ IB m2 m1 m3 Ic m4 (a) IAarrow_forwardConsider the circuit shown in the figure below. (Assume L = 5.20 m and R2 = 440 Ω.) (a) When the switch is in position a, for what value of R1 will the circuit have a time constant of 15.4 µs? (b) What is the current in the inductor at the instant the switch is thrown to position b?arrow_forwardCan someone helparrow_forwardCan someone help mearrow_forwardA particle in a box between x=0 and x=6 has the wavefunction Psi(x)=A sin(2πx). How muchenergy is required for the electron to make a transition to Psi(x)= A’ sin(7π x/3). Draw anapproximate graph for the wavefunction. Find A and A'arrow_forwardA proton is moving with 10^8 m/s speed. Find the De Broglie wavelength associated with theproton and the frequency of that wave.arrow_forwardFind the wavelength of the photon if a (Li--) electron makes a transition from n=4 to n=3. Findthe Bohr radius for each state.arrow_forwardA photon with wavelength 3000 nm hits a stationary electron. After the collision electron isscattered to 60 degrees. Find the wavelength and frequency of the scattered photon.arrow_forwardA metal has threshold frequency 10^15. Calculate the maximum kinetic energy of the ejectedelectron if a laser beam with wavelength 1.5 10^-7 m is projected on the metal.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





