Chapter 12, Problem 21P

To determine

Find the approximate axial forces, shears, and moments for the all members of the frames using cantilever method.

Explanation of Solution

Given information:

The axial force acting at point M $\left(H_M\right)$ is 7.5 k.

The axial force acting at point I $\left(H_I\right)$ is 15 k.

The axial force acting at point E $\left(H_E\right)$ is 15 k.

The vertical distance of the member JM and KL $\left(L_1\right)$ is 16 ft.

The vertical distance of the member EI, FJ, GK, and HL $\left(L_2\right)$ is 16 ft.

The vertical distance of the member AE, BF, CG, and DH $\left(L_3\right)$ is 16 ft.

The horizontal distance of the members AB, EF, and IJ $\left(l_1\right)$ is 30 ft.

The horizontal distance of the members BC, FG, and JK $\left(l_2\right)$ is 20 ft.

The horizontal distance of the members CD, GH, and KL $\left(l_3\right)$ is 30 ft.

Take the counterclockwise moment is positive and clockwise moment is negative.

The axial force in horizontal direction, towards right is positive and towards left side is negative.

The axial force in vertical direction, towards upward is positive and towards downward is negative.

Calculation:

Insert the internal hinges at the midpoints of all the members of the given frame to obtain the simplified frame for approximate analysis.

Draw the simplified frame as in Figure (1).

For the calculation of column axial forces of story of the frame, pass an imaginary section aa through the internal hinges at the midheights of columns JM and KN, pass an imaginary section bb through the internal hinges at the midheights of columns EI, FJ, GK, and HL, and pass an imaginary section cc through the internal hinges at the midheights of columns AE, BF, CG, and DH.

Draw the free body diagram of the frame portion with the passed imaginary lines as in Figure (2).

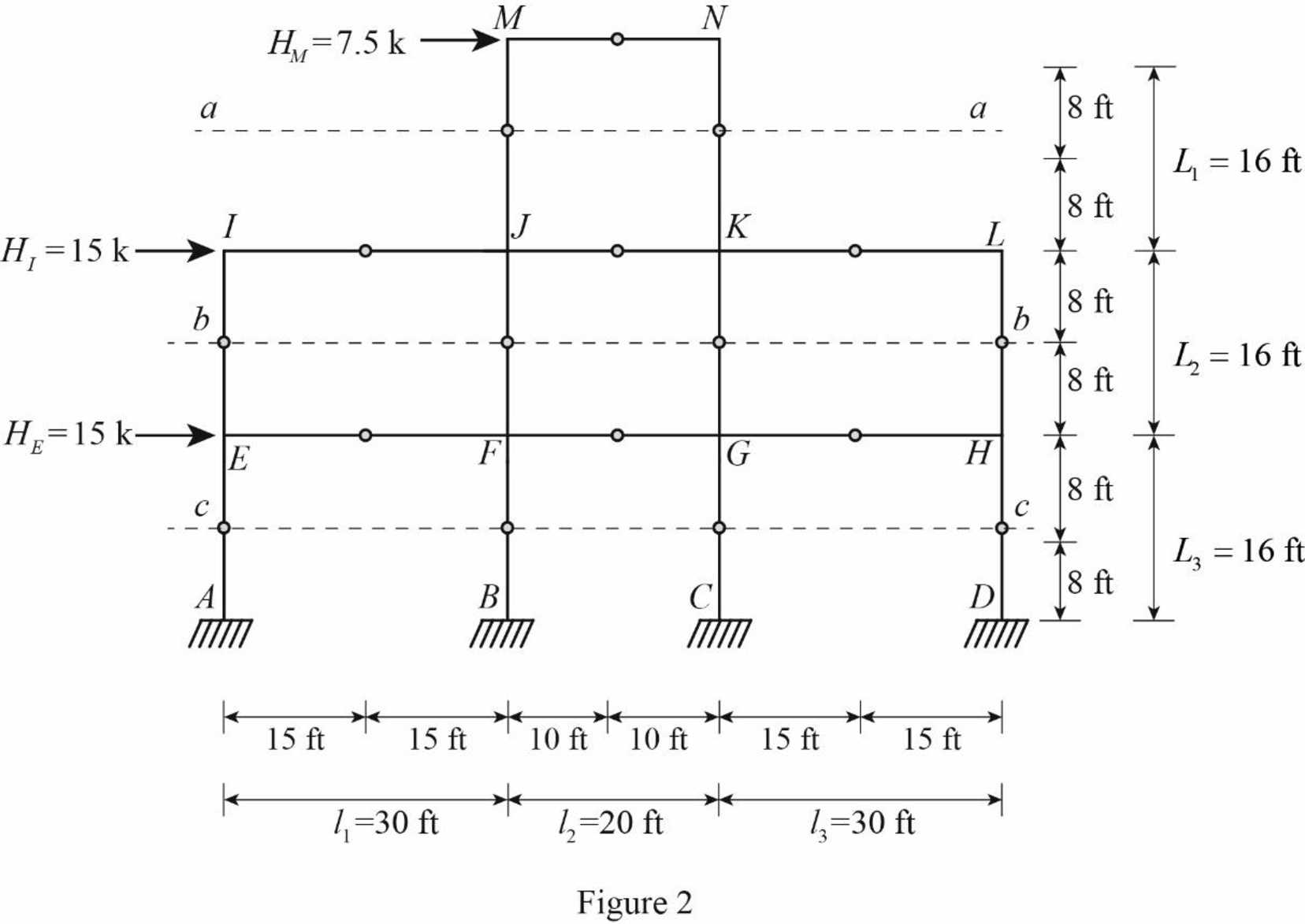
Column axial forces:

Above section aa:

Draw the free body diagram of the frame portion above the section aa as in Figure (3).

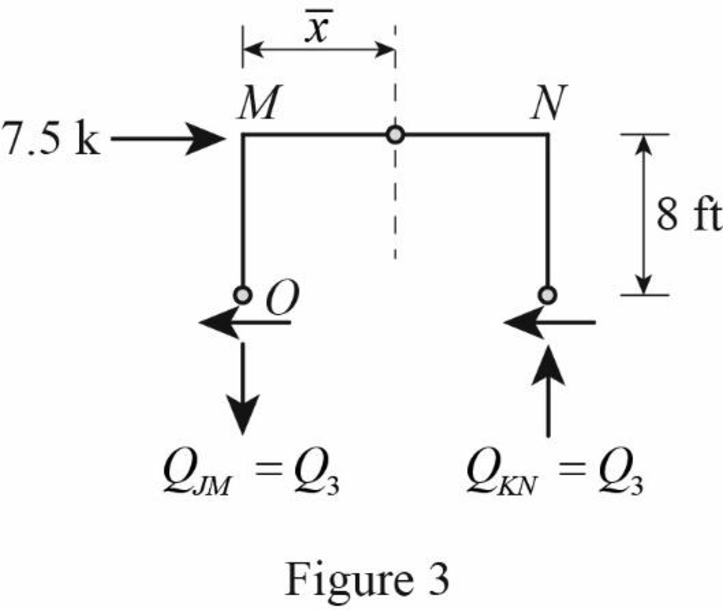
Determine the location of the centroid from support A using the relation.

$\begin{array}{c}\overline{x}=\frac{{\displaystyle \sum Ax}}{{\displaystyle \sum A}}\\ =\frac{{\displaystyle \sum A{x}_1+A{x}_2+A{x}_3+A{x}_4}}{4A}\end{array}$        (1)

Here, A is the area of the column sections, $x_1$ is the initial distance, $x_2$ is the distance for the support B from support A, $x_3$ is the distance for the support C from support A, and $x_4$ is the distance for the support D from support A.

Substitute 0 ft for $x_1$, 30 ft for $x_2$, 50 ft for $x_3$, and 80 ft for $x_4$ in Equation (1).

$\begin{array}{c}\overline{x}=\frac{A\left(0\right)+A\left(30\right)+A\left(50\right)+A\left(80\right)}{4A}\\ =40\text{ft}\end{array}$

The location of the centroid from the column member JM is 10 ft.

The given lateral load is acting on the frame to the right, therefore the axial force in column JM located to the left of the centroid, must be tensile whereas the axial force in column KN placed to the right of the centroid, must be compressive.

Determine the axial force in the column members JM and KN using equilibrium conditions.

Take moment about point O.

$\begin{array}{l}{\displaystyle \sum M_O}=0\\ Q_3\times l_2-H_M\times \frac{L_1}{2}=0\end{array}$

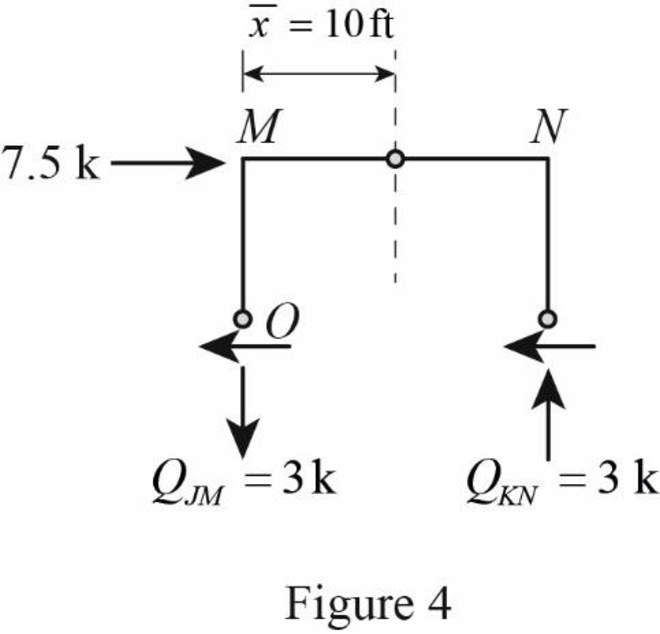
Substitute 20 ft for $l_2$, 20 k for $H_M$, and 16 ft for $L_1$.

$\begin{array}{l}{Q}_3\times 20-7.5\times \frac{16}{2}=0\\ 20Q_3=60\\ Q_3=\frac{60}{20}\\ Q_3=3\text{k}\end{array}$

The axial force in the column members JM and KN is $Q_{JM}=3\text{k}(\downarrow )$ and $Q_{KN}=3\text{k}(\uparrow )$.

Draw the free body diagram of the frame portion above the section aa with the axial forces in the column members as in Figure (4).

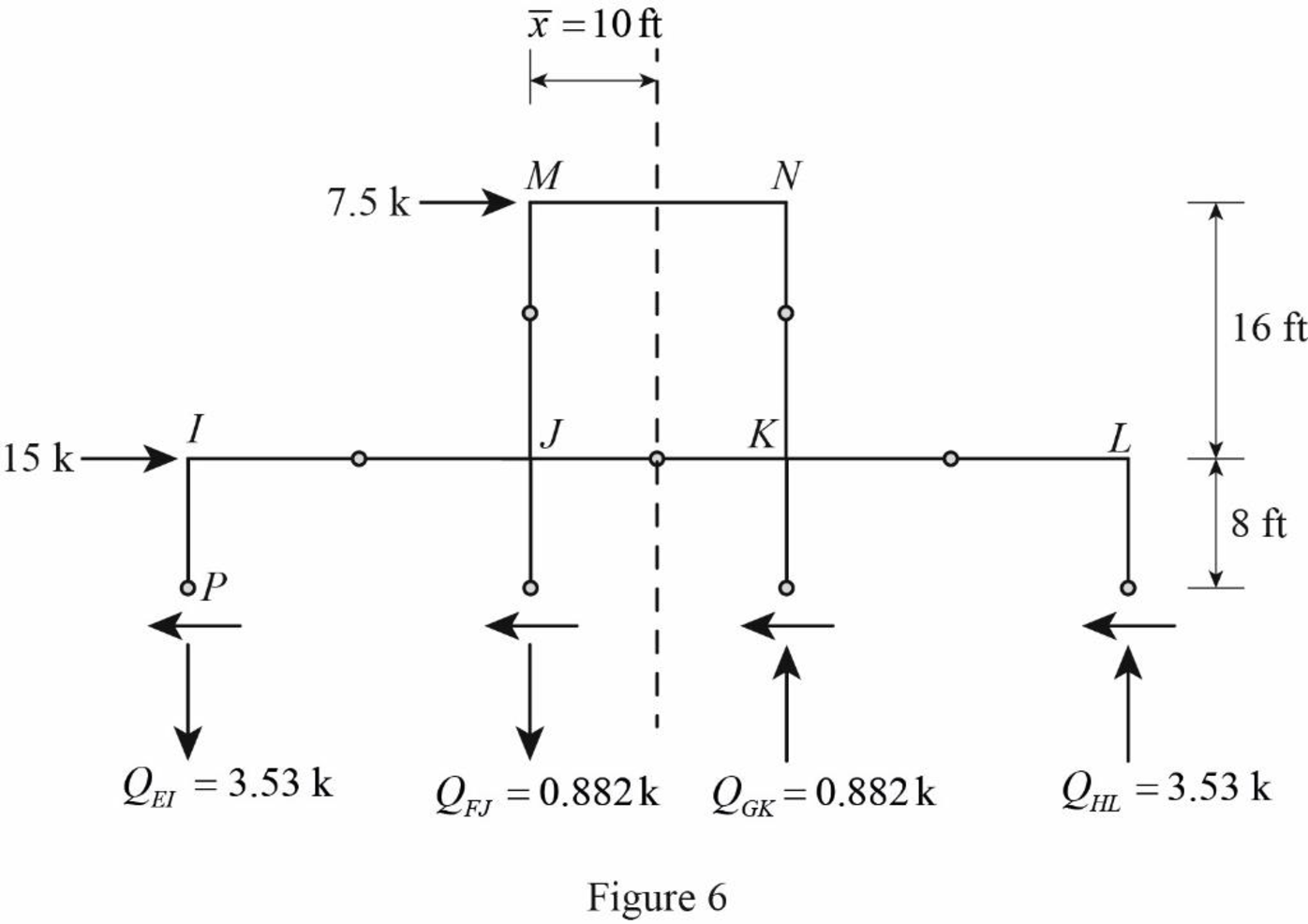
Draw the free body diagram of the frame portion above the section bb as in Figure (5).

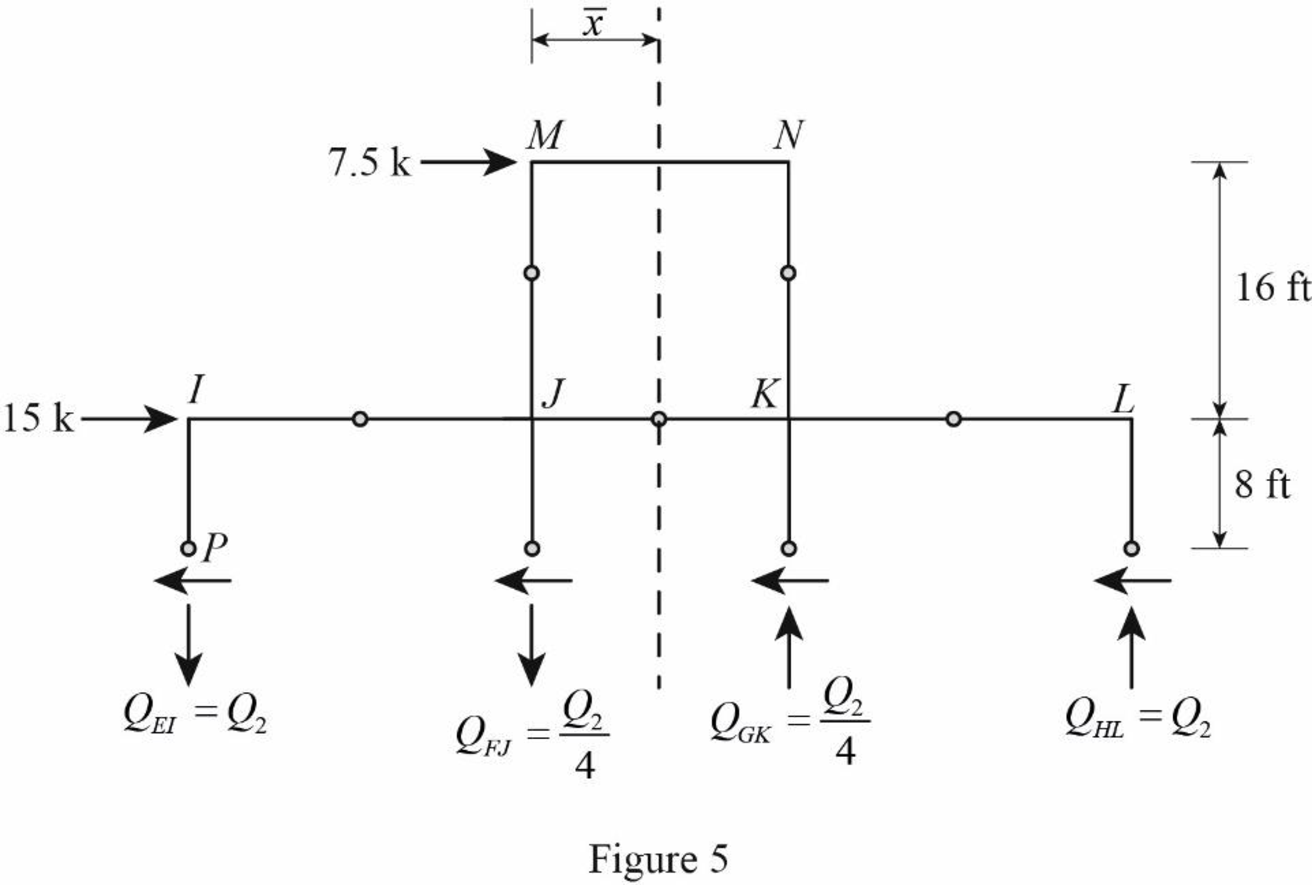
Consider the axial forces in the columns are to be linearly proportional to their distances from centroid.

The given lateral load is acting on the frame to the right, therefore the axial force in column EI and FJ located to the left of the centroid, must be tensile whereas the axial force in column GK and HL placed to the right of the centroid, must be compressive.

Refer Figure (5).

Determine the relationship in column axial force between the member EI and FJ using the relation.

$Q_{FJ}=\frac{\overline{x}-l_1}{\overline{x}}{Q}_{EI}$

Substitute 40 ft for $\overline{x}$ and 30 ft for $l_1$.

$\begin{array}{c}{Q}_{FJ}=\frac{40-30}{40}{Q}_{EI}\\ =\frac{10}{40}{Q}_{EI}\\ =\frac{Q_{EI}}{4}\end{array}$

Determine the relationship in column axial force between the member EI and GK using the relation.

$Q_{GK}=\frac{\left(l_1+l_2\right)-\overline{x}}{\overline{x}}{Q}_{EI}$

Substitute 30 ft for $l_1$, 20 ft for $l_2$, and 40 ft for $\overline{x}$.

$\begin{array}{c}{Q}_{GK}=\frac{\left(30+20\right)-40}{40}{Q}_{EI}\\ =\frac{10}{40}{Q}_{EI}\\ =\frac{Q_{EI}}{4}\end{array}$

Determine the axial force in the column members EI, FJ, GK, and HL using equilibrium conditions.

Take moment about point P.

$\begin{array}{l}{\displaystyle \sum M_P}=0\\ Q_{HL}\times \left(l_1+l_2+l_3\right)+Q_{GK}\times \left(l_1+l_2\right)-Q_{FJ}\times l_1-H_M\times \left(L_1+\frac{L_2}{2}\right)-H_I\times \frac{L_2}{2}=0\end{array}$

Substitute $Q_{EI}$ for $Q_{HL}$, 30 ft for $l_1$, 20 ft for $l_2$, 30 ft for $l_3$, $\frac{Q_{EI}}{4}$ for $Q_{GK}$, $\frac{Q_{EI}}{4}$ for $Q_{FJ}$, 7.5 k for $H_M$, 16 ft for $L_1$, 15 k for $H_I$, and 16 ft for $L_2$.

$\begin{array}{l}{Q}_{EI}\times \left(30+20+30\right)+\frac{1}{4}{Q}_{EI}\times \left(20+30\right)-\frac{1}{4}{Q}_{EI}\times 30-7.5\times \left(16+\frac{16}{2}\right)-15\times \frac{16}{2}=0\\ 80Q_{EI}+\frac{50}{4}{Q}_{EI}-\frac{30}{4}{Q}_{EI}=300\\ Q_{EI}=\frac{300}{85}\\ Q_{EI}=3.53\text{k}\end{array}$

Determine the axial force in the column members FJ.

$Q_{FJ}=\frac{1}{4}{Q}_{EI}$

Substitute 3.53 k for $Q_{EI}$.

$\begin{array}{c}{Q}_{FJ}=\frac{1}{4}\times 3.53\\ =0.882\text{k}(\downarrow )\end{array}$

Determine the axial force in the column members GK.

$Q_{GK}=\frac{1}{4}{Q}_{EI}$

Substitute 3.53 k for $Q_{EI}$.

$\begin{array}{c}{Q}_{GK}=\frac{1}{4}\times 3.53\\ =0.882\text{k}(\uparrow )\end{array}$

Determine the axial force in the column members HL.

$Q_{HL}=Q_{EI}$

Substitute 3.53 k for $Q_{EI}$.

$Q_{HL}=3.53\text{k}(\uparrow )$

Draw the free body diagram of the frame portion above the section bb with the axial forces in the column members as in Figure (6).

Draw the free body diagram of the frame portion above the section cc as in Figure (7).

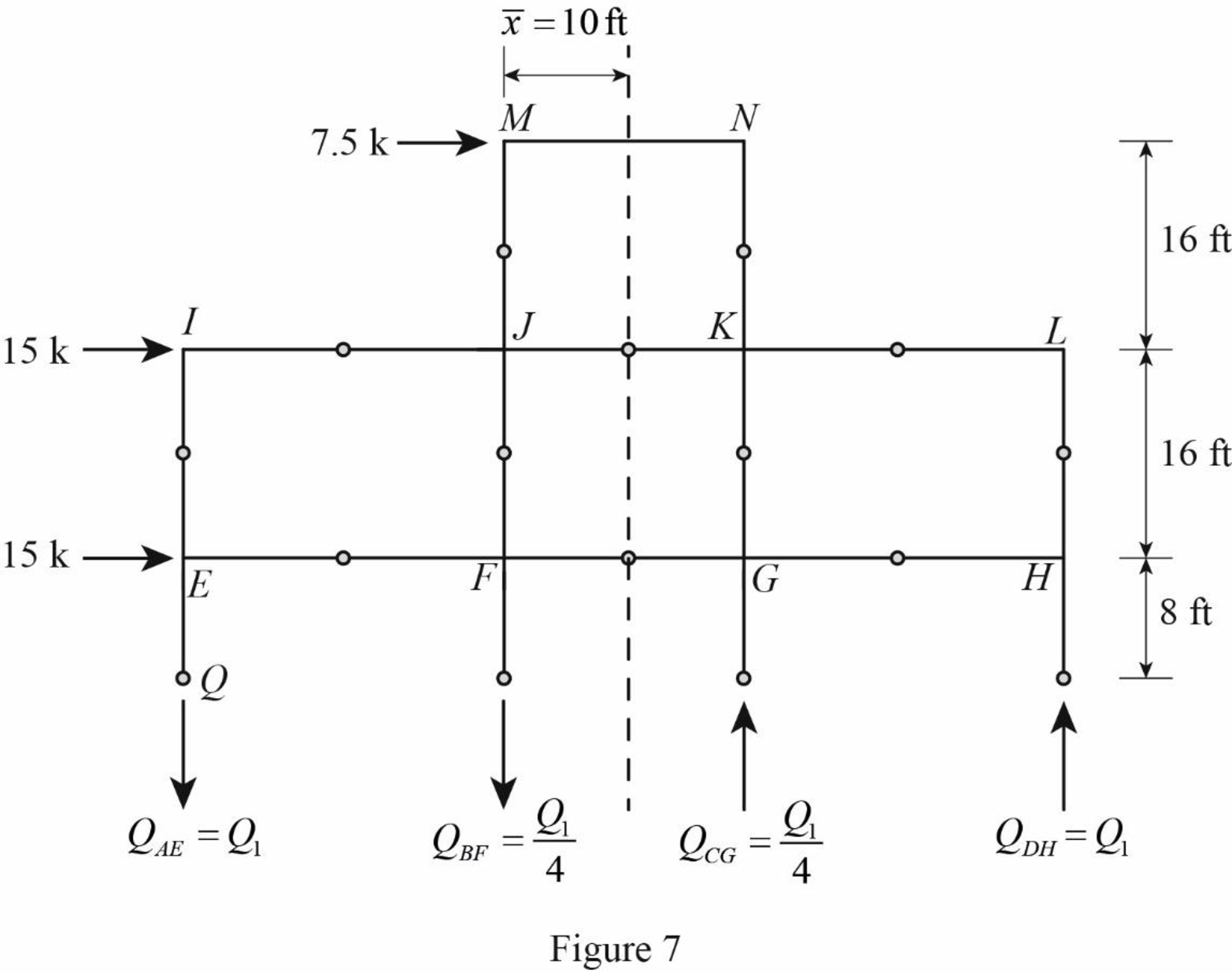
The given lateral load is acting on the frame to the right, therefore the axial force in column AE and BF located to the left of the centroid, must be tensile, whereas the axial force in column CG and DH placed to the right of the centroid, must be compressive.

Determine the relationship in column axial force between the member AE and BF using the relation.

$Q_{BF}=\frac{\overline{x}-l_1}{\overline{x}}{Q}_{AE}$

Substitute 40 ft for $\overline{x}$ and 30 ft for $l_1$.

$\begin{array}{c}{Q}_{BF}=\frac{40-30}{40}{Q}_{AE}\\ =\frac{10}{40}{Q}_{AE}\\ =\frac{Q_{AE}}{4}\end{array}$

Determine the relationship in column axial force between the member AE and CG using the relation.

$Q_{CG}=\frac{\left(l_1+l_2\right)-\overline{x}}{\overline{x}}{Q}_{AE}$

Substitute 30 ft for $l_1$, 20 ft for $l_2$, and 40 ft for $\overline{x}$.

$\begin{array}{c}{Q}_{CG}=\frac{\left(30+20\right)-40}{40}{Q}_{AE}\\ =\frac{10}{40}{Q}_{AE}\\ =\frac{Q_{AE}}{4}\end{array}$

Determine the axial force in the column members AE, BF, CG, and DH using equilibrium conditions.

Take moment about point Q.

$\begin{array}{l}{\displaystyle \sum M_Q}=0\\ \left\{\begin{array}{l}{Q}_{DH}\times \left(l_1+l_2+l_3\right)+Q_{CG}\times \left(l_1+l_2\right)-Q_{BF}\times l_1-H_M\times \left(L_1+L_2+\frac{L_3}{2}\right)\\ -H_I\times \left(L_2+\frac{L_3}{2}\right)-H_E\times \frac{L_3}{2}\end{array}\right\}=0\end{array}$

Substitute $Q_{AE}$ for $Q_{DH}$, 30 ft for $l_1$, 20 ft for $l_2$, 30 ft for $l_3$, $\frac{Q_{AE}}{4}$ for $Q_{CG}$, $\frac{Q_{AE}}{4}$ for $Q_{BF}$, 7.5 k for $H_M$, 16 ft for $L_1$, 16 ft for $L_2$, 16 ft for $L_3$, 15 k for $H_I$, and 15 k for $H_E$.

$\begin{array}{l}\left\{\begin{array}{l}{Q}_{AE}\times \left(30+20+30\right)+\frac{1}{4}{Q}_{AE}\times \left(20+30\right)-\frac{1}{4}{Q}_{AE}\times 30-\\ 7.5\times \left(16+16+\frac{16}{2}\right)-15\times \left(16+\frac{16}{2}\right)-15\times \frac{16}{2}\end{array}\right\}=0\\ 80Q_{AE}+\frac{50}{4}{Q}_{AE}-\frac{30}{4}{Q}_{AE}=780\\ Q_{AE}=\frac{780}{85}\\ Q_{AE}=9.18\text{k}(\downarrow )\end{array}$

Determine the axial force in the column members BF.

$Q_{BF}=\frac{1}{4}{Q}_{AE}$

Substitute 9.18 k for $Q_{AE}$.

$\begin{array}{c}{Q}_{BF}=\frac{1}{4}\times 9.18\\ =2.29\text{k}(\downarrow )\end{array}$

Determine the axial force in the column members CG.

$Q_{CG}=\frac{1}{4}{Q}_{AE}$

Substitute 9.18 k for $Q_{AE}$.

$\begin{array}{c}{Q}_{CG}=\frac{1}{4}\times 9.18\\ =2.29\text{k}(\uparrow )\end{array}$

Determine the axial force in the column members DH.

$Q_{DH}=Q_{AE}$

Substitute 2.29 k for $Q_{AE}$.

$Q_{DH}=2.29\text{k}(\uparrow )$

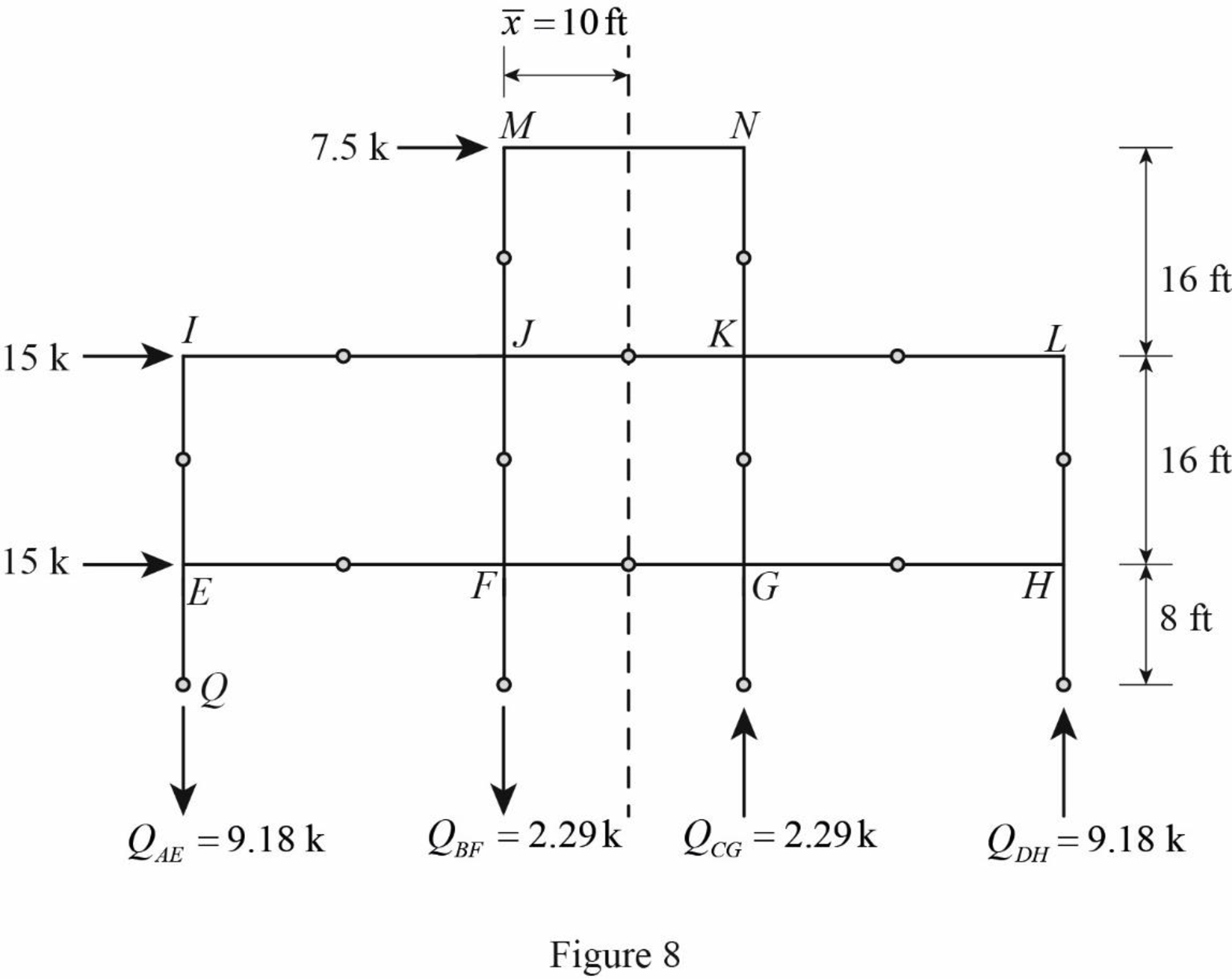
Draw the free body diagram of the frame portion above the section bb with the axial forces in the column members as in Figure (8).

Girder shear and moments:

Consider girder MN.

Determine the shear at upper left end joint M using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{MN}-Q_{JM}=0\end{array}$

Substitute 3 k for $Q_{JM}$.

$\begin{array}{l}{S}_{MN}+3=0\\ S_{MN}=-3\text{k}\\ S_{MN}=3\text{k}(\downarrow )\end{array}$

Determine the shear at upper right end joint N using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{MN}+S_{NM}=0\end{array}$

Substitute 3 k for $S_{NM}$.

$\begin{array}{l}-3+S_{NM}=0\\ S_{NM}=3\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder MN using equilibrium equations.

$M_{MN}=-S_{MN}\times \frac{l_2}{2}$

Substitute 3 k for $S_{MN}$ and 20 ft for $l_2$.

$\begin{array}{c}{M}_{MN}=-3\times \frac{20}{2}\\ =30\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder NM using equilibrium equations.

Take moment about point M.

$\begin{array}{l}{\displaystyle \sum M_M=0}\\ -M_{MN}+S_{NM}\times l_2+M_{NM}=0\end{array}$

Substitute $30\text{k-ft}$ for $M_{MN}$, 3 k for $S_{NM}$, and 20 ft for $l_2$.

$\begin{array}{l}-30+3\times 20+M_{NM}=0\\ M_{NM}=-30\text{k-ft}\\ M_{NM}=30\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Consider girder IJ.

Determine the shear at upper left end joint I using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{IJ}+Q_{IE}=0\end{array}$

Substitute 3.53 k for $Q_{IE}$.

$\begin{array}{l}{S}_{IJ}+3.53=0\\ S_{IJ}=-3.53\text{k}\\ S_{IJ}=3.53\text{k}(\downarrow )\end{array}$

Determine the shear at upper right end joint J using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{IJ}+S_{JI}=0\end{array}$

Substitute 3.53 k for $S_{IJ}$.

$\begin{array}{l}-3.53+S_{JI}=0\\ S_{JI}=3.53\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder IJ using equilibrium equations.

$M_{IJ}=-S_{IJ}\times \frac{l_1}{2}$

Substitute 3.53 k for $S_{IJ}$ and 30 ft for $l_1$.

$\begin{array}{c}{M}_{IJ}=-3.53\times \frac{30}{2}\\ \approx 53\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder IJ using equilibrium equations.

Take moment about point I.

$\begin{array}{l}{\displaystyle \sum M_I=0}\\ -M_{IJ}+S_{JI}\times l_1+M_{JI}=0\end{array}$

Substitute $53\text{k-ft}$ for $M_{IJ}$, 3.53 k for $S_{JI}$, and 30 ft for $l_1$.

$\begin{array}{l}-53+3.53\times 30+M_{JI}=0\\ M_{JI}=-53\text{k-ft}\\ M_{JI}=53\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Consider girder JK.

Determine the shear at left end joint J using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{JI}+S_{JK}+Q_{JF}-Q_{JM}=0\end{array}$

Substitute 3.53 k for $S_{JI}$, 0.882 k for $Q_{JF}$, and 3 k for $Q_{JM}$.

$\begin{array}{l}3.53+S_{JK}+0.882-3=0\\ S_{JK}=-1.41\text{k}\\ S_{JK}=1.41\text{k}(\downarrow )\end{array}$

Determine the shear at right end joint K using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{JK}+S_{KJ}=0\end{array}$

Substitute 1.41 k for $S_{JK}$.

$\begin{array}{l}-1.41+S_{JK}=0\\ S_{JK}=1.41\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder JK using equilibrium equations.

$M_{JK}=-S_{JK}\times \frac{l_2}{2}$

Substitute 1.41 k for $S_{JK}$ and 20 ft for $l_2$.

$\begin{array}{c}{M}_{JK}=-1.41\times \frac{20}{2}\\ =-14.1\text{k-ft}\\ =14.1\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder JK using equilibrium equations.

Take moment about point J.

$\begin{array}{l}{\displaystyle \sum M_J=0}\\ -M_{JK}+S_{KJ}\times l_2+M_{KJ}=0\end{array}$

Substitute $14.1\text{k-ft}$ for $M_{JK}$, 1.41 k for $S_{KJ}$, and 20 ft for $l_2$.

$\begin{array}{l}-14.1+1.41\times 20+M_{KJ}=0\\ M_{KJ}=-14.1\text{k-ft}\\ M_{KJ}=14.1\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Consider girder KL.

Determine the shear at left end joint K using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{KJ}+S_{KL}-Q_{KG}+Q_{KN}=0\end{array}$

Substitute 1.41 k for $S_{KJ}$, 0.882 k for $Q_{KG}$, and 3 k for $Q_{KN}$.

$\begin{array}{l}1.41+S_{KL}-0.882+3=0\\ S_{KL}=-3.53\text{k}\\ S_{KL}=3.53\text{k}(\downarrow )\end{array}$

Determine the shear at right end joint L using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{KL}+S_{LK}=0\end{array}$

Substitute 3.53 k for $S_{KL}$.

$\begin{array}{l}-3.53+S_{KL}=0\\ S_{KL}=3.53\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder KL using equilibrium equations.

$M_{KL}=-S_{KL}\times \frac{l_3}{2}$

Substitute 3.53 k for $S_{KL}$ and 30 ft for $l_3$.

$\begin{array}{c}{M}_{KL}=-3.53\times \frac{30}{2}\\ \approx -53\text{k-ft}\\ =53\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder JK using equilibrium equations.

Take moment about point K.

$\begin{array}{l}{\displaystyle \sum M_K=0}\\ -M_{KL}+S_{LK}\times l_3+M_{LK}=0\end{array}$

Substitute $53\text{k-ft}$ for $M_{JK}$, 3.53 k for $S_{LK}$, and 30 ft for $l_3$.

$\begin{array}{l}-53+3.53\times 30+M_{LK}=0\\ M_{LK}=-53\text{k-ft}\\ M_{LK}=53\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Consider girder EF.

Determine the shear at left end joint E using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{EF}-Q_{EI}+Q_{EA}=0\end{array}$

Substitute 3.53 k for $Q_{EI}$ and 9.18 k for $Q_{EA}$.

$\begin{array}{l}{S}_{EF}-3.53+9.18=0\\ S_{EF}=-5.65\text{k}\\ S_{EF}=5.65\text{k}(\downarrow )\end{array}$

Determine the shear at right end joint F using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{EF}+S_{FE}=0\end{array}$

Substitute 5.65 k for $S_{EF}$.

$\begin{array}{l}-5.65+S_{FE}=0\\ S_{FE}=5.65\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder EF using equilibrium equations.

$M_{EF}=-S_{EF}\times \frac{l_1}{2}$

Substitute 5.65 k for $S_{EF}$ and 30 ft for $l_1$.

$\begin{array}{c}{M}_{EF}=-5.65\times \frac{30}{2}\\ =-84.75\text{k-ft}\\ =84.75\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder EF using equilibrium equations.

Take moment about point E.

$\begin{array}{l}{\displaystyle \sum M_E=0}\\ -M_{EF}+S_{FE}\times l_1+M_{FE}=0\end{array}$

Substitute $84.75\text{k-ft}$ for $M_{EF}$, 5.65 k for $S_{FE}$, and 30 ft for $l_1$.

$\begin{array}{l}-84.75+5.65\times 30+M_{FE}=0\\ M_{FE}=-84.75\text{k-ft}\\ M_{FE}=84.75\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Consider girder FG.

Determine the shear at left end joint F using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{FE}+S_{FG}-Q_{FJ}+Q_{FB}=0\end{array}$

Substitute 5.65 k for $S_{FE}$, 0.882 k for $Q_{FJ}$, and 2.29 k for $Q_{FB}$.

$\begin{array}{l}5.65+S_{FG}-0.882+2.29=0\\ S_{FG}=-7.06\text{k}\\ S_{FG}\text{=}7.06\text{k}(\downarrow )\end{array}$

Determine the shear at right end joint G using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{FG}+S_{GF}=0\end{array}$

Substitute 7.06 k for $S_{FG}$.

$\begin{array}{l}-7.06+S_{GF}=0\\ S_{GF}=7.06\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder FG using equilibrium equations.

$M_{FG}=-S_{FG}\times \frac{l_2}{2}$

Substitute 7.06 k for $S_{FG}$ and 20 ft for $l_2$.

$\begin{array}{c}{M}_{FG}=-7.06\times \frac{20}{2}\\ =-70.6\text{k-ft}\\ =70.6\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder FG using equilibrium equations.

Take moment about point F.

$\begin{array}{l}{\displaystyle \sum M_F=0}\\ -M_{FG}+S_{GF}\times l_2+M_{GF}=0\end{array}$

Substitute $70.6\text{k-ft}$ for $M_{FG}$, 7.06 k for $S_{GF}$, and 20 ft for $l_2$.

$\begin{array}{l}-70.6+7.06\times 20+M_{GF}=0\\ M_{GF}=-70.6\text{k-ft}\\ M_{GF}=70.6\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Consider girder GH.

Determine the shear at left end joint G using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ S_{GH}+S_{GF}+Q_{GK}-Q_{GC}=0\end{array}$

Substitute 7.06 k for $S_{GF}$, 0.882 k for $Q_{GK}$, and 2.29 k for $Q_{GC}$.

$\begin{array}{l}{S}_{GH}+7.06+0.882-2.29=0\\ S_{GH}=-5.65\text{k}\\ S_{GH}=5.65\text{k}(\downarrow )\end{array}$

Determine the shear at right end joint H using equilibrium equation.

$\begin{array}{l}{\displaystyle \sum F_Y}=0\\ -S_{GH}+S_{HG}=0\end{array}$

Substitute 5.65 k for $S_{GH}$.

$\begin{array}{l}-5.65+S_{HG}=0\\ S_{HG}=5.65\text{k}(\uparrow )\end{array}$

Determine the moment at left end of the girder GH using equilibrium equations.

$M_{GH}=-S_{GH}\times \frac{l_3}{2}$

Substitute 5.65 k for $S_{GH}$ and 30 ft for $l_3$.

$\begin{array}{c}{M}_{GH}=-5.65\times \frac{30}{2}\\ =-84.75\text{k-ft}\\ =84.75\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Determine the moment at right end of the girder GH using equilibrium equations.

Take moment about point G.

$\begin{array}{l}{\displaystyle \sum M_G=0}\\ -M_{GH}+S_{HG}\times l_3+M_{HG}=0\end{array}$

Substitute $84.75\text{k-ft}$ for $M_{GH}$, 5.65 k for $S_{HG}$, and 30 ft for $l_3$.

$\begin{array}{l}-84.75+5.65\times 30+M_{HG}=0\\ M_{HG}=-84.75\text{k-ft}\\ M_{HG}=84.75\text{k-ft}\left(\text{Clockwise}\right)\end{array}$

Column moments and shears:

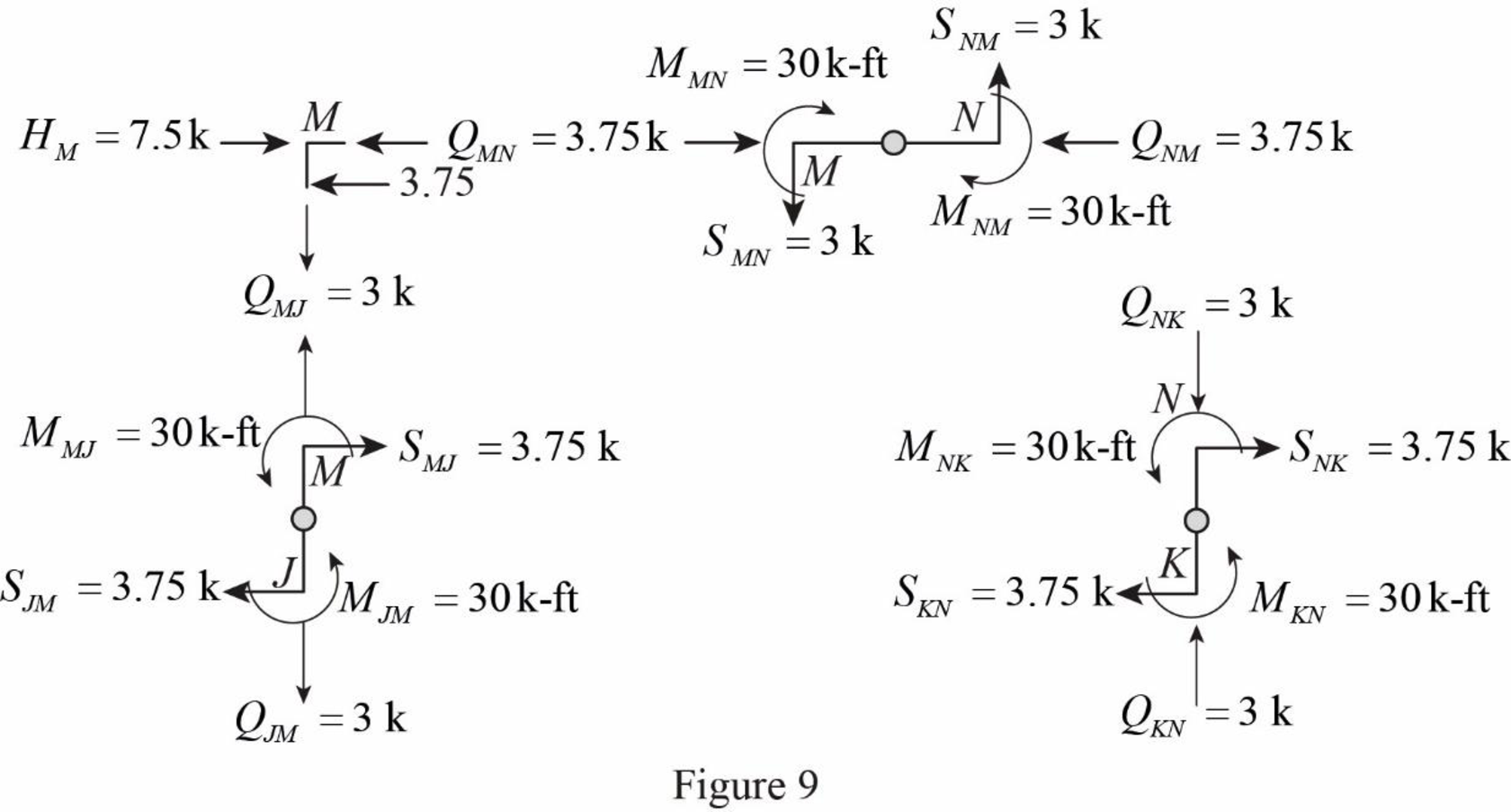
Column moment for member JM and KN:

Determine the moment at the column member JM using moment equilibrium of joints.

Apply the moment equilibrium of joints at M.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{MJ}-M_{MN}=0\end{array}$

Substitute $30\text{k-ft}$ for $M_{MN}$.

$\begin{array}{l}{M}_{MJ}-30=0\\ M_{MJ}=30\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member JM is $M_{JM}=M_{MJ}=30\text{k-ft}\left(\text{Counterclockwise}\right)$.

Determine the moment at the column member KN using moment equilibrium of joints.

Apply the moment equilibrium of joints at N.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{NK}-M_{NM}=0\end{array}$

Substitute $30\text{k-ft}$ for $M_{NM}$.

$\begin{array}{l}{M}_{NK}-30=0\\ M_{NK}=30\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member KN is $M_{KN}=M_{NK}=30\text{k-ft}\left(\text{Counterclockwise}\right)$.

Column shear for member JM and KN:

Determine the shear at the end M in the column member JM using the relation.

$S_{MJ}=\frac{M_{MJ}}{\frac{L_1}{2}}$

Substitute $30\text{k-ft}$ for $M_{MJ}$ and 16 ft for $L_1$.

$\begin{array}{c}{S}_{MJ}=\frac{30}{\frac{16}{2}}\\ =3.75\text{k}(\to )\end{array}$

The shear at the column member MJ must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint M.

Determine the shear at the end of the column J using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{MJ}+S_{JM}=0\end{array}$

Substitute 3.75 k for $S_{MJ}$.

$\begin{array}{l}3.75+S_{JM}=0\\ S_{JM}=-3.75\text{k}\\ S_{JM}=3.75\text{k}(\leftarrow )\end{array}$

Determine the shear at the end N in the column member KN using the relation.

$S_{NK}=\frac{M_{NK}}{\frac{L_1}{2}}$

Substitute $30\text{k-ft}$ for $M_{NK}$ and 16 ft for $L_1$.

$\begin{array}{c}{S}_{NK}=\frac{30}{\frac{16}{2}}\\ =3.75\text{k}(\to )\end{array}$

The shear at the column member NK must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint N.

Determine the shear at the end of the column K using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{NK}+S_{KN}=0\end{array}$

Substitute 3.75 k for $S_{NK}$.

$\begin{array}{l}3.75+S_{KN}=0\\ S_{KN}=-3.75\text{k}\\ S_{KN}=3.75\text{k}(\leftarrow )\end{array}$

Column moment for member EI, FJ, GK, and HL:

Determine the moment at the column member EI using moment equilibrium of joints.

Apply the moment equilibrium of joints at I.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{IE}-M_{IJ}=0\end{array}$

Substitute $53\text{k-ft}$ for $M_{IJ}$.

$\begin{array}{l}{M}_{IE}-53=0\\ M_{IE}=53\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member EI is $M_{EI}=M_{IE}=53\text{k-ft}\left(\text{Counterclockwise}\right)$.

Determine the moment at the column member FJ.

Apply the moment equilibrium of joints at J.

$\begin{array}{l}{\displaystyle \sum M=0}\\ -M_{JI}-M_{JK}+M_{JF}+M_{JM}=0\end{array}$

Substitute $53\text{k-ft}$ for $M_{JI}$, $14.1\text{k-ft}$ for $M_{JK}$, and $30\text{k-ft}$ for $M_{JM}$.

$\begin{array}{l}-53-14.1+M_{JF}+30=0\\ M_{JF}=37.1\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member FJ is $M_{JF}=M_{FJ}=37.1\text{k-ft}\left(\text{Counterclockwise}\right)$.

Determine the moment at the column member GK.

Apply the moment equilibrium of joints at K.

$\begin{array}{l}{\displaystyle \sum M=0}\\ -M_{KJ}-M_{KL}+M_{KG}+M_{KN}=0\end{array}$

Substitute $14.1\text{k-ft}$ for $M_{KJ}$, $53\text{k-ft}$ for $M_{KL}$, and $30\text{k-ft}$ for $M_{KN}$.

$\begin{array}{l}-14.1-53+M_{KG}+30=0\\ M_{KG}=37.1\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member GK is $M_{KG}=M_{GK}=37.1\text{k-ft}\left(\text{Counterclockwise}\right)$.

Determine the moment at the column member HL using moment equilibrium of joints.

Apply the moment equilibrium of joints at L.

$\begin{array}{l}{\displaystyle \sum M=0}\\ -M_{LK}+M_{LH}=0\end{array}$

Substitute $53\text{k-ft}$ for $M_{LK}$.

$\begin{array}{l}-53+M_{LH}=0\\ M_{LH}=53\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member IF is $M_{LH}=M_{HL}=53\text{k-ft}\left(\text{Counterclockwise}\right)$.

Column shear for member EI, FJ, GK, and HL:

Determine the shear at the end I in the column member EI using the relation.

$S_{IE}=\frac{M_{IE}}{\frac{L_2}{2}}$

Substitute $53\text{k-ft}$ for $M_{IE}$ and 16 ft for $L_2$.

$\begin{array}{c}{S}_{IE}=\frac{53}{\frac{16}{2}}\\ =6.62\text{k}(\to )\end{array}$

The shear at the column member IE must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint I.

Determine the shear at the end of the column E using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{IE}+S_{EI}=0\end{array}$

Substitute 6.62 k for $S_{IE}$.

$\begin{array}{l}6.62+S_{EI}=0\\ S_{EI}=-6.62\text{k}\\ S_{EI}=6.62\text{k}(\leftarrow )\end{array}$

Determine the shear at the end J in the column member FJ using the relation.

$S_{JF}=\frac{M_{JF}}{\frac{L_2}{2}}$

Substitute $37.1\text{k-ft}$ for $M_{EH}$ and 16 ft for $L_2$.

$\begin{array}{c}{S}_{JF}=\frac{37.1}{\frac{16}{2}}\\ =4.64\text{k}(\to )\end{array}$

The shear at the column member JF must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint J.

Determine the shear at the end of the column F using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{JF}+S_{FJ}=0\end{array}$

Substitute 4.64 k for $S_{JF}$.

$\begin{array}{l}4.64+S_{FJ}=0\\ S_{FJ}=-4.64\text{k}\\ S_{FJ}=4.64\text{k}(\leftarrow )\end{array}$

Determine the shear at the end K in the column member GK using the relation.

$S_{KG}=\frac{M_{KG}}{\frac{L_1}{2}}$

Substitute $37.1\text{k-ft}$ for $M_{KG}$ and 16 ft for $L_2$.

$\begin{array}{c}{S}_{KG}=\frac{37.1}{\frac{16}{2}}\\ =4.64\text{k}(\to )\end{array}$

The shear at the column member KG must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint K.

Determine the shear at the end of the column G using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{KG}+S_{GK}=0\end{array}$

Substitute 4.64 k for $S_{KG}$.

$\begin{array}{l}4.64+S_{GK}=0\\ S_{GK}=-4.64\text{k}\\ S_{GK}=4.64\text{k}(\leftarrow )\end{array}$

Determine the shear at the end L in the column member HL using the relation.

$S_{LH}=\frac{M_{LH}}{\frac{L_1}{2}}$

Substitute $53\text{k-ft}$ for $M_{LH}$ and 16 ft for $L_2$.

$\begin{array}{c}{S}_{LH}=\frac{53}{\frac{16}{2}}\\ =6.62\text{k}(\to )\end{array}$

The shear at the column member LH must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint L.

Determine the shear at the end of the column H using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{LH}+S_{HL}=0\end{array}$

Substitute 6.62 k for $S_{LH}$.

$\begin{array}{l}6.62+S_{HL}=0\\ S_{HL}=-6.62\text{k}\\ S_{HL}=6.62\text{k}(\leftarrow )\end{array}$

Column moment for member AE, BF, CG, and DH:

Determine the moment at the column member AE using moment equilibrium of joints.

Apply the moment equilibrium of joints at E.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{EA}-M_{EF}+M_{EI}=0\end{array}$

Substitute $84.75\text{k-ft}$ for $M_{EF}$ and $53\text{k-ft}$ for $M_{EI}$.

$\begin{array}{l}{M}_{EA}-84.75+53=0\\ M_{EA}=31.75\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member AE is $M_{AE}=M_{EA}=31.75\text{k-ft}\left(\text{Counterclockwise}\right)$.

Determine the moment at the column member BF.

Apply the moment equilibrium of joints at F.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{FB}-M_{FE}-M_{FG}+M_{FJ}=0\end{array}$

Substitute $84.75\text{k-ft}$ for $M_{FE}$, $70.6\text{k-ft}$ for $M_{FG}$, and $37.1\text{k-ft}$ for $M_{FJ}$.

$\begin{array}{l}{M}_{FB}-84.75-70.6+37.1=0\\ M_{FB}=118.25\text{k-ft}\left(\text{Counterlockwise}\right)\end{array}$

The moment at the column member BF is $M_{FB}=M_{BF}=118.25\text{k-ft}\left(\text{Counterlockwise}\right)$.

Determine the moment at the column member CG using moment equilibrium of joints.

Apply the moment equilibrium of joints at C.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{GC}-M_{GF}-M_{GH}+M_{GK}=0\end{array}$

Substitute $70.6\text{k-ft}$ for $M_{GF}$, $84.75\text{k-ft}$ for $M_{GH}$, and $37.1\text{k-ft}$ for $M_{GK}$.

$\begin{array}{l}{M}_{GC}-70.6-84.75+37.1=0\\ M_{GC}=118.25\text{k-ft}\left(\text{Counterlockwise}\right)\end{array}$

The moment at the column member CG is $M_{CG}=M_{GC}=118.25\text{k-ft}\left(\text{Counterlockwise}\right)$.

Determine the moment at the column member DH using moment equilibrium of joints.

Apply the moment equilibrium of joints at H.

$\begin{array}{l}{\displaystyle \sum M=0}\\ M_{HD}-M_{HG}+M_{HL}=0\end{array}$

Substitute $84.75\text{k-ft}$ for $M_{HG}$ and $53\text{k-ft}$ for $M_{HL}$.

$\begin{array}{l}{M}_{HD}-84.75+53=0\\ M_{HD}=31.75\text{k-ft}\left(\text{Counterclockwise}\right)\end{array}$

The moment at the column member DH is $M_{DH}=M_{HD}=31.75\text{k-ft}\left(\text{Counterclockwise}\right)$.

Column shear for member AE, BF, CG, and DH:

Determine the shear at the end E in the column member AE using the relation.

$S_{EA}=\frac{M_{EA}}{\frac{L_3}{2}}$

Substitute $31.75\text{k-ft}$ for $M_{EA}$ and 16 ft for $L_3$.

$\begin{array}{c}{S}_{EA}=\frac{31.75}{\frac{16}{2}}\\ =3.97\text{k}(\to )\end{array}$

The shear at the column member EA must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint E.

Determine the shear at the lower end of the column A using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{EA}+S_{AE}=0\end{array}$

Substitute 3.97 k for $S_{EA}$.

$\begin{array}{l}3.97+S_{AE}=0\\ S_{AE}=-3.97\text{k}\\ S_{AE}=3.97\text{k}(\leftarrow )\end{array}$

Determine the shear at the end F in the column member BF using the relation.

$S_{FB}=\frac{M_{FB}}{\frac{L_2}{2}}$

Substitute $118.25\text{k-ft}$ for $M_{EB}$ and 16 ft for $L_3$.

$\begin{array}{c}{S}_{FB}=\frac{118.25}{\frac{16}{2}}\\ =14.78\text{k}(\to )\end{array}$

The shear at the column memer FB must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint F.

Determine the shear at the lower end of the column B using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{FB}+S_{BF}=0\end{array}$

Substitute 14.78 k for $S_{EB}$.

$\begin{array}{l}14.78+S_{BF}=0\\ S_{BF}=-14.78\text{k}\\ S_{BF}=14.78\text{k}(\leftarrow )\end{array}$

Determine the shear at the end G in the column member CG using the relation.

$S_{GC}=\frac{M_{GC}}{\frac{L_3}{2}}$

Substitute $118.25\text{k-ft}$ for $M_{GC}$ and 16 ft for $L_3$.

$\begin{array}{c}{S}_{GC}=\frac{118.25}{\frac{16}{2}}\\ =14.78\text{k}(\to )\end{array}$

The shear at the column member GC must act towards right, so that it can produce counterclockwise moment to balance the clockwise moment at joint G.

Determine the shear at the lower end of the column C using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{GC}+S_{CG}=0\end{array}$

Substitute 14.78 k for $S_{GC}$.

$\begin{array}{l}14.78+S_{CG}=0\\ S_{CG}=-14.78\text{k}\\ S_{CG}=14.78\text{k}(\leftarrow )\end{array}$

Determine the shear at the end H in the column member DH using the relation.

$S_{HD}=\frac{M_{HD}}{\frac{L_3}{2}}$

Substitute $31.75\text{k-ft}$ for $M_{HD}$ and 6 m for $L_3$.

$\begin{array}{c}{S}_{HD}=\frac{31.75}{\frac{16}{2}}\\ =3.97\text{k}(\to )\end{array}$

The shear at the column member HD must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint H.

Determine the shear at the lower end of the column A using equilibrium conditions.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ S_{HD}+S_{DH}=0\end{array}$

Substitute 3.97 k for $S_{HD}$.

$\begin{array}{l}3.97+S_{DH}=0\\ S_{DH}=-3.97\text{k}\\ S_{DH}=3.97\text{k}(\leftarrow )\end{array}$

Draw the free body diagram of frame with the column moments and shears for the portion EIJ as in Figure (9).

Girder axial forces:

Girder MN.

Determine the girder end action at the upper left end joint M using the equilibrium condition.

Apply equilibrium condition at left end joint M.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{MN}-S_{MJ}+H_M=0\end{array}$

Substitute 3.75 k for $S_{MJ}$ and 7.5 k for $H_M$.

$\begin{array}{l}{Q}_{IJ}-3.75+7.5=0\\ Q_{IJ}=-3.75\text{k}\\ Q_{IJ}=3.75\text{k}(\leftarrow )\end{array}$

The girder end action at joint M in the girder MN is $Q_{MN}=3.75\text{k}(\to )$.

Determine the girder end action at the upper right end joint H using the equilibrium condition.

Apply equilibrium condition at end joint M.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{MN}+Q_{NM}=0\end{array}$

Substitute 3.75 k for $Q_{MN}$.

$\begin{array}{l}3.75+Q_{MN}=0\\ Q_{MN}=-3.75\text{k}\\ Q_{MN}=3.75\text{k}(\leftarrow )\end{array}$

Girder IJ.

Determine the girder end action at the upper left end joint I using the equilibrium condition.

Apply equilibrium condition at left end joint I.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{IJ}-S_{IE}+H_I=0\end{array}$

Substitute 6.62 k for $S_{IE}$ and 15 k for $H_I$.

$\begin{array}{l}{Q}_{IJ}-6.62+15=0\\ Q_{IJ}=-8.38\text{k}\\ Q_{IJ}=8.38\text{k}(\leftarrow )\end{array}$

The girder end action at joint I in the girder IJ is $Q_{IJ}=8.38\text{k}(\to )$.

Determine the girder end action at the upper right end joint H using the equilibrium condition.

Apply equilibrium condition at end joint J.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{IJ}+Q_{JI}=0\end{array}$

Substitute 8.38 k for $Q_{IJ}$.

$\begin{array}{l}8.38+Q_{JI}=0\\ Q_{JI}=-8.38\text{k}\\ Q_{JI}=8.38\text{k}(\leftarrow )\end{array}$

Girder JK.

Determine the girder end action at the left end joint J for the girder JK using the relation.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ -Q_{JI}+Q_{JK}+S_{JF}-S_{JM}=0\end{array}$

Substitute 8.38 k for $Q_{JI}$, 4.64 k for $S_{JF}$, and 3.75 k for $S_{JM}$.

$\begin{array}{l}-8.38+Q_{JK}+4.64-3.75=0\\ Q_{JK}=7.49k(\to )\end{array}$

Determine the girder end action at the right end joint K.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{JK}+Q_{KJ}=0\end{array}$

Substitute 7.49 k for $Q_{JK}$.

$\begin{array}{l}7.49+Q_{KJ}=0\\ Q_{KJ}=7.49\text{k}\\ Q_{KJ}=7.49\text{k}(\leftarrow )\end{array}$

Girder KL.

Determine the girder end action at the left end joint K for the girder KL using the relation.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ -Q_{KJ}+Q_{KL}+S_{KG}-S_{KN}=0\end{array}$

Substitute 7.49 k for $Q_{KJ}$, 4.64 k for $S_{KG}$, and 3.75 k for $S_{KN}$.

$\begin{array}{l}-7.49+Q_{KL}+4.64-3.75=0\\ Q_{KL}=6.62\text{k}(\to )\end{array}$

Determine the girder end action at the right end joint L.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{KL}+Q_{LK}=0\end{array}$

Substitute 6.62 k for $Q_{KL}$.

$\begin{array}{l}6.62+Q_{LK}=0\\ Q_{LK}=-6.62\text{k}\\ Q_{LK}=6.62\text{k}(\leftarrow )\end{array}$

Girder EF.

Apply equilibrium condition at left end joint E.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ -Q_{EF}-S_{EA}+S_{EI}+H_E=0\end{array}$

Substitute 3.97 k for $S_{EA}$, 6.62 k for $S_{EI}$, and 15 k for $H_E$.

$\begin{array}{l}-Q_{EF}-3.97+6.62+15=0\\ Q_{EF}=17.65\text{k}(\to )\end{array}$

The girder end action at joint E in the girder EF is $Q_{EF}=17.65\text{k}(\to )$.

Determine the girder end action at the right end joint F using the equilibrium condition.

Apply equilibrium condition at left end joint F.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{EF}+Q_{FE}=0\end{array}$

Substitute 17.65 k for $Q_{EF}$.

$\begin{array}{l}17.65+Q_{FE}=0\\ Q_{FE}=-17.65\text{k}\\ Q_{FE}=17.65\text{k}(\leftarrow )\end{array}$

Determine the girder end action at the left end joint F for the girder FG using equilibrium condition.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{FG}-Q_{FE}+S_{FB}-S_{FJ}=0\end{array}$

Substitute 17.65 k for $Q_{FE}$, 14.78 k for $S_{FB}$, and 4.64 k for $S_{FJ}$.

$\begin{array}{l}{Q}_{FG}-17.65+14.78-4.64=0\\ Q_{FG}=7.51\text{k}(\to )\end{array}$

Determine the girder end action at the right end joint G.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{FG}+Q_{GF}=0\end{array}$

Substitute 7.51 k for $Q_{FG}$.

$\begin{array}{l}7.51+Q_{GF}=0\\ Q_{GF}=-7.51\text{k}\\ Q_{GF}=7.51\text{k}(\leftarrow )\end{array}$

Determine the girder end action at the left end joint G for the girder GH using equilibrium condition.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{GH}-Q_{GF}+S_{GC}-S_{GK}=0\end{array}$

Substitute 7.51 k for $Q_{GF}$, 14.78 k for $S_{GC}$, and 4.64 k for $S_{GK}$.

$\begin{array}{l}{Q}_{GH}-7.51+14.78-4.64=0\\ Q_{GH}=2.63\text{k}(\to )\end{array}$

Determine the girder end action at the right end joint H.

$\begin{array}{l}{\displaystyle \sum F_X}=0\\ Q_{GH}+Q_{HG}=0\end{array}$

Substitute 2.63 k for $Q_{GH}$.

$\begin{array}{l}2.63+Q_{HG}=0\\ Q_{HG}=-2.63\text{k}\\ Q_{HG}=2.63\text{k}(\leftarrow )\end{array}$

Draw the freebody diagram of the member end forces and moments as in Figure (10).

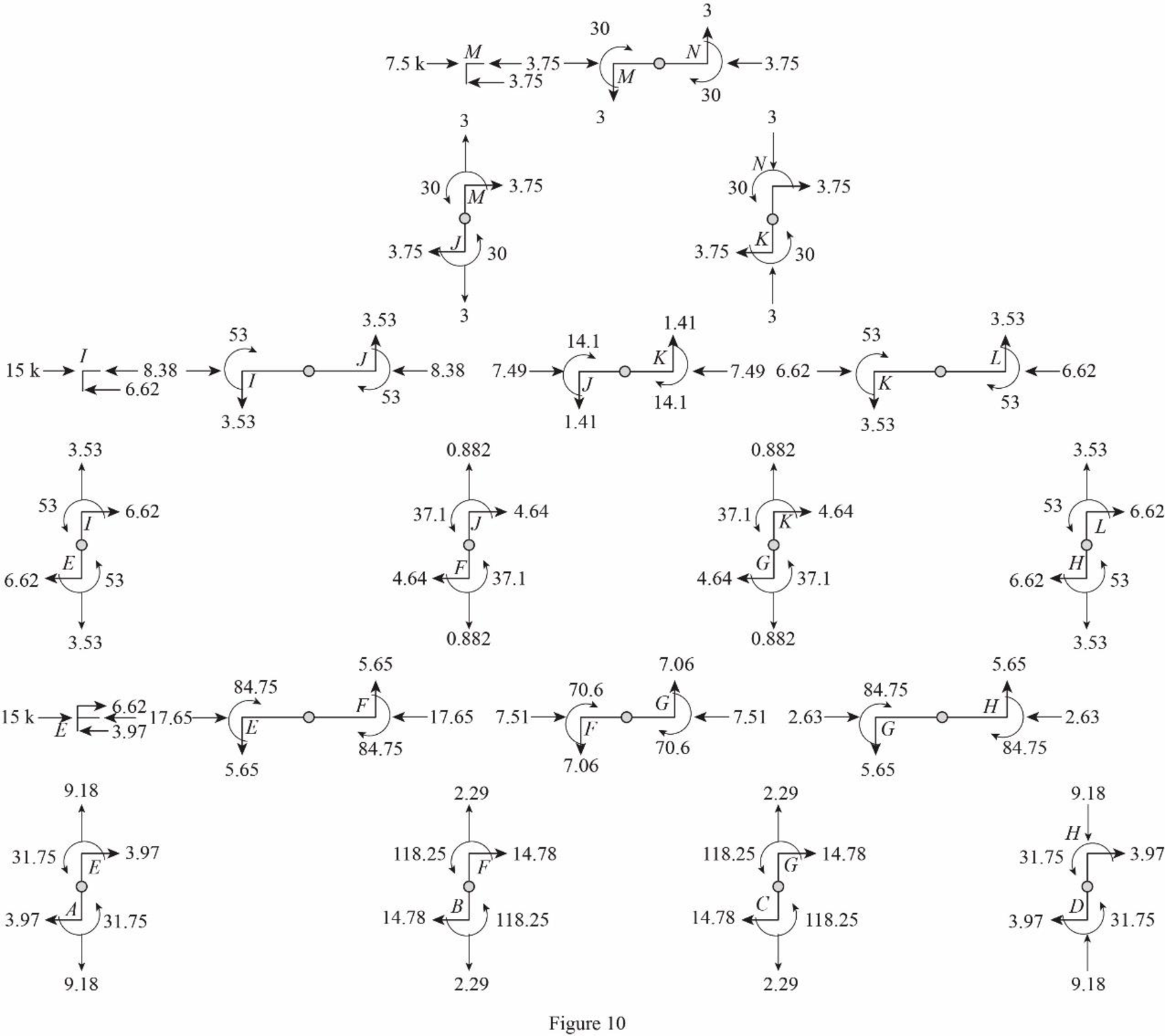
Draw the freebody diagram of the frame with support reactions and moment as in Figure (11).