MATH IN OUR WORLD:ALEKS>CUSTOM<
4th Edition
ISBN: 9781260499544
Author: sobecki
Publisher: MCG CUSTOM
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 12, Problem 1RE
Use this information for Exercises 1–4: the preference ballots for an election for the best speaker in a contest are shown. There are three candidates: Peterson (P), Quintana (Q), and Ross (R).
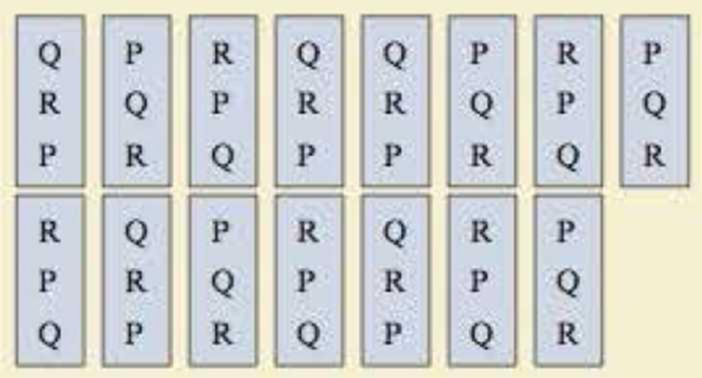
1. Construct a preference table for the results of the election.
Expert Solution & Answer
To determine
To construct: The preference table for the results in the election.
Answer to Problem 1RE
The preference table for the results in the election are listed below.
| Number of votes | 5 | 5 | 5 |
| First choice | Q | P | R |
| Second choice | R | Q | P |
| Third choice | P | R | Q |
Explanation of Solution
Given:
The three candidates are Peterson (P), Quintana (Q) and Ross (R).
The preference table of the best speaker in a contest for the election are listed below.
| Q | P | R | Q | Q | P | R | P | R | Q | P | R | Q | R | P |
| R | Q | P | R | R | Q | P | Q | P | R | Q | P | R | P | Q |
| P | R | Q | P | P | R | Q | R | Q | P | R | Q | P | Q | R |
Calculation:
The choices are Peterson (P), Quintana (Q) and Ross (R).
From the ballot preference table, it is noticed that the candidate order QRP occurs 5 times, the candidate order PQR occurs 5 times and the candidate order RPQ occurs 5 times.
That is, the orders of QRP, PQR and RPQ is 5, 5 and 5.
Therefore, the preference table of the results in the election are listed below.
| Number of votes | 5 | 5 | 5 |
| First choice | Q | P | R |
| Second choice | R | Q | P |
| Third choice | P | R | Q |
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Shading a Venn diagram with 3 sets: Unions, intersections, and...
The Venn diagram shows sets A, B, C, and the universal set U.
Shade (CUA)' n B on the Venn diagram.
U
Explanation
Check
A-
B
Q Search
田
3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain
Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full
with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain
Dew flavors are next to each other?
3.2.1
Business
Chapter 12 Solutions
MATH IN OUR WORLD:ALEKS>CUSTOM<
Ch. 12.1 - The Student Activities Committee at Camden College...Ch. 12.1 - An election was held for the chairperson of the...Ch. 12.1 - Prob. 3TTOCh. 12.1 - Prob. 4TTOCh. 12.1 - Prob. 1ECh. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Explain the head-to head comparison criterion.Ch. 12.1 - 5. What is a fairness criterion for an election?
Ch. 12.1 - Prob. 6E
Ch. 12.1 - Prob. 7ECh. 12.1 - Prob. 8ECh. 12.1 - Prob. 9ECh. 12.1 - Prob. 10ECh. 12.1 - Prob. 11ECh. 12.1 - Prob. 12ECh. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Prob. 15ECh. 12.1 - For Exercises 15–18, rewrite the preference table...Ch. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - Using the election results given in Exercise 9,...Ch. 12.1 - 20. Using the election results given in Exercise...Ch. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - Using the Internet as a resource, look up the...Ch. 12.1 - Suppose that an election has seven candidates, and...Ch. 12.1 - Prob. 25ECh. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - Prob. 29ECh. 12.1 - Prob. 30ECh. 12.1 - Prob. 31ECh. 12.1 - Prob. 32ECh. 12.2 - Prob. 1TTOCh. 12.2 - Prob. 2TTOCh. 12.2 - Prob. 3TTOCh. 12.2 - If the one voter who listed softball last in the...Ch. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Can a candidate that gets the least first-place...Ch. 12.2 - A gaming club holds a vote to decide what type of...Ch. 12.2 - The McKees Point Yacht Club Board of Directors...Ch. 12.2 - Prob. 9ECh. 12.2 - A local police union is holding an election for a...Ch. 12.2 - Students at a college were asked to rank three...Ch. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Does the election in Exercise 12 violate the...Ch. 12.2 - An English department is voting for a new...Ch. 12.2 - The Association of Self-Employed Working Persons...Ch. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Suppose that all 4 voters from the last column of...Ch. 12.2 - Suppose that 2 of the 4 voters from the second...Ch. 12.2 - If 2 of the voters from column 1 in Exercise 21...Ch. 12.2 - If the 3 voters in column 4 in Exercise 22 change...Ch. 12.2 - Construct a preference table for an election...Ch. 12.2 - Construct a preference table for an election...Ch. 12.2 - Construct a preference table for an election so...Ch. 12.2 - If the candidates on a preference ballot are...Ch. 12.2 - If the candidates on a preference ballot are...Ch. 12.2 - In an election with four candidates, how many...Ch. 12.2 - Based on your answers to Exercise 32, explain why...Ch. 12.2 - One way to avoid the issue described in Exercises...Ch. 12.2 - Lets talk about a modified Borda count method....Ch. 12.3 - Prob. 1TTOCh. 12.3 - Prob. 2TTOCh. 12.3 - Does the election in Try This One 2 violate the...Ch. 12.3 - Prob. 4TTOCh. 12.3 - Explain how to determine the winner of an election...Ch. 12.3 - Prob. 2ECh. 12.3 - Describe Arrows impossibility theorem. How is it...Ch. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Which of the five voting methods we studied do you...Ch. 12.3 - If all of the voters in an approval voting...Ch. 12.3 - Fill in the table below, which summarizes our five...Ch. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - The McKees Point Yacht Club Board of Directors...Ch. 12.3 - The students in Dr. Lees math class are asked to...Ch. 12.3 - If Professor Donovan was unable to serve as...Ch. 12.3 - If the travel company from Exercise 14 loses its...Ch. 12.3 - If the West Oak Golf Club is unavailable and the...Ch. 12.3 - If a room for Dr. Lees final exam was not...Ch. 12.3 - A sports committee of students needs to choose a...Ch. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Construct a preference table so that one candidate...Ch. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Prob. 33ECh. 12.3 - Evaluate each voting method we studied if there...Ch. 12.3 - Suppose that in an election for city council,...Ch. 12.3 - Prob. 36ECh. 12.3 - Devise a method for breaking ties when using...Ch. 12.3 - Prob. 38ECh. 12.4 - Prob. 1TTOCh. 12.4 - Prob. 2TTOCh. 12.4 - Prob. 3TTOCh. 12.4 - Prob. 4TTOCh. 12.4 - Prob. 5TTOCh. 12.4 - Assign the 30 seats from Try This One 5 using...Ch. 12.4 - Prob. 7TTOCh. 12.4 - Prob. 8TTOCh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Describe how to find the upper and lower quotas...Ch. 12.4 - Prob. 5ECh. 12.4 - Prob. 6ECh. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - In Exercises 912, find the standard divisor for...Ch. 12.4 - Prob. 12ECh. 12.4 - Prob. 13ECh. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - For Exercises 2628 find: (a)The standard divisor....Ch. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 37ECh. 12.4 - Prob. 38ECh. 12.4 - Prob. 39ECh. 12.4 - Prob. 40ECh. 12.4 - Prob. 41ECh. 12.4 - Prob. 42ECh. 12.4 - Prob. 43ECh. 12.5 - Prob. 1TTOCh. 12.5 - Try This One 2
A county with three districts has...Ch. 12.5 - Prob. 3TTOCh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - What is the quota rule? Which apportionment...Ch. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - The table shows the enrollment at two campuses of...Ch. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Write an essay explaining why many people feel...Ch. 12.5 - 18. Which do you think is more serious: violating...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Use this information for Exercises 917: a large...Ch. 12 - Prob. 16RECh. 12 - Use this information for Exercises 917: a large...Ch. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - A community college bought 15 laptop computers to...Ch. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Repeat exercise 30 using the Huntington-Hill...Ch. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - Prob. 40RECh. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 1CTCh. 12 - Prob. 2CTCh. 12 - Prob. 3CTCh. 12 - Prob. 4CTCh. 12 - Prob. 5CTCh. 12 - Prob. 6CTCh. 12 - Prob. 7CTCh. 12 - Prob. 8CTCh. 12 - Use this information for Exercises 512: a small...Ch. 12 - Prob. 10CTCh. 12 - Prob. 11CTCh. 12 - Prob. 12CTCh. 12 - Prob. 13CTCh. 12 - An airline offers nonstop flights from Fort...Ch. 12 - Prob. 15CTCh. 12 - Repeat Problem 14 using Websters method.Ch. 12 - Repeat Problem 14 using the Huntington-Hill...Ch. 12 - Prob. 18CTCh. 12 - Prob. 19CTCh. 12 - Prob. 20CTCh. 12 - Prob. 21CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Please explain how come of X2(n).arrow_forwardNo chatgpt pls will upvotearrow_forwardFind all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forward
- https://www.hawkeslearning.com/Statistics/dbs2/datasets.htmlarrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forward
- Let A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective. why?(b) Determine if f is surjective. why?(c) Based upon (a) and (b), is f bijective? why?arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective.(b) Determine if f is surjective. (c) Based upon (a) and (b), is f bijective?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
12. Searching and Sorting; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=6LOwPhPDwVc;License: Standard YouTube License, CC-BY
Algorithms and Data Structures - Full Course for Beginners from Treehouse; Author: freeCodeCamp.org;https://www.youtube.com/watch?v=8hly31xKli0;License: Standard Youtube License