MATH IN OUR WORLD (LOOSELEAF)-W/ACCESS
3rd Edition
ISBN: 9781259969690
Author: sobecki
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 12, Problem 1RE
Use this information for Exercises 1–4: the preference ballots for an election for the best speaker in a contest are shown. There are three candidates: Peterson (P), Quintana (Q), and Ross (R).
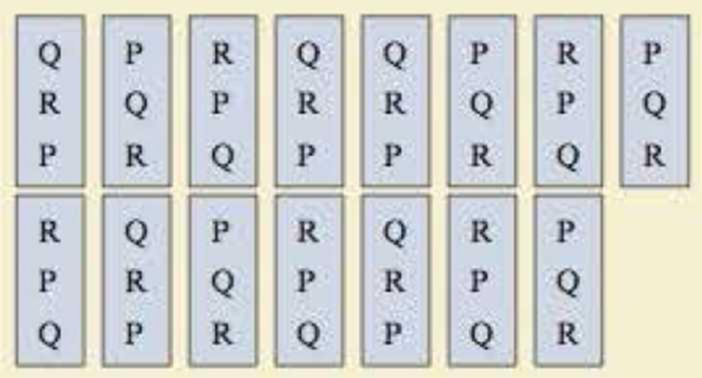
1. Construct a preference table for the results of the election.
Expert Solution & Answer
To determine
To construct: The preference table for the results in the election.
Answer to Problem 1RE
The preference table for the results in the election are listed below.
| Number of votes | 5 | 5 | 5 |
| First choice | Q | P | R |
| Second choice | R | Q | P |
| Third choice | P | R | Q |
Explanation of Solution
Given:
The three candidates are Peterson (P), Quintana (Q) and Ross (R).
The preference table of the best speaker in a contest for the election are listed below.
| Q | P | R | Q | Q | P | R | P | R | Q | P | R | Q | R | P |
| R | Q | P | R | R | Q | P | Q | P | R | Q | P | R | P | Q |
| P | R | Q | P | P | R | Q | R | Q | P | R | Q | P | Q | R |
Calculation:
The choices are Peterson (P), Quintana (Q) and Ross (R).
From the ballot preference table, it is noticed that the candidate order QRP occurs 5 times, the candidate order PQR occurs 5 times and the candidate order RPQ occurs 5 times.
That is, the orders of QRP, PQR and RPQ is 5, 5 and 5.
Therefore, the preference table of the results in the election are listed below.
| Number of votes | 5 | 5 | 5 |
| First choice | Q | P | R |
| Second choice | R | Q | P |
| Third choice | P | R | Q |
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
1 2
21. For the matrix A
=
3 4
find AT (the transpose of A).
22. Determine whether the vector
@
1
3
2
is perpendicular to
-6
3
2
23. If v1
=
(2)
3
and v2 =
compute V1 V2 (dot product).
.
7. Find the eigenvalues of the matrix
(69)
8. Determine whether the vector
(£)
23
is in the span of the vectors
-0-0
and
2
2
1. Solve for x:
2. Simplify:
2x+5=15.
(x+3)² − (x − 2)².
-
b
3. If a = 3 and 6 = 4, find (a + b)² − (a² + b²).
4. Solve for x in 3x² - 12 = 0.
-
Chapter 12 Solutions
MATH IN OUR WORLD (LOOSELEAF)-W/ACCESS
Ch. 12.1 - The Student Activities Committee at Camden College...Ch. 12.1 - An election was held for the chairperson of the...Ch. 12.1 - Prob. 3TTOCh. 12.1 - Prob. 4TTOCh. 12.1 - Prob. 1ECh. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Explain the head-to head comparison criterion.Ch. 12.1 - 5. What is a fairness criterion for an election?
Ch. 12.1 - Prob. 6E
Ch. 12.1 - Prob. 7ECh. 12.1 - Prob. 8ECh. 12.1 - Prob. 9ECh. 12.1 - Prob. 10ECh. 12.1 - Prob. 11ECh. 12.1 - Prob. 12ECh. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Prob. 15ECh. 12.1 - For Exercises 15–18, rewrite the preference table...Ch. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - Using the election results given in Exercise 9,...Ch. 12.1 - 20. Using the election results given in Exercise...Ch. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - Using the Internet as a resource, look up the...Ch. 12.1 - Suppose that an election has seven candidates, and...Ch. 12.1 - Prob. 25ECh. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - Prob. 29ECh. 12.1 - Prob. 30ECh. 12.1 - Prob. 31ECh. 12.1 - Prob. 32ECh. 12.2 - Prob. 1TTOCh. 12.2 - Prob. 2TTOCh. 12.2 - Prob. 3TTOCh. 12.2 - If the one voter who listed softball last in the...Ch. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Can a candidate that gets the least first-place...Ch. 12.2 - A gaming club holds a vote to decide what type of...Ch. 12.2 - The McKees Point Yacht Club Board of Directors...Ch. 12.2 - Prob. 9ECh. 12.2 - A local police union is holding an election for a...Ch. 12.2 - Students at a college were asked to rank three...Ch. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Does the election in Exercise 12 violate the...Ch. 12.2 - An English department is voting for a new...Ch. 12.2 - The Association of Self-Employed Working Persons...Ch. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Suppose that all 4 voters from the last column of...Ch. 12.2 - Suppose that 2 of the 4 voters from the second...Ch. 12.2 - If 2 of the voters from column 1 in Exercise 21...Ch. 12.2 - If the 3 voters in column 4 in Exercise 22 change...Ch. 12.2 - Construct a preference table for an election...Ch. 12.2 - Construct a preference table for an election...Ch. 12.2 - Construct a preference table for an election so...Ch. 12.2 - If the candidates on a preference ballot are...Ch. 12.2 - If the candidates on a preference ballot are...Ch. 12.2 - In an election with four candidates, how many...Ch. 12.2 - Based on your answers to Exercise 32, explain why...Ch. 12.2 - One way to avoid the issue described in Exercises...Ch. 12.2 - Lets talk about a modified Borda count method....Ch. 12.3 - Prob. 1TTOCh. 12.3 - Prob. 2TTOCh. 12.3 - Does the election in Try This One 2 violate the...Ch. 12.3 - Prob. 4TTOCh. 12.3 - Explain how to determine the winner of an election...Ch. 12.3 - Prob. 2ECh. 12.3 - Describe Arrows impossibility theorem. How is it...Ch. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Which of the five voting methods we studied do you...Ch. 12.3 - If all of the voters in an approval voting...Ch. 12.3 - Fill in the table below, which summarizes our five...Ch. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - The McKees Point Yacht Club Board of Directors...Ch. 12.3 - The students in Dr. Lees math class are asked to...Ch. 12.3 - If Professor Donovan was unable to serve as...Ch. 12.3 - If the travel company from Exercise 14 loses its...Ch. 12.3 - If the West Oak Golf Club is unavailable and the...Ch. 12.3 - If a room for Dr. Lees final exam was not...Ch. 12.3 - A sports committee of students needs to choose a...Ch. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Construct a preference table so that one candidate...Ch. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Prob. 33ECh. 12.3 - Evaluate each voting method we studied if there...Ch. 12.3 - Suppose that in an election for city council,...Ch. 12.3 - Prob. 36ECh. 12.3 - Devise a method for breaking ties when using...Ch. 12.3 - Prob. 38ECh. 12.4 - Prob. 1TTOCh. 12.4 - Prob. 2TTOCh. 12.4 - Prob. 3TTOCh. 12.4 - Prob. 4TTOCh. 12.4 - Prob. 5TTOCh. 12.4 - Assign the 30 seats from Try This One 5 using...Ch. 12.4 - Prob. 7TTOCh. 12.4 - Prob. 8TTOCh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Describe how to find the upper and lower quotas...Ch. 12.4 - Prob. 5ECh. 12.4 - Prob. 6ECh. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - In Exercises 912, find the standard divisor for...Ch. 12.4 - Prob. 12ECh. 12.4 - Prob. 13ECh. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - For Exercises 2628 find: (a)The standard divisor....Ch. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 37ECh. 12.4 - Prob. 38ECh. 12.4 - Prob. 39ECh. 12.4 - Prob. 40ECh. 12.4 - Prob. 41ECh. 12.4 - Prob. 42ECh. 12.4 - Prob. 43ECh. 12.5 - Prob. 1TTOCh. 12.5 - Try This One 2
A county with three districts has...Ch. 12.5 - Prob. 3TTOCh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - What is the quota rule? Which apportionment...Ch. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - The table shows the enrollment at two campuses of...Ch. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Write an essay explaining why many people feel...Ch. 12.5 - 18. Which do you think is more serious: violating...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Use this information for Exercises 917: a large...Ch. 12 - Prob. 16RECh. 12 - Use this information for Exercises 917: a large...Ch. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - A community college bought 15 laptop computers to...Ch. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Repeat exercise 30 using the Huntington-Hill...Ch. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - Prob. 40RECh. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 1CTCh. 12 - Prob. 2CTCh. 12 - Prob. 3CTCh. 12 - Prob. 4CTCh. 12 - Prob. 5CTCh. 12 - Prob. 6CTCh. 12 - Prob. 7CTCh. 12 - Prob. 8CTCh. 12 - Use this information for Exercises 512: a small...Ch. 12 - Prob. 10CTCh. 12 - Prob. 11CTCh. 12 - Prob. 12CTCh. 12 - Prob. 13CTCh. 12 - An airline offers nonstop flights from Fort...Ch. 12 - Prob. 15CTCh. 12 - Repeat Problem 14 using Websters method.Ch. 12 - Repeat Problem 14 using the Huntington-Hill...Ch. 12 - Prob. 18CTCh. 12 - Prob. 19CTCh. 12 - Prob. 20CTCh. 12 - Prob. 21CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 5. Find the derivative of f(x) = 6. Evaluate the integral: 3x3 2x²+x— 5. - [dz. x² dx.arrow_forward5. Find the greatest common divisor (GCD) of 24 and 36. 6. Is 121 a prime number? If not, find its factors.arrow_forward13. If a fair coin is flipped, what is the probability of getting heads? 14. A bag contains 3 red balls and 2 blue balls. If one ball is picked at random, what is the probability of picking a red ball?arrow_forward
- 24. What is the value of ¿4, where i 25. Simplify log2 (8). = −1? 26. If P(x) = x³- 2x² + 5x - 10, find P(2). 27. Solve for x: e2x = 7.arrow_forward9. Solve the differential equation: 10. Find the general solution of dy + y = 0. dy 33 dx 3x².arrow_forward3. Differentiate f(x) = x² sin(x). 4. Evaluate the limit: sin(2x) lim xarrow_forward
- 1. Solve for x in the equation: 2. If A = (1/3 2/) 4 x³-3x²+4=0 find the determinant of A.arrow_forwardListen ANALYZING RELATIONSHIPS Describe the x-values for which (a) f is increasing or decreasing, (b) f(x) > 0 and (c) f(x) <0. y Af -2 1 2 4x a. The function is increasing when and decreasing whenarrow_forwardBy forming the augmented matrix corresponding to this system of equations and usingGaussian elimination, find the values of t and u that imply the system:(i) is inconsistent.(ii) has infinitely many solutions.(iii) has a unique solutiona=2 b=1arrow_forward3/4+1/2=arrow_forwardif a=2 and b=1 1) Calculate 49(B-1)2+7B−1AT+7ATB−1+(AT)2 2)Find a matrix C such that (B − 2C)-1=A 3) Find a non-diagonal matrix E ̸= B such that det(AB) = det(AE)arrow_forward1.2.17. (!) Let G,, be the graph whose vertices are the permutations of (1,..., n}, with two permutations a₁, ..., a,, and b₁, ..., b, adjacent if they differ by interchanging a pair of adjacent entries (G3 shown below). Prove that G,, is connected. 132 123 213 312 321 231arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
12. Searching and Sorting; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=6LOwPhPDwVc;License: Standard YouTube License, CC-BY
Algorithms and Data Structures - Full Course for Beginners from Treehouse; Author: freeCodeCamp.org;https://www.youtube.com/watch?v=8hly31xKli0;License: Standard Youtube License