
In Exercises 1–8, find all the relative and absolute extrema of the given function on the given domain (if supplied) or on the largest possible domain (if no domain is supplied).
To calculate: The exact location of the relative and absolute extrema of the function
Answer to Problem 1RE
Solution:
The exact location of Absolute Minimum are
Explanation of Solution
Given Information:
The provided equation is:
Formula used:
First Derivative Test is, assume that for a critical point
If
If
If
Stationary Points are the points in the interior of the domain where the derivative is zero.
Singular Points are the points in the interior of the domain where the derivative is not defined.
Closed intervals contain end points which are the end points of the functions and the function does not have end points if the interval is open as open intervals do not have any end points.
Calculation:
Consider the provided equation:
Differentiate both sides of the equation with respect to
Now, locate stationary points.
Recall that stationary Points are the points in the interior of the domain where the derivative is zero.
Adding
Multiplying both sides of the equation by
Taking square root of both sides of the equation to get:
The domain of the function is
Now locate singular points.
Since
Next locate end points.
Since
The values of
| 5 | 5 |
The graph increases from
Use the above points to plot a graph
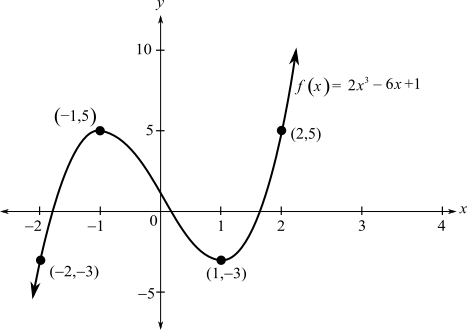
From figure we can see that
| Classification | ||
| Absolute Minimum | ||
| Absolute Minimum | ||
| Relative Maximum |
Therefore, the exact location of Absolute Minimum are
Want to see more full solutions like this?
Chapter 12 Solutions
Finite Mathematics and Applied Calculus (MindTap Course List)
- 2. Find a matrix A with the following qualities a. A is 3 x 3. b. The matrix A is not lower triangular and is not upper triangular. c. At least one value in each row is not a 1, 2,-1, -2, or 0 d. A is invertible.arrow_forwardFind the exact area inside r=2sin(2\theta ) and outside r=\sqrt(3)arrow_forwardA 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forward
- Explain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
