
Concept explainers
Classify each angle as right, acute, or obtuse:

The classification of the provided angle shown below as right, acute or obtuse angle.
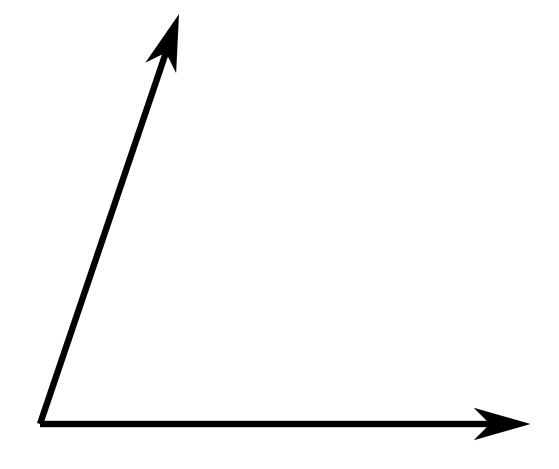
Answer to Problem 1R
Solution:
The angle shown in the provided figure is an acute angle.
Explanation of Solution
Given Information:
An angle as shown in the below figure:

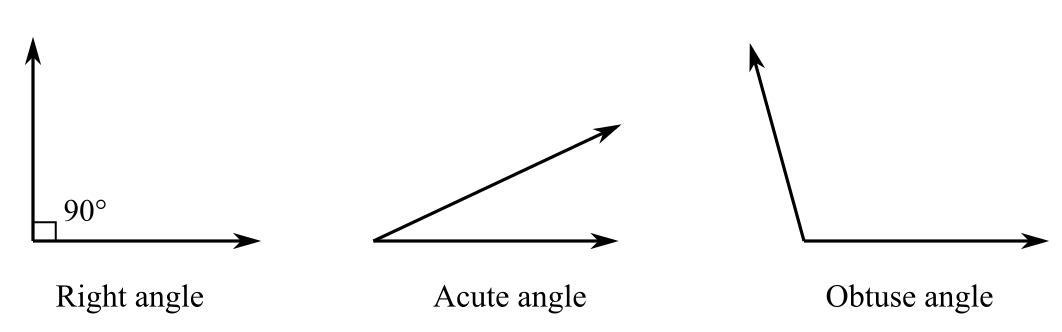
The angles can be classified on the basis of the degree measure.
A right angle is an angle with a measure of
An acute angle is an angle with a measure less than
An obtuse angle is an angle with a measure greater than
All the three types of angles are shown below in the figure:
From the provided figure, it is observed that measure of the angle is less than
Thus, the angle shown in the provided figure is an acute angle.
Want to see more full solutions like this?
Chapter 12 Solutions
Elementary Technical Mathematics
- : +0 1 R2X2 العنوان I need a detailed drawing with explanation L L 2) slots per pole per phase = 3/31 B = 180-60 msl Kd Kol, Sin (Info) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 6 50105 1000 S=1000-950 Loco mem 6. Copper losses: 5kw Rotor input loo kw 0.05 اذا ميريد شرح الكتب فقط look 7) rotov DC ined sove in peaper Pu+965 4 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 111Σm=1 sin() Lake Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. T TH Marrow_forwardい ined sove in beaper Anting. Pu+965 na lake an accident and lands at the bottom of the lake Q2// Find the volume of the region in first octant bounded by the coordinate planes and the plane passing through (1, 0, 0), (0, 2, 0), and (0, 0, 3). Q/Evaluate({ } } 3xze* dydzdx.arrow_forward| Evaluate (3xze** dydzdx. ined sove in peaper +9198 PU+965 Lake Find the volume of th solid bounded above by the Cy 2=6-1 o the sides by the cylinder x+y=9, and below by the xy-planearrow_forward
- ... +① العنوان > पर ined sove in peaper ང་ PU+965 Q2// Draw and Evaluate, or Integrate, the function f(u, v) = (1+u2+v²)3 over the region enclosed by one loop of the lemniscate (u² + v²)² - (u² + v²) = 0. Lake 2 4-2² y 7357 r QI// Evaluate f²² cos(y) dxdydz. 4-y 이arrow_forwardPlease show all steps and write out the answer instead of typing it out, thanksarrow_forwardし ined sove in peaper Anot in PV+96252 √4-x²-y² Q4// Convert √ √ √2x-x2 √√4-x-2_ 21xy² dzdydx to (a) cylindrical coordinates, (b) Spherical coordinates. ln3 (m3)2-x2 Q Draw and Evaluate Lake √x²+ dydarrow_forward
- : +0 1 R2X2 العنوان I need a detailed drawing with explanation L L 2) slots per pole per phase = 3/31 B = 180-60 msl Kd Kol, Sin (Info) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 6 50105 1000 S=1000-950 Loco mem 6. Copper losses: 5kw Rotor input loo kw 0.05 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper PU + 96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 5100 2n=2√²+n Lake Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. T (3n)! 00 //Σn=1 (1+n)!(2+n)!" TH Marrow_forward۳/۱ : +♡ العنوان R2 X2 2) slots per pole per phase = 3/31 B-180-60 msl Kd Kas Sin (1) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس بالفراغ 3) Cos (30) 0.866 レ× 4) Rotating 5) Synchronous speed, 120 x 50 G S=1000-950 50105 1000 looo rem > ined sove in pea Copper losses 5kw Rotor input: 5 0.05 (lookw) bos cid PU+965 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. 7) rotor !!Σn=1 (1-1)" が Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. 5700 Prove that the p-series Σn=11 (p areal constant) converges if, and diverges otherwise. T Τ Lake Marrow_forwardVo)) %TV .. + 1 R2X2 2) slots per pole per phase = 3/31 B-180-60 msl Kol Sin () Isin () Kd تب بس بالفراغ i Cos (30) 0.866 4) Rotating ۳/۱ 5) Synchronous speed; 12 S=1000-950 50 1000 Copper losses: 5kw Rotor input 5 loo kw 0.05 6) I العنوان Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. اذا ميريد شرح الكتب فقط ok 7) rotor ||| DC 11500 30tan¹() 2n=1' m²+1 1:11 > PV + 16°52 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. 7357 //Σm=1 (m²-5n+6) Lake Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. - (3)(5+)) T d sove in peaper =T Marrow_forward
- PROBLEM 1: A 12-lb rod ABC is impacted by a 2-lb object DE as shown. The object embeds into the end of the rod at point C, determine immediately after the impact (a) the angular velocity of the rod ABC, (b) the angular acceleration of the rod ABC, A 2 B Unit: ft (c) the components of the reaction at B. 12 Assume that the object and the rod move as a single body after the impact. Vo = 35 ft/s C E D 6arrow_forwardPlease answer both questions clearly thanksarrow_forwardL ined sove in peaper Anoting PU+965 4 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. +1Σm=1 00 sin Sn Lake 55 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 5700 2n=2√2+n Carrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,



