
Concept explainers
Figure 12-15 shows three situations in which the same horizontal rod is supported by a hinge on a wall at one end and a cord at its other end. Without written calculation, rank the situations according to the magnitudes of (a) the force on the rod from the cord, (b) the vertical force on the rod from the hinge, and (c) the horizontal force on the rod from the hinge, greatest first.
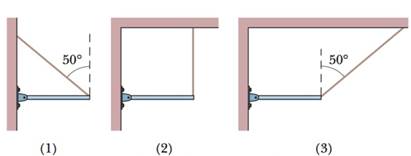
Figure 12-15 Question 1.
To rank:
a) The situations according to the magnitudes of the force on the rod from the cord.
b) The situations according to the magnitudes of the vertical force on the rod from the hinge.
c) The situations according to the magnitudes of the horizontal force on the rod form the hinge.
Answer to Problem 1Q
Solution:
a) Magnitudes of force on the rod from the cord in case (1) and (3) is same and greater than that in case (2).
b) Magnitudes of the vertical force on the rod from the hinge is same for all 3 cases.
c) Magnitudes of the horizontal force on the rod form the hinge is same in cases (1) and (3) and is zero in case (2)
Explanation of Solution
1) Concept:
We can use the concept of balancing of forces and torque at equilibrium to rank the situations according to the magnitude of the forces.
2) Formulae:
At equilibrium,
i.
ii.
3) Given:
i. The figure of rod-cable system.
ii. The angle made by the cord with the vertical direction in case 1 and 3 is 500
4) Calculation:
a) We consider the hinge point as the point of rotation. The torques acting on the rod are due to tension in the string and the weight of the rod. In all the three cases, the rod is in static equilibrium, hence:
The weight of the rod is acting at its centre and is the same in magnitude. Hence the torque equation tells us that torque due to tension, it is same in all the cases.
But the cord is making an angle with the vertical in cases (1) and (3). Hence we understand that the torque due to vertical component of the tension (T cos 50o) is the same. Since it is a component of the total tension, we know that the total tension is greater than the components in cases (1) and (3).Thus, for cases (1) and (3) the tension in the string is same and it will be greater than this in case (2).
b) We consider the hinge point as the point of rotation. In all the three cases, the rod is in static equilibrium. So the torques acting on the rod due to the tension in the string and the weight of the rod are balanced and the forces are also balanced.
Thus the vertical force from the hinge on the rod is same in all the three cases.
c) The forces acting on the rod in the horizontal direction are the force from hinge and the horizontal component of tension in the cord. In cases (1) and (3), the tension in the string is the same. Hence their corresponding horizontal components are also the same.
Thus, the horizontal force on the rod from the hinge is the same in cases (1) and (3). In case (2), there is no horizontal component of tension, hence the horizontal force from the hinge is also zero.
Conclusion:
The rod is in static equilibrium in all three cases. From the balancing conditions for torque and forces, we can determine the magnitudes of the forces acting on the rod.
Want to see more full solutions like this?
Chapter 12 Solutions
Fundamentals Of Physics 11e Student Solutions Manual
Additional Science Textbook Solutions
Human Physiology: An Integrated Approach (8th Edition)
Campbell Biology (11th Edition)
Organic Chemistry
Microbiology: An Introduction
Biology: Life on Earth with Physiology (11th Edition)
College Physics: A Strategic Approach (3rd Edition)
- 20. Two small conducting spheres are placed on top of insulating pads. The 3.7 × 10-10 C sphere is fixed whie the 3.0 × 107 C sphere, initially at rest, is free to move. The mass of each sphere is 0.09 kg. If the spheres are initially 0.10 m apart, how fast will the sphere be moving when they are 1.5 m apart?arrow_forwardpls help on allarrow_forwardpls help on thesearrow_forward
- pls help on all asked questions kindlyarrow_forwardpls help on all asked questions kindlyarrow_forward19. Mount Everest, Earth's highest mountain above sea level, has a peak of 8849 m above sea level. Assume that sea level defines the height of Earth's surface. (re = 6.38 × 106 m, ME = 5.98 × 1024 kg, G = 6.67 × 10 -11 Nm²/kg²) a. Calculate the strength of Earth's gravitational field at a point at the peak of Mount Everest. b. What is the ratio of the strength of Earth's gravitational field at a point 644416m below the surface of the Earth to a point at the top of Mount Everest? C. A tourist watching the sunrise on top of Mount Everest observes a satellite orbiting Earth at an altitude 3580 km above his position. Determine the speed of the satellite.arrow_forward
- pls help on allarrow_forwardpls help on allarrow_forward6. As the distance between two charges decreases, the magnitude of the electric potential energy of the two-charge system: a) Always increases b) Always decreases c) Increases if the charges have the same sign, decreases if they have the opposite signs d) Increases if the charges have the opposite sign, decreases if they have the same sign 7. To analyze the motion of an elastic collision between two charged particles we use conservation of & a) Energy, Velocity b) Momentum, Force c) Mass, Momentum d) Energy, Momentum e) Kinetic Energy, Potential Energyarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





