
Assume
a. List the congruent angles and congruent sides.
b. List all possible ways that the congruence can be symbolized.
(a)
To list:
The congruent angles and congruent sides if
Answer to Problem 1NT
Solution:
The congruent angles are
Explanation of Solution
Definition used:
The triangles are congruent or corresponding parts if they have exactly the same three sides and exactly the same three angles.
Rules for two triangles are congruent:
1. SSS: If three sides of the triangles are equal to the sides of another triangle, then the two triangles are congruent.
2. SAS: If two sides and included angle of one triangle are equal to corresponding sides and angle of another triangle, then the two triangles are congruent.
3. ASA: If two angles and included side of one triangle are equal to corresponding angles and side of another triangle, then the triangles two are congruent.
4. AAS: If two angles and non-included side of one triangle are equal to corresponding angles and side of another triangle, then the two triangles are congruent.
5. HL: If the hypotenuse and one leg of one right-angled triangle are equal to corresponding hypotenuse and leg of another right-angled triangle, then the two triangles are congruent.
Calculation:
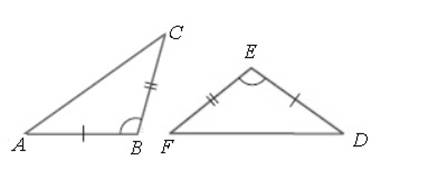
Draw the traingles
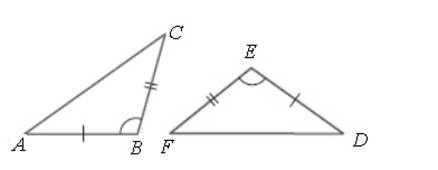
From the above triangle, it is observed that
Here, the two sides and included angle of one triangle are equal to corresponding sides and angle of another triangle.
Check the congruent by finding all the six corresponding parts of the two triangles
Compute the corresponding sides of
Compute the corresponding angles of
Therefore, all the six corresponding parts are congruent.
Hence, the triangles are congruent
Final Statement:
The corresponding parts of the triangles are obtained.
(b)
To list:
All the possible ways to symbolize the congruence.
Explanation of Solution
Calculation:
All the possible ways to symbolize the congruence is as follows.
1.
2.
3.
4.
5.
6.
Want to see more full solutions like this?
Chapter 12 Solutions
A Problem Solving Approach to Mathematics for Elementary School Teachers (12th Edition)
- what would a of a interscribed angle be with an arc of 93 degrees and inside abgles of 111 and 98arrow_forwardFrom a sample of 26 graduate students, the mean number of months of work experience prior to entering an MBA program was 34.67. The national standard deviation is known to be18 months. What is a 90% confidence interval for the population mean? Question content area bottom Part 1 A 9090% confidence interval for the population mean is left bracket nothing comma nothing right bracketenter your response here,enter your response here. (Use ascending order. Round to two decimal places as needed.)arrow_forwardA person leaves home and walks 3 miles west, then 4 miles southwest. How far from home is she? miles In what direction must she walk to head directly home? degrees North of East Question Help: Video Submit Question Jump to Answerarrow_forward
- whats this answer Ginger records her grades for each assignment in science.arrow_forwardConsider the electrical circuit shown in Figure P6-41. It consists of two closed loops. Taking the indicated directions of the currents as positive, obtain the differential equations governing the currents I1 and I2 flowing through the resistor R and inductor L, respectively.arrow_forwardSolve the following initial value problem the initial conditions aw +3. = 12z+18 +9, Əz2 მი w(x, 0)=2x3+3x²+8x ду From (38) auction we obtain follow (x, 0) =i (6x²-6x+2).arrow_forward
- Calculus lll May I please have the semicolon statements in the boxes explained and completed? Thank you so mucharrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forward
- Dalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work. Dear Student If You Face any issue let me know i will solve your all doubt. I will provide solution again in more detail systematic and organized way. I would also like my last 3 questions credited to mearrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work.arrow_forwardQuestion 1 20 pts Test data on the bending strength of construction wood poles of various diameter are presented below assuming the same length. Kip- 1000 lbf. Using the following data with 2nd order Newton polynomial interpolation, we want to determine the strength of the material for x=4.9 in. Which data point will be used as x? After you found x0, enter the value of x-xo in the solution. Answer shall be in one decimal place. Distance (in) Strength (kips) 100 3.6 1.1 5.6 3.6 5.6 200 300 400 500arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning  Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,





