
Concept explainers
Consider the construction of a Koch snowflake starting with a seed triangle having sides of length 81 cm. Let M denote the number of sides, L the length of each side, and P the perimeter of the "snowflake" obtained at the indicated step of the construction. Complete the missing entries in Table 12-1 Q.
Table 12-1
| M | L | P | |
| Start | 3 | 81 cm | 243 cm |
| Step 1 | 12 | 27 cm | 324 cm |
| Step 2 | |||
| Step 3 | |||
| Step 4 | |||
| Step 5 |
To complete:
The given chart.
Answer to Problem 1E
Solution:
The given chart is,
| M | L | P | |
| Start | 3 | ||
| Step 1 | 12 | ||
| Step 2 | 48 | ||
| Step 3 | 192 | ||
| Step 4 | 768 | ||
| Step 5 | 3072 |
Explanation of Solution
Given:
The given chart is,
| M | L | P | |
| Start | 3 | 81 cm | 243 cm |
| Step 1 | 12 | 27 cm | 324 cm |
| Step 2 | |||
| Step 3 | |||
| Step 4 | |||
| Step 5 |
Calculation:
Draw an equilateral triangle with side length of
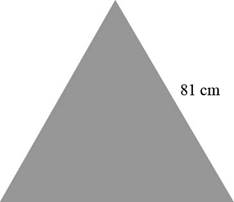
Figure-1
To the middle third of each of the sides of this seed, add an equilateral triangle with sides of length 27 cm. The result is a 12 sided snowflake with perimeter,

Figure-2
To the middle third of each of the 12 sides of snowflake add an equilateral triangle with sides of length one third of the length of the side. The result is a snowflake with 48 sides each side length of 9 cm and the perimeter is,

Figure-3
| M | L | P | |
| Start | 3 | ||
| Step 1 | 12 | ||
| Step 2 | 48 | ||
| Step 3 | 192 | ||
| Step 4 | 768 | ||
| Step 5 | 3072 |
Therefore, the given chart calculations are stated above.
Want to see more full solutions like this?
Chapter 12 Solutions
Excursions in Modern Mathematics (9th Edition)
- Suppose that a particle moves along a straight line with velocity v (t) = 62t, where 0 < t <3 (v(t) in meters per second, t in seconds). Find the displacement d (t) at time t and the displacement up to t = 3. d(t) ds = ["v (s) da = { The displacement up to t = 3 is d(3)- meters.arrow_forwardLet f (x) = x², a 3, and b = = 4. Answer exactly. a. Find the average value fave of f between a and b. fave b. Find a point c where f (c) = fave. Enter only one of the possible values for c. c=arrow_forwardThe following data represent total ventilation measured in liters of air per minute per square meter of body area for two independent (and randomly chosen) samples. Analyze these data using the appropriate non-parametric hypothesis testarrow_forward
- each column represents before & after measurements on the same individual. Analyze with the appropriate non-parametric hypothesis test for a paired design.arrow_forwardShould you be confident in applying your regression equation to estimate the heart rate of a python at 35°C? Why or why not?arrow_forwardGiven your fitted regression line, what would be the residual for snake #5 (10 C)?arrow_forward
- Calculate the 95% confidence interval around your estimate of r using Fisher’s z-transformation. In your final answer, make sure to back-transform to the original units.arrow_forwardCalculate Pearson’s correlation coefficient (r) between temperature and heart rate.arrow_forwardCalculate the least squares regression line and write the equation.arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





