
Concept explainers
(a)
Interpretation: The density of bcc iron when the radius of an iron atom is given to be
Concept introduction: The density of a unit cell is calculated by the formula,
The mass of a unit cell is calculated by the formula,
To determine: The density of bcc iron when the radius of an iron atom is
(a)
Answer to Problem 12.95AP
Solution
The density of bcc iron is
Explanation of Solution
Explanation
The density of bcc iron is calculated by the formula,
The number of atoms in the unit cell is two when iron has the bcc structure.
The
Substitute these values in the formula of mass of the unit cell,
The mass of bcc
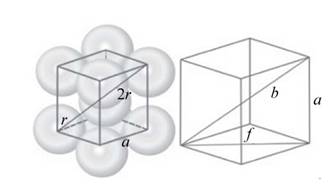
Figure 1
From Figure 1, the relationship between the radius of the iron sphere and the edge length of the unit cell is determined by the formula,
Face diagonal is calculated by the formula,
Body diagonal is calculated by the formula,
Thus, from equations (1) and (2),
The volume of the unit cell
Since,
The volume is calculated by the formula,
The volume of the unit cell in centimeters is,
The density of the unit cell is calculated by the formula,
Substitute the values of mass and that of volume of the unit cell,
Therefore, the density of bcc iron is
(b)
To determine: The density of hexagonal iron given a volume of unit cell is
(b)
Answer to Problem 12.95AP
Solution
The density of hcp iron is
Explanation of Solution
Explanation
The density of the hcp iron is calculated by the formula,
The number of atoms in the unit cell is two when iron has the hcp structure.
The atomic mass of
Substitute these values in the formula of mass of the unit cell,
The mass of hcp
The unit cell volume of hcp iron is given as
The density of the unit cell is calculated by the formula,
Substitute the values of mass and that of volume of the unit cell,
Therefore, the density of hcp iron is
(c)
To determine: The density of a crystal that has
(c)
Answer to Problem 12.95AP
Solution
The density of hcp iron is
Explanation of Solution
Explanation
The density of such a crystal is calculated by the formula,
Since,
The number of atoms in the unit cell is two when iron has the hcp structure.
The atomic mass of
Substitute these values in the formula of mass of the unit cell,
Similarly,
If silicon has hcp structure, then the number of atoms in the unit cell is two.
The atomic mass of silicon is
Substitute these values in the formula of mass of the unit cell,
Total mass of the crystal is the summation of
The volume of the crystal is
The density of the unit cell is calculated by the formula,
Substitute the values of mass and that of volume of the unit cell,
Therefore, the density of hcp iron is
Conclusion
The density of bcc iron is
Want to see more full solutions like this?
Chapter 12 Solutions
Smartwork5 Printed Access Card for Use with Chemistry: The Science in Context 5th Edition (SmartWork Access Printed Access Card)
- Predict the major products of this organic reaction. If there aren't any products, because nothing will happen, check the box under the drawing area instead. D ㄖˋ ید H No reaction. + 5 H₂O.* Click and drag to start drawing a structure. OH H₂Oarrow_forwardDraw one product of an elimination reaction between the molecules below. Note: There may be several correct answers. You only need to draw one of them. You do not need to draw any of the side products of the reaction 'O 10 + x 也 HO + 义 Click and drag to start drawing a structure.arrow_forwardWhat are the angles a and b in the actual molecule of which this is a Lewis structure? H- :0: C=N: b Note for advanced students: give the ideal angles, and don't worry about small differences from the ideal that might be caused by the fact that different electron groups may have slightly different sizes. a = 0° b=0 Xarrow_forward
- A student proposes the transformation below in one step of an organic synthesis. There may be one or more products missing from the right-hand side, but there are no reagents missing from the left-hand side. There may also be catalysts, small inorganic reagents, and other important reaction conditions missing from the arrow. • Is the student's transformation possible? If not, check the box under the drawing area. • If the student's transformation is possible, then complete the reaction by adding any missing products to the right-hand side, and adding required catalysts, inorganic reagents, or other important reaction conditions above and below the arrow. • You do not need to balance the reaction, but be sure every important organic reactant or product is shown. + This transformation can't be done in one step. T iarrow_forwardDetermine the structures of the missing organic molecules in the following reaction: H+ O OH H+ + H₂O ☑ ☑ Note: Molecules that share the same letter have the exact same structure. In the drawing area below, draw the skeletal ("line") structure of the missing organic molecule X. Molecule X shows up in multiple steps, but you only have to draw its structure once. Click and drag to start drawing a structure. X § ©arrow_forwardTable 1.1 Stock Standard Solutions Preparation. The amounts shown should be dissolved in 100 mL. Millipore water. Calculate the corresponding anion concentrations based on the actual weights of the reagents. Anion Amount of reagent (g) Anion Concentration (mg/L) 0.1649 Reagent Chloride NaCl Fluoride NaF 0.2210 Bromide NaBr 0.1288 Nitrate NaNO3 0.1371 Nitrite NaNO2 0.1500 Phosphate KH2PO4 0.1433 Sulfate K2SO4 0.1814arrow_forward
- Draw the structure of the pound in the provided CO as a 300-1200 37(2), 11 ( 110, and 2.5 (20arrow_forwardPlease help me with # 4 and 5. Thanks in advance!arrow_forwardA small artisanal cheesemaker is testing the acidity of their milk before it coagulates. During fermentation, bacteria produce lactic acid (K₁ = 1.4 x 104), a weak acid that helps to curdle the milk and develop flavor. The cheesemaker has measured that the developing mixture contains lactic acid at an initial concentration of 0.025 M. Your task is to calculate the pH of this mixture and determine whether it meets the required acidity for proper cheese development. To achieve the best flavor, texture and reduce/control microbial growth, the pH range needs to be between pH 4.6 and 5.0. Assumptions: Lactic acid is a monoprotic acid H H :0:0: H-C-C H :0: O-H Figure 1: Lewis Structure for Lactic Acid For simplicity, you can use the generic formula HA to represent the acid You can assume lactic acid dissociation is in water as milk is mostly water. Temperature is 25°C 1. Write the K, expression for the dissociation of lactic acid in the space provided. Do not forget to include state symbols.…arrow_forward
- Curved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electron-pushing arrows for the following reaction or mechanistic step(s). Be sure to account for all bond-breaking and bond-making steps. :0: :0 H. 0:0 :0: :6: S: :0: Select to Edit Arrows ::0 Select to Edit Arrows H :0: H :CI: Rotation Select to Edit Arrows H. < :0: :0: :0: S:arrow_forward3:48 PM Fri Apr 4 K Problem 4 of 10 Submit Curved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electron-pushing arrows for the following reaction or mechanistic step(s). Be sure to account for all bond-breaking and bond-making steps. Mg. :0: Select to Add Arrows :0: :Br: Mg :0: :0: Select to Add Arrows Mg. Br: :0: 0:0- Br -190 H 0:0 Select to Add Arrows Select to Add Arrows neutralizing workup H CH3arrow_forwardIarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





