
Concept explainers
(a)
Interpretation: The density of bcc iron when the radius of an iron atom is given to be
Concept introduction: The density of a unit cell is calculated by the formula,
The mass of a unit cell is calculated by the formula,
To determine: The density of bcc iron when the radius of an iron atom is
(a)
Answer to Problem 12.95AP
Solution
The density of bcc iron is
Explanation of Solution
Explanation
The density of bcc iron is calculated by the formula,
The number of atoms in the unit cell is two when iron has the bcc structure.
The
Substitute these values in the formula of mass of the unit cell,
The mass of bcc
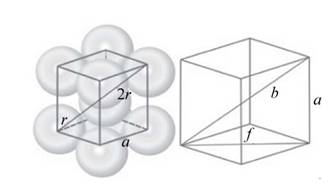
Figure 1
From Figure 1, the relationship between the radius of the iron sphere and the edge length of the unit cell is determined by the formula,
Face diagonal is calculated by the formula,
Body diagonal is calculated by the formula,
Thus, from equations (1) and (2),
The volume of the unit cell
Since,
The volume is calculated by the formula,
The volume of the unit cell in centimeters is,
The density of the unit cell is calculated by the formula,
Substitute the values of mass and that of volume of the unit cell,
Therefore, the density of bcc iron is
(b)
To determine: The density of hexagonal iron given a volume of unit cell is
(b)
Answer to Problem 12.95AP
Solution
The density of hcp iron is
Explanation of Solution
Explanation
The density of the hcp iron is calculated by the formula,
The number of atoms in the unit cell is two when iron has the hcp structure.
The atomic mass of
Substitute these values in the formula of mass of the unit cell,
The mass of hcp
The unit cell volume of hcp iron is given as
The density of the unit cell is calculated by the formula,
Substitute the values of mass and that of volume of the unit cell,
Therefore, the density of hcp iron is
(c)
To determine: The density of a crystal that has
(c)
Answer to Problem 12.95AP
Solution
The density of hcp iron is
Explanation of Solution
Explanation
The density of such a crystal is calculated by the formula,
Since,
The number of atoms in the unit cell is two when iron has the hcp structure.
The atomic mass of
Substitute these values in the formula of mass of the unit cell,
Similarly,
If silicon has hcp structure, then the number of atoms in the unit cell is two.
The atomic mass of silicon is
Substitute these values in the formula of mass of the unit cell,
Total mass of the crystal is the summation of
The volume of the crystal is
The density of the unit cell is calculated by the formula,
Substitute the values of mass and that of volume of the unit cell,
Therefore, the density of hcp iron is
Conclusion
The density of bcc iron is
Want to see more full solutions like this?
Chapter 12 Solutions
Chemistry: The Science in Context (Fifth Edition)
- Use diagram to answer the following: 1.Is the overall rxn endo- or exothermic. Explain briefly your answer____________________2. How many steps in this mechanism?_____________3. Which is the rate determining step? Explain briefly your answer____________________4. Identify (circle and label) the reactants,the products and intermediate (Is a Cation, Anion, or a Radical?) Please explain and provide full understanding.arrow_forwardDraw the entire mechanism and add Curved Arrows to show clearly how electrons areredistributed in the process. Please explain and provide steps clearly.arrow_forward15) Create Lewis structure Br Brarrow_forward
- LIOT S How would you make 200. mL of a 0.5 M solution of CuSO4 5H2O from solid copper (II) sulfate? View Rubricarrow_forwardSteps and explantions pleasearrow_forwardMatch the denticity to the ligand. Water monodentate ✓ C₂O2 bidentate H₂NCH₂NHCH2NH2 bidentate x EDTA hexadentate Question 12 Partially correct Mark 2 out of 2 Flag question Provide the required information for the coordination compound shown below: Na NC-Ag-CN] Number of ligands: 20 Coordination number: 2✔ Geometry: linear Oxidation state of transition metal ion: +3 x in 12 correct out of 2 question Provide the required information for the coordination compound shown below. Na NC-Ag-CN] Number of ligands: 20 Coordination number: 2 Geometry: linear 0 Oxidation state of transition metal ion: +3Xarrow_forward
- Can you explain step by step behind what the synthetic strategy would be?arrow_forwardPlease explain step by step in detail the reasoning behind this problem/approach/and answer. thank you!arrow_forward2. Predict the product(s) that forms and explain why it forms. Assume that any necessary catalytic acid is present. .OH HO H₂N OHarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





