
Concept explainers
If the null hypothesis is rejected in Exercises 1 through 8, use the Scheffé test when the
a. State the hypotheses and identify the claim.
b. Find the critical value(s).
c. Compute the test value.
d. Make the decision.
e. Summarize the results.
Use the traditional method of hypothesis testing unless otherwise specified.
1. Lengths of Various Types of Bridges The data represent the lengths in feet of three types of bridges in the United States. At a = 0.01, test the claim that there is no significant difference in the means of the lengths of the types of bridges.
| Simple truss | Segmented concrete | Continuous plate |
| 745 | 820 | 630 |
| 716 | 750 | 573 |
| 700 | 790 | 525 |
| 650 | 674 | 510 |
| 647 | 660 | 480 |
| 625 | 640 | 460 |
| 608 | 636 | 451 |
| 598 | 620 | 450 |
| 550 | 520 | 450 |
| 545 | 450 | 425 |
| 534 | 392 | 420 |
| 528 | 370 | 360 |
a.
To state: The hypothesis
To identify: The claim.
Answer to Problem 12.1.1RE
The hypothesis
The claim is that, all the means are same.
Explanation of Solution
Given info:
The data shows the lengths in feet of three types of bridges in the United States. The level of significance is 0.01.
Calculation:
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Here, all the means are same is tested. Hence, the claim is that, all the means are same.
b.
To find: The critical value.
Answer to Problem 12.1.1RE
The critical value is 5.285.
Explanation of Solution
Given info:
The level of significance is 0.01. The number of samples k is 3, the sample sizes
Calculation:
The degrees of freedom are
Where
Substitute 3 for k in
Substitute 36 for N and 3 for k in
Critical value:
The critical F-value is obtained using the Table H: The F-Distribution with the level of significance
Procedure:
- Locate 30 and 40 in the degrees of freedom, denominator row of the Table H.
- Obtain the value in the corresponding degrees of freedom, numerator column below 2.
That is,
That is, the critical value is 5.285.
Rejection region:
The null hypothesis would be rejected if
c.
To compute: The test value.
Answer to Problem 12.1.1RE
The test value is 6.94.
Explanation of Solution
Calculation:
Software procedure:
Step-by-step procedure to obtain the test statistic using the MINITAB software:
- Choose Stat > ANOVA > One-Way.
- In Response, enter the Temperatures.
- In Factor, enter the Factor.
- Click OK.
Output using the MINITAB software is given below:

From the MINITAB output, the test value F is 6.94.
d.
To make: The decision.
Answer to Problem 12.1.1RE
The null hypothesis is rejected.
Explanation of Solution
Conclusion:
From the result of part (c), the test value is 6.94.
Here, the F-statistic value is greater than the critical value.
That is,
Thus, it can be concluding that, the null hypothesis is rejected.
e.
To explain: The results.
Answer to Problem 12.1.1RE
The result concludes that, there is a significant difference between the means
Explanation of Solution
Calculation:
From the results, it can be observed that the null hypothesis is rejected. Thus, it can be concluding that there is evidence to reject the claim that all means are same.
Consider,
Step-by-step procedure to obtain the test mean and standard deviation using the MINITAB software:
- Choose Stat > Basic Statistics > Display Descriptive Statistics.
- In Variables enter the columns Florida, Pennsylvania and Maine.
- Choose option statistics, and select Mean, Variance and N total.
- Click OK.
Output using the MINITAB software is given below:
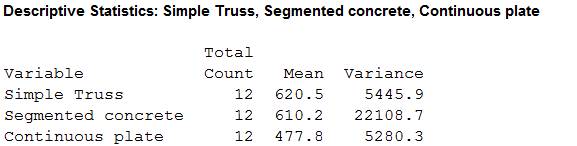
The sample sizes
The means are
The sample variances are
Here, the samples of sizes of three states are equal. So, the test used here is Tukey test.
Tukey test:
Critical value:
Here, k is 3 and degrees of freedom
Substitute 36 for N and 3 for k in v
The critical F-value is obtained using the Table N: Critical Values for the Tukey test with the level of significance
Procedure:
- Locate nearest value of 33 in the column of v of the Table H.
- Obtain the value in the corresponding row below 3.
That is, the critical value is 4.45.
Comparison of the means:
The formula for finding
That is,
Comparison between the means
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Rejection region:
The null hypothesis would be rejected if absolute value greater than the critical value.
Absolute value:
The formula for comparing the means
Substitute 620.5 and 610.2 for
Thus, the value of
Hence, the absolute value of
Conclusion:
The absolute value is 0.34.
Here, the absolute value is lesser than the critical value.
That is,
Thus, the null hypothesis is not rejected.
Hence, there is no significant difference between the means
Comparison between the means
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Rejection region:
The null hypothesis would be rejected if absolute value greater than the critical value.
Absolute value:
The formula for comparing the means
Substitute 620.5 and 477.8 for
Thus, the value of
Hence, the absolute value of
Conclusion:
The absolute value is 4.72.
Here, the absolute value is greater than the critical value.
That is,
Thus, the null hypothesis is rejected.
Hence, there is significant difference between the means
Comparison between the means
The hypotheses are given below:
Null hypothesis:
Alternative hypothesis:
Rejection region:
The null hypothesis would be rejected if absolute value greater than the critical value.
Absolute value:
The formula for comparing the means
Substitute 610.2 and 477.8 for
Thus, the value of
Hence, the absolute value of
Conclusion:
The absolute value is 4.38.
Here, the absolute value is lesser than the critical value.
That is,
Thus, the null hypothesis is not rejected.
Hence, there is no significant difference between the means
Want to see more full solutions like this?
Chapter 12 Solutions
Elementary Statistics: A Step By Step Approach
- II Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forwardwhy the answer is 3 and 10?arrow_forwardPS 9 Two films are shown on screen A and screen B at a cinema each evening. The numbers of people viewing the films on 12 consecutive evenings are shown in the back-to-back stem-and-leaf diagram. Screen A (12) Screen B (12) 8 037 34 7 6 4 0 534 74 1645678 92 71689 Key: 116|4 represents 61 viewers for A and 64 viewers for B A second stem-and-leaf diagram (with rows of the same width as the previous diagram) is drawn showing the total number of people viewing films at the cinema on each of these 12 evenings. Find the least and greatest possible number of rows that this second diagram could have. TIP On the evening when 30 people viewed films on screen A, there could have been as few as 37 or as many as 79 people viewing films on screen B.arrow_forward
- Q.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forwardThe table below indicates the number of years of experience of a sample of employees who work on a particular production line and the corresponding number of units of a good that each employee produced last month. Years of Experience (x) Number of Goods (y) 11 63 5 57 1 48 4 54 5 45 3 51 Q.1.1 By completing the table below and then applying the relevant formulae, determine the line of best fit for this bivariate data set. Do NOT change the units for the variables. X y X2 xy Ex= Ey= EX2 EXY= Q.1.2 Estimate the number of units of the good that would have been produced last month by an employee with 8 years of experience. Q.1.3 Using your calculator, determine the coefficient of correlation for the data set. Interpret your answer. Q.1.4 Compute the coefficient of determination for the data set. Interpret your answer.arrow_forwardCan you answer this question for mearrow_forward
- Techniques QUAT6221 2025 PT B... TM Tabudi Maphoru Activities Assessments Class Progress lIE Library • Help v The table below shows the prices (R) and quantities (kg) of rice, meat and potatoes items bought during 2013 and 2014: 2013 2014 P1Qo PoQo Q1Po P1Q1 Price Ро Quantity Qo Price P1 Quantity Q1 Rice 7 80 6 70 480 560 490 420 Meat 30 50 35 60 1 750 1 500 1 800 2 100 Potatoes 3 100 3 100 300 300 300 300 TOTAL 40 230 44 230 2 530 2 360 2 590 2 820 Instructions: 1 Corall dawn to tha bottom of thir ceraan urina se se tha haca nariad in archerca antarand cubmit Q Search ENG US 口X 2025/05arrow_forwardThe table below indicates the number of years of experience of a sample of employees who work on a particular production line and the corresponding number of units of a good that each employee produced last month. Years of Experience (x) Number of Goods (y) 11 63 5 57 1 48 4 54 45 3 51 Q.1.1 By completing the table below and then applying the relevant formulae, determine the line of best fit for this bivariate data set. Do NOT change the units for the variables. X y X2 xy Ex= Ey= EX2 EXY= Q.1.2 Estimate the number of units of the good that would have been produced last month by an employee with 8 years of experience. Q.1.3 Using your calculator, determine the coefficient of correlation for the data set. Interpret your answer. Q.1.4 Compute the coefficient of determination for the data set. Interpret your answer.arrow_forwardQ.3.2 A sample of consumers was asked to name their favourite fruit. The results regarding the popularity of the different fruits are given in the following table. Type of Fruit Number of Consumers Banana 25 Apple 20 Orange 5 TOTAL 50 Draw a bar chart to graphically illustrate the results given in the table.arrow_forward
- Q.2.3 The probability that a randomly selected employee of Company Z is female is 0.75. The probability that an employee of the same company works in the Production department, given that the employee is female, is 0.25. What is the probability that a randomly selected employee of the company will be female and will work in the Production department? Q.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forwardQ.2.1 A bag contains 13 red and 9 green marbles. You are asked to select two (2) marbles from the bag. The first marble selected will not be placed back into the bag. Q.2.1.1 Construct a probability tree to indicate the various possible outcomes and their probabilities (as fractions). Q.2.1.2 What is the probability that the two selected marbles will be the same colour? Q.2.2 The following contingency table gives the results of a sample survey of South African male and female respondents with regard to their preferred brand of sports watch: PREFERRED BRAND OF SPORTS WATCH Samsung Apple Garmin TOTAL No. of Females 30 100 40 170 No. of Males 75 125 80 280 TOTAL 105 225 120 450 Q.2.2.1 What is the probability of randomly selecting a respondent from the sample who prefers Garmin? Q.2.2.2 What is the probability of randomly selecting a respondent from the sample who is not female? Q.2.2.3 What is the probability of randomly…arrow_forwardTest the claim that a student's pulse rate is different when taking a quiz than attending a regular class. The mean pulse rate difference is 2.7 with 10 students. Use a significance level of 0.005. Pulse rate difference(Quiz - Lecture) 2 -1 5 -8 1 20 15 -4 9 -12arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning


