Chapter 12, Problem 12.117AP

(a)

Interpretation Introduction

Interpretation: The density of bcc iron when the radius of an iron atom is given to be $\text{126}\text{pm}$, the volume of unit cell is given to be $5.414\times {10}^{-23}{\text{cm}}^{\text{3}}$. The density of a crystal that has $4\%$ by mass of $\text{Si}$ is substituted for $\text{Fe}$ without changing the hcp crystal structure built on hexagonal unit cells is to be calculated.

Concept introduction: The density of a unit cell is calculated by the formula,

$\text{Density(d)}\text{of}\text{the}\text{unit}\text{cell}=\frac{\text{Mass(m)}\text{of}\text{the}\text{unit}\text{cell}}{\text{Volume(V)}\text{of}\text{the}\text{unit}\text{cell}}$

The mass of a unit cell is calculated by the formula,

$\text{Mass}\text{of}\text{the}\text{unit}\text{cell}=\text{Density}\text{of}\text{the}\text{unit}\text{cell}\times \text{volume}\text{of}\text{the}\text{unit}\text{cell}$

To determine: The density of bcc iron when the radius of an iron atom is $\text{126}\text{pm}$.

Answer to Problem 12.117AP

Solution

The density of bcc iron is $\underset{\_}{7.54g/c{m}^3}$.

Explanation of Solution

Explanation

The density of bcc iron is calculated by the formula,

$\begin{array}{l}\text{Density(d)}\text{of}\text{the}\text{unit}\text{cell}=\frac{\text{Mass(m)}\text{of}\text{the}\text{unit}\text{cell}}{\text{Volume(V)}\text{of}\text{the}\text{unit}\text{cell}}\\ \text{Mass}\text{of}\text{the}\text{unit}\text{cell}=\text{Density}\text{of}\text{the}\text{unit}\text{cell}\times \text{volume}\text{of}\text{the}\text{unit}\text{cell}\end{array}$

The number of atoms in the unit cell is two when iron has the bcc structure.

The atomic mass of $\text{Fe}$ is $\text{55}\text{.84}\text{g}/\text{mol}$.

Substitute these values in the formula of mass of the unit cell,

$\begin{array}{c}\text{Mass}\text{of}\text{Fe}\text{unit}\text{cell}=\frac{\text{55}\text{.84}\text{g}}{\text{1}\text{mol}}\times \frac{\text{1}\text{mol}}{\text{6}\text{.023}\times {\text{10}}^{\text{23}}\text{atoms}}\times \text{2}\text{atoms}\\ =\text{1}\text{.854}\times {\text{10}}^{\text{-22}}\text{g}\end{array}$

The mass of bcc $\text{Fe}$ unit cell is $\text{1}{\text{.854×10}}^{\text{-22}}\text{g}$

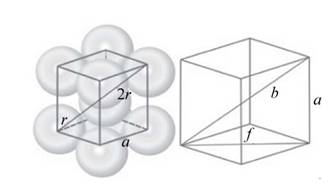
Figure 1

From Figure 1, the relationship between the radius of the iron sphere and the edge length of the unit cell is determined by the formula,

$b=4r$ (1)

Face diagonal is calculated by the formula,

$\begin{array}{l}{f}^2=a^2+a^2\\ f=a\sqrt{2}\end{array}$

Body diagonal is calculated by the formula,

$\begin{array}{c}{b}^2=f^2+a^2\\ =3a^2\\ =a\sqrt{3}\end{array}$ (2)

Thus, from equations (1) and (2),

$\begin{array}{c}4r=a\sqrt{3}\\ a=\frac{4r}{\sqrt{3}}\end{array}$

The volume of the unit cell $\left(V\right)$ is $a^3$, where $a$ is the edge length of the unit cell.

Since, $a=\frac{4r}{\sqrt{3}}$

The volume is calculated by the formula,

$\begin{array}{c}V={(}^a\\ ={\left(\frac{4r}{\sqrt{3}}\right)}^3\\ =\frac{64r^3}{3\sqrt{3}}\end{array}$

The volume of the unit cell in centimeters is,

$\begin{array}{c}V=\frac{64r^3}{3\sqrt{3}}\\ =\frac{64}{3\sqrt{3}}{\left(126\text{pm}\right)}^3\times \frac{{\left({10}^{-10}\text{cm}\right)}^3}{{\text{pm}}^{\text{3}}}\\ =2.46\times {10}^{-23}{\text{cm}}^3\end{array}$

The density of the unit cell is calculated by the formula,

$d=\frac{m}{V}$

Substitute the values of mass and that of volume of the unit cell,

$\begin{array}{c}d=\frac{1.854\times {10}^{-22}\text{g}}{2.46\times {10}^{-23}{\text{cm}}^{\text{3}}}\\ =\underset{\_}{7.54g/c{m}^3}\end{array}$

Therefore, the density of bcc iron is $\underset{\_}{7.54g/c{m}^3}$.

(b)

Interpretation Introduction

To determine: The density of hexagonal iron given a volume of unit cell is $5.414\times {10}^{-23}{\text{cm}}^{\text{3}}$.

Answer to Problem 12.117AP

Solution

The density of hcp iron is $\underset{\_}{3.42g/c{m}^3}$.

Explanation of Solution

Explanation

The density of the hcp iron is calculated by the formula,

$\begin{array}{l}\text{Density(d)}\text{of}\text{the}\text{unit}\text{cell}=\frac{\text{Mass(m)}\text{of}\text{the}\text{unit}\text{cell}}{\text{Volume(V)}\text{of}\text{the}\text{unit}\text{cell}}\\ \text{Mass}\text{of}\text{the}\text{unit}\text{cell}=\text{Density}\text{of}\text{the}\text{unit}\text{cell}\times \text{volume}\text{of}\text{the}\text{unit}\text{cell}\end{array}$

The number of atoms in the unit cell is two when iron has the hcp structure.

The atomic mass of $\text{Fe}$ is $\text{55}\text{.84}\text{g}/\text{mol}$.

Substitute these values in the formula of mass of the unit cell,

$\begin{array}{c}\text{Mass}\text{of}\text{Fe}\text{unit}\text{cell}=\frac{\text{55}\text{.84}\text{g}}{\text{1}\text{mol}}\times \frac{\text{1}\text{mol}}{\text{6}\text{.023}\times {\text{10}}^{\text{23}}\text{atoms}}\times \text{2}\text{atoms}\\ =\text{1}\text{.854}\times {\text{10}}^{\text{-22}}\text{g}\end{array}$

The mass of hcp $\text{Fe}$ unit cell is $\text{1}{\text{.854×10}}^{\text{-22}}\text{g}$

The unit cell volume of hcp iron is given as $5.414\times {10}^{-23}{\text{cm}}^{\text{3}}$

The density of the unit cell is calculated by the formula,

$d=\frac{m}{V}$

Substitute the values of mass and that of volume of the unit cell,

$\begin{array}{c}d=\frac{1.854\times {10}^{-22}\text{g}}{5.414\times {10}^{-23}{\text{cm}}^{\text{3}}}\\ =\underset{\_}{3.42g/c{m}^3}\end{array}$

Therefore, the density of hcp iron is $\underset{\_}{3.42g/c{m}^3}$.

(c)

Interpretation Introduction

To determine: The density of a crystal that has $4\%$ by mass of $\text{Si}$ is substituted for $\text{Fe}$ without changing the hcp crystal structure built on hexagonal unit cells.

Answer to Problem 12.117AP

Solution

The density of hcp iron is $\underset{\_}{3.36g/c{m}^3}$.

Explanation of Solution

Explanation

The density of such a crystal is calculated by the formula,

$\begin{array}{l}\text{Density(d)}\text{of}\text{the}\text{unit}\text{cell}=\frac{\text{Mass(m)}\text{of}\text{the}\text{unit}\text{cell}}{\text{Volume(V)}\text{of}\text{the}\text{unit}\text{cell}}\\ \text{Mass}\text{of}\text{the}\text{unit}\text{cell}=\text{Density}\text{of}\text{the}\text{unit}\text{cell}\times \text{volume}\text{of}\text{the}\text{unit}\text{cell}\end{array}$

Since, $4\%$ by mass of $\text{Si}$ is substituted for $\text{Fe}$ without changing the hcp structure. Hence, total mass of crystal is the summation of $96\%$ mass of iron and $4\%$ mass of silicon.

The number of atoms in the unit cell is two when iron has the hcp structure.

The atomic mass of $\text{Fe}$ is $\text{55}\text{.84}\text{g}/\text{mol}$.

Substitute these values in the formula of mass of the unit cell,

$\begin{array}{c}\text{Mass}\text{of}\text{Fe}\text{unit}\text{cell}=\frac{\text{55}\text{.84}\text{g}}{\text{1}\text{mol}}\times \frac{\text{1}\text{mol}}{\text{6}\text{.023}\times {\text{10}}^{\text{23}}\text{atoms}}\times \text{2}\text{atoms}\\ =\text{1}\text{.854}\times {\text{10}}^{\text{-22}}\text{g}\end{array}$

Similarly,

If silicon has hcp structure, then the number of atoms in the unit cell is two.

The atomic mass of silicon is $28.0\text{8}\text{g}/\text{mol}$.

Substitute these values in the formula of mass of the unit cell,

$\begin{array}{c}\text{Mass}\text{of}\text{Si}\text{unit}\text{cell}=\frac{28.08\text{g}}{\text{1}\text{mol}}\times \frac{\text{1}\text{mol}}{\text{6}\text{.023}\times {\text{10}}^{\text{23}}\text{atoms}}\times \text{2}\text{atoms}\\ =0.932\times {\text{10}}^{\text{-22}}\text{g}\end{array}$

Total mass of the crystal is the summation of $96\%$ mass of iron and $4\%$ mass of silicon.

$\left(\frac{96}{100}\times 1.854\times {10}^{-22}\text{g}\right)+\left(\frac{4}{100}\times 0.932\times {10}^{-22}\text{g}\right)=1.816\times {10}^{-22}\text{g}$

The volume of the crystal is $5.414\times {10}^{-23}{\text{cm}}^3$.

The density of the unit cell is calculated by the formula,

$d=\frac{m}{V}$

Substitute the values of mass and that of volume of the unit cell,

$\begin{array}{c}d=\frac{1.816\times {10}^{-22}\text{g}}{5.414\times {10}^{-23}{\text{cm}}^{\text{3}}}\\ =\underset{\_}{3.36g/c{m}^3}\end{array}$

Therefore, the density of hcp iron is $\underset{\_}{3.42g/c{m}^3}$.

Conclusion

The density of bcc iron is $\underset{\_}{7.54g/c{m}^3}$, the density of hcp iron is $\underset{\_}{3.42g/c{m}^3}$ and the density of hcp iron when $4\%$ by mass of $\text{Si}$ is substituted for $\text{Fe}$ without changing the hcp crystal structure built on hexagonal unit cells is $\underset{\_}{3.42g/c{m}^3}$