Pearson eText for Thinking Mathematically -- Instant Access (Pearson+)
Pearson eText for Thinking Mathematically -- Instant Access (Pearson+)
7th Edition
ISBN: 9780137502240
Author: ROBERT BLITZER
Publisher: PEARSON+
bartleby

Concept explainers

Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear re…
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
bartleby

Videos

Textbook Question
Book Icon
Chapter 11.7, Problem 7E

Exercises 1-26 involve probabilities with independent events.

Use the spinner shown to solve Exercises 1-10. It is equally probable that the pointer will land on any one of the six regions. If the pointer lands on a borderline, spin again. If the pointer is spun twice, find the probability it will land on

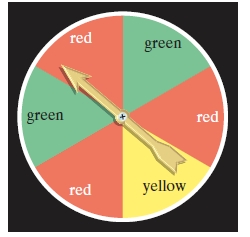
Chapter 11.7, Problem 7E, Exercises 1-26 involve probabilities with independent events. Use the spinner shown to solve

If the pointer is spun three times, find the probability it will land on

green and then red and then yellow.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 11.7, Problem 6E
Next
Chapter 11.7, Problem 8E
Students have asked these similar questions
3. Construct a triangle in the Poincare plane with all sides equal to ln(2).   (Hint: Use the fact that, the circle with center (0,a) and radius ln(r), r>1 in    the Poincaré plane is equal to the point set       { (x,y) : x^2+(y-1/2(r+1/r)a)^2=1/4(r-1/r)^2a^2 }
n. g. = neutral geometry  <ABC  = angle ABC \leq  = less or equal than sqrt{x} = square root of x cLr = the line in the Poincaré plane defined by the equation (x-c)^2+y^2=r^2 1. Find the bisector of the angle <ABC in the Poincaré plane, where    A=(0,5), B=(0,3) and C=(2,\sqrt{21})
Task: 2 Multivariable Calculus: Divergence Theorem Refer to Question 42 in the provided document. Link: https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing

Chapter 11 Solutions

Pearson eText for Thinking Mathematically -- Instant Access (Pearson+)

Ch. 11.1 - CHECK POINT 1 A restaurant offers 10 appetizers...Ch. 11.1 - CHECK POINT 2 Rework Example 2 given that the...Ch. 11.1 - CHECK POINT 3 A pizza can be ordered with two...Ch. 11.1 - CHECK POINT 4 The car in Example 4 is now...Ch. 11.1 - CHECK POINT 5 You are taking a multiple-choice...Ch. 11.1 - CHECK POINT 6 An electronic gate can be opened by...Ch. 11.1 - Fill in each blank so that the resulting statement...Ch. 11.1 - 2. The number of ways in which a series of...Ch. 11.1 - In Exercises 3-4, determine whether each statement...Ch. 11.1 - In Exercises 3-4, determine whether each statement...
Ch. 11.1 - Practice and Application Exercises A restaurant...Ch. 11.1 - The model of the car you are thinking of buying is...Ch. 11.1 - a popular brand 0f pen is available in three...Ch. 11.1 - 4. In how many ways can a casting director choose...Ch. 11.1 - A student is planning a two-part trip. The first...Ch. 11.1 - 6. For a temporary job between semesters, you are...Ch. 11.1 - An ice cream store sells two drinks (sodas or milk...Ch. 11.1 - A pizza can be ordered with three choices of size...Ch. 11.1 - A restaurant offers the following limited lunch...Ch. 11.1 - An apartment complex offers apartments with four...Ch. 11.1 - 11. Shoppers in a large shopping mall are...Ch. 11.1 - 12. There are three highways from city A to city...Ch. 11.1 - 13. A person can order a new car with a choice of...Ch. 11.1 - A car model comes in nine colors, with or without...Ch. 11.1 - 15. You are taking a multiple-choice test that has...Ch. 11.1 - You are taking a multiple-choice test that has...Ch. 11.1 - 17. In the original plan for area codes in...Ch. 11.1 - 18. The local seven-digit telephone numbers in...Ch. 11.1 - 19. License plates in a particular slate display...Ch. 11.1 - 20. How many different four-letter radio station...Ch. 11.1 - A stock can go up, go down, or stay unchanged. How...Ch. 11.1 - 22. A social security number contains nine digits,...Ch. 11.1 - 23. Explain the Fundamental Counting Principle Ch. 11.1 - Figure 11.2 on page 689 shows that a tree diagram...Ch. 11.1 - 25. Write an original problem that can be solved...Ch. 11.1 - Prob. 26ECh. 11.1 - Make Sense? In Exercises 26-29, determine whether...Ch. 11.1 - Make Sense? In Exercises 26-29, determine whether...Ch. 11.1 - 29. There are more than 2000 possible sets of...Ch. 11.1 - 30. How many four-digit odd numbers are there?...Ch. 11.1 - In order to develop a more appealing hamburger, a...Ch. 11.2 - CHECK POINT 1 How many ways can the six jokes...Ch. 11.2 - CHECK POINT 2 In how many ways can you arrange...Ch. 11.2 - CHECK POINT 3 Evaluate without using a...Ch. 11.2 - CHECK POINT4 A corporation has seven members on...Ch. 11.2 - CHECK POINT 5 How many different programming...Ch. 11.2 - In how many ways can the letters of the word...Ch. 11.2 - Ch. 11.2 - Fill in each blank so that the resulting statement...Ch. 11.2 - Fill in each blank so that the resulting statement...Ch. 11.2 - Fill in each blank so that the resulting statement...Ch. 11.2 - Fill in each blank so that the resulting statement...Ch. 11.2 - Fill in each blank so that the resulting statement...Ch. 11.2 - Fill in each blank so that the resulting statement...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Prob. 7ECh. 11.2 - Prob. 8ECh. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - Use the Fundamental Counting Principle to solve...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 13-32, evaluate each factorial...Ch. 11.2 - In Exercises 33-40, use the formula for to...Ch. 11.2 - In Exercises 33-40, use the formula for to...Ch. 11.2 - Prob. 35ECh. 11.2 - In Exercises 33-40, use the formula for n P r to...Ch. 11.2 - In Exercises 33-40, use the formula for n P r to...Ch. 11.2 - In Exercises 33-40, use the formula for n P r to...Ch. 11.2 - In Exercises 33-40, use the formula for to...Ch. 11.2 - In Exercises 33-40, use the formula for to...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - In a race in which six automobiles are entered and...Ch. 11.2 - Prob. 46ECh. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Use an appropriate permutations formula to solve...Ch. 11.2 - Prob. 57ECh. 11.2 - Prob. 58ECh. 11.2 - 59. Explain the best way to evaluate without a...Ch. 11.2 - Prob. 60ECh. 11.2 - Write a word problem that can be solved by...Ch. 11.2 - 62. Write a word problem that can be solved by...Ch. 11.2 - If 24 permutations can be formed using the letters...Ch. 11.2 - Prob. 64ECh. 11.2 - Prob. 65ECh. 11.2 - Prob. 66ECh. 11.2 - Make Sense? In Exercises 64-67, determine whether...Ch. 11.2 - Prob. 68ECh. 11.2 - Prob. 69ECh. 11.2 - Prob. 70ECh. 11.2 - Five men and five women line up at a checkout...Ch. 11.2 - How many four-digit odd numbers less than 6000 can...Ch. 11.2 - Prob. 73ECh. 11.3 - CHECK POINT 1 For each of the following problems,...Ch. 11.3 - CHECK POINT 2 You volunteer to pet-sit for your...Ch. 11.3 - CHECK POINT 3 How many different 4-card hands can...Ch. 11.3 - CHECK POINT 4 A zoo has six male bears and seven...Ch. 11.3 - Fill in each blank so that the resulting statement...Ch. 11.3 - Fill in each blank so that the resulting statement...Ch. 11.3 - Fill in each blank so that the resulting statement...Ch. 11.3 - Fill in each blank so that the resulting statement...Ch. 11.3 - 1. A medical researcher needs 6 people to test the...Ch. 11.3 - In Exercises 1-4, does the problem involve...Ch. 11.3 - In Exercises 1-4, does the problem involve...Ch. 11.3 - In Exercises 1-4, does the problem involve...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for to...Ch. 11.3 - In Exercises 5-20, use the formula for to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - Prob. 14ECh. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for to...Ch. 11.3 - In Exercises 5-20, use the formula for to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 5-20, use the formula for n C r to...Ch. 11.3 - In Exercises 21-28, evaluate each expression. 21....Ch. 11.3 - Prob. 22ECh. 11.3 - In Exercises 21-28, evaluate each expression. 1 −...Ch. 11.3 - In Exercises 21-28, evaluate each expression. 1 −...Ch. 11.3 - In Exercises 21-28, evaluate each expression. 25....Ch. 11.3 - In Exercises 21-28, evaluate each expression. 26....Ch. 11.3 - Prob. 27ECh. 11.3 - In Exercises 21-28, evaluate each expression 5 C 1...Ch. 11.3 - Use the formula for n C r to solve Exercises...Ch. 11.3 - Use the formula for to solve Exercises 29-40. 30....Ch. 11.3 - Use the formula for n C r to solve Exercises...Ch. 11.3 - Use the formula for to solve Exercises 29-40. 32....Ch. 11.3 - Use the formula for n C r to solve Exercises...Ch. 11.3 - Use the formula for n C r to solve Exercises...Ch. 11.3 - 35. To win at LOTTO in the slate of Florida, one...Ch. 11.3 - Use the formula for n C r to solve Exercises...Ch. 11.3 - Use the formula for to solve Exercises 29-40. 37....Ch. 11.3 - Use the formula for to solve Exercises 29-40. 38....Ch. 11.3 - Use the formula for n C r to solve Exercises...Ch. 11.3 - Use the formula for to solve Exercises 29-40. 40....Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - Prob. 43ECh. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - Prob. 45ECh. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - Prob. 49ECh. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - Prob. 53ECh. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - Prob. 57ECh. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - In Exercises 41-60, solve by the method of your...Ch. 11.3 - Thousands of jokes have been told about marriage...Ch. 11.3 - Thousands of jokes have been told about marriage...Ch. 11.3 - Prob. 63ECh. 11.3 - Thousands of jokes have been told about marriage...Ch. 11.3 - Prob. 65ECh. 11.3 - Prob. 66ECh. 11.3 - Thousands of jokes have been told about marriage...Ch. 11.3 - Thousands of jokes have been told about marriage...Ch. 11.3 - Prob. 69ECh. 11.3 - Explain how to distinguish between permutation and...Ch. 11.3 - 71. Write a word problem that can be solved by...Ch. 11.3 - Make Sense? In Exercises 72-75, determine whether...Ch. 11.3 - Make Sense? In Exercises 72-75, determine whether...Ch. 11.3 - Prob. 74ECh. 11.3 - Prob. 75ECh. 11.3 - Prob. 76ECh. 11.3 - 77. A 6/53 lottery involves choosing 6 of the...Ch. 11.3 - Prob. 78ECh. 11.3 - Prob. 79ECh. 11.3 - Prob. 80ECh. 11.4 - CHECKPOINT I A die is rolled once. Find the...Ch. 11.4 - CHECK POINT 2 You are dealt one card from a...Ch. 11.4 - CHECK POINT 3 Use Table 11.2 in Example 3 to solve...Ch. 11.4 - CHECK POINT 4 If one person is randomly selected...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - Fill in each blank so that the resulting statement...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - a number greater than 4. In Exercises 1-54,...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 1-54, express each probability as a...Ch. 11.4 - In Exercises 21-26, a fair coin is tossed two...Ch. 11.4 - Exercises 21-26, a fair coin is tossed two times...Ch. 11.4 - In Exercises 21-26, a fair coin is tossed two...Ch. 11.4 - In Exercises 21-26, a fair coin is tossed two...Ch. 11.4 - In Exercises 21-26, a fair coin is tossed two...Ch. 11.4 - In Exercises 21-26, a fair coin is tossed two...Ch. 11.4 - In Exercises 27-34, you select a family with three...Ch. 11.4 - In Exercises 27-34, you select a family with three...Ch. 11.4 - Prob. 29ECh. 11.4 - In Exercises 27-34, you select a family with three...Ch. 11.4 - In Exercises 27-34, you select a family with three...Ch. 11.4 - In Exercises 27-34, you select a family with three...Ch. 11.4 - Prob. 33ECh. 11.4 - In Exercises 27-34, you select a family with three...Ch. 11.4 - In Exercises 35-40, a single die is rolled twice....Ch. 11.4 - In Exercises 35-40, a single die is rolled twice....Ch. 11.4 - In Exercises 35-40, a single die is rolled twice....Ch. 11.4 - In Exercises 35-40, a single die is rolled twice....Ch. 11.4 - In Exercises 35-40, a single die is rolled twice....Ch. 11.4 - In Exercises 35-40, a single die is rolled twice....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Use the spinner shown to answer Exercises 41-48....Ch. 11.4 - Prob. 49ECh. 11.4 - Exercises 49-54 deal with sickle cell anemia, an...Ch. 11.4 - Exercises 49-54 deal with sickle cell anemia, an...Ch. 11.4 - Exercises 49-54 deal with sickle cell anemia, an...Ch. 11.4 - Prob. 53ECh. 11.4 - Exercises 49-54 deal with sickle cell anemia, an...Ch. 11.4 - The Table shows the distribution, by age and...Ch. 11.4 - The table shows the distribution, by age and...Ch. 11.4 - The table shows the distribution, by age and...Ch. 11.4 - The table shows the distribution, by age and...Ch. 11.4 - The table shows the distribution, by age and...Ch. 11.4 - The table shows the distribution, by age and...Ch. 11.4 - The table shows the number of Americans who moved...Ch. 11.4 - The table shows the number of Americans who moved...Ch. 11.4 - Prob. 63ECh. 11.4 - The table shows the number of Americans who moved...Ch. 11.4 - The table shows the number of Americans who moved...Ch. 11.4 - The table shows the number of Americans who moved...Ch. 11.4 - The table shows the educational attainment of the...Ch. 11.4 - The table shows the educational attainment of the...Ch. 11.4 - The table shows the educational attainment of the...Ch. 11.4 - Prob. 70ECh. 11.4 - What is the sample space of an experiment? What is...Ch. 11.4 - 72. How is the theoretical probability of an event...Ch. 11.4 - Prob. 73ECh. 11.4 - Prob. 74ECh. 11.4 - Prob. 75ECh. 11.4 - Prob. 76ECh. 11.4 - Prob. 77ECh. 11.4 - 78. The president of a large company with 10,000...Ch. 11.4 - Make Sense? In Exercises 79-82, determine whether...Ch. 11.4 - Prob. 80ECh. 11.4 - Make Sense? In Exercises 79-82, determine whether...Ch. 11.4 - Prob. 82ECh. 11.4 - Prob. 83ECh. 11.4 - Some three-digit numbers, such as 101 and 313,...Ch. 11.5 - CHECK POINT I Consider the six jokes about books...Ch. 11.5 - CHECK POINT 2 Hitting the jackpot in Powerball is...Ch. 11.5 - CHECK POINT 3 A club consists of six men and four...Ch. 11.5 - Fill in each blank so that the resulting statement...Ch. 11.5 - Fill in each blank so that the resulting statement...Ch. 11.5 - Fill in each blank so that the resulting statement...Ch. 11.5 - Fill in each blank so that the resulting statement...Ch. 11.5 - Martha, Lee, Nancy, Paul, and Armando have all...Ch. 11.5 - Three men and three women line up al a checkout...Ch. 11.5 - 3. Six stand-up comics. A, B, C, D, E, and F, are...Ch. 11.5 - 4. Seven performers, A, B, C, D, E, F, and G, are...Ch. 11.5 - A group consists of four men and five women. Three...Ch. 11.5 - A political discussion group consists of five...Ch. 11.5 - Mega Millions is a multi-state lottery played in...Ch. 11.5 - Mega Millions is a multi-state lottery played in...Ch. 11.5 - Mega Millions is a multi-state lottery played in...Ch. 11.5 - Mega Millions is a multi-state lottery played in...Ch. 11.5 - 11. A box contains 25 transistors, 6 of which are...Ch. 11.5 - A committee of five people is to be formed from...Ch. 11.5 - 13. A city council consists of six Democrats and...Ch. 11.5 - 14. A parent-teacher committee consisting of four...Ch. 11.5 - Exercises 15-20 involve a deck of 52 cards. If...Ch. 11.5 - Exercises 15-20 involve a deck of 52 cards. If...Ch. 11.5 - Exercises 15-20 involve a deck of 52 cards. If...Ch. 11.5 - Exercises 15-20 involve a deck of 52 cards. If...Ch. 11.5 - Exercises 15-20 involve a deck of 52 cards. If...Ch. 11.5 - Exercises 15-20 involve a deck of 52 cards. If...Ch. 11.5 - If people understood the mathematics involving...Ch. 11.5 - 22. Write and solve an original problem involving...Ch. 11.5 - 23. Write and solve an original problem involving...Ch. 11.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 11.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 11.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 11.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 11.5 - 28. An apartment complex offers apartments with...Ch. 11.5 - 29. Suppose that it is a drawing in which the...Ch. 11.5 - The digits 1, 2, 3, 4, and 5 are randomly arranged...Ch. 11.5 - 31. In a five-card poker hand, what is the...Ch. 11.5 - Research and present a group report on state and...Ch. 11.6 - CHECKPOINT 1 If you are dealt one card from a...Ch. 11.6 - CHECK POINT 2 Use the data in Figure 11.6 to find...Ch. 11.6 - CHECK POINT 3 If one driver is randomly selected...Ch. 11.6 - CHECK POINT 3 If you roll a single, six-sided die....Ch. 11.6 - CHECK POINT4 In a group of 50 sludents.23 lake...Ch. 11.6 - CHECK POINT 5 Use Figure 11.10 to find the...Ch. 11.6 - CHECK POINT 6 If one person is randomly selected...Ch. 11.6 - CHECK POINT 7 You are dealt one card from a...Ch. 11.6 - CHECK POINT 8 The winner of a raffle will receive...Ch. 11.6 - CHECK POINT 9 The odds against a particular horse...Ch. 11.6 - 1. Because Ch. 11.6 - Prob. 2CVCCh. 11.6 - 3. If it is possible for events A and B to occur...Ch. 11.6 - Prob. 4CVCCh. 11.6 - Prob. 5CVCCh. 11.6 - In Exercises 6-9, determine whether each statement...Ch. 11.6 - In Exercises 6-9, determine whether each statement...Ch. 11.6 - In Exercises 6-9, determine whether each statement...Ch. 11.6 - In Exercises 6-9, determine whether each statement...Ch. 11.6 - In Exercises 1-6, you are dealt one card from a 52...Ch. 11.6 - In Exercises 1-6, you are dealt one card from a 52...Ch. 11.6 - In Exercises 1-6, you are dealt one card from a...Ch. 11.6 - In Exercises 1-6, you are dealt one card from a...Ch. 11.6 - In Exercises 1-6, you are dealt one card from a...Ch. 11.6 - In Exercises 1-6, you are dealt one card from a...Ch. 11.6 - In 5-card poker, played with a standard 52-card...Ch. 11.6 - In 5-card poker, played with a standard 52-eatd...Ch. 11.6 - In 5-card poker, played with a standard 52-eatd...Ch. 11.6 - In 5-card poker, played with a standard 52-eatd...Ch. 11.6 - The graph shows the probability of cardiovascular...Ch. 11.6 - The graph shows the probability of cardiovascular...Ch. 11.6 - The table shows the distribution, by age, of a...Ch. 11.6 - The table shows the distribution, by age, of a...Ch. 11.6 - The table shows the distribution, by age, of a...Ch. 11.6 - The table shows the distribution, by age, of a...Ch. 11.6 - In Exercises 17-22, you randomly select one card...Ch. 11.6 - In Exercises 17-22, you randomly select one card...Ch. 11.6 - In Exercises 17-22, you randomly select one card...Ch. 11.6 - In Exercises 17-22, you randomly select one card...Ch. 11.6 - In Exercises 17-22, you randomly select one card...Ch. 11.6 - In Exercises 17-22, you randomly select one card...Ch. 11.6 - Prob. 23ECh. 11.6 - 24. A political discussion group consists of 30...Ch. 11.6 - In Exercises 25-26, a single die is rolled. Find...Ch. 11.6 - In Exercises 25-26, a single die is rolled. Find...Ch. 11.6 - In Exercises 27-30, you are dealt one card from a...Ch. 11.6 - In Exercises 27-30, you are dealt one card from a...Ch. 11.6 - In Exercises 27-30, you are dealt one card from a...Ch. 11.6 - In Exercises 27-30, you are dealt one card from a...Ch. 11.6 - In Exercises 31-34, it is equally probable that...Ch. 11.6 - In Exercises 31-34, it is equally probable that...Ch. 11.6 - In Exercises 31-34, it is equally probable that...Ch. 11.6 - In Exercises 31-34, it is equally probable that...Ch. 11.6 - Use this information to solve Exercises 35-38. The...Ch. 11.6 - Use this information to solve Exercises 35-38. The...Ch. 11.6 - Use this information to solve Exercises 35-38. The...Ch. 11.6 - Use this information to solve Exercises 35-38. The...Ch. 11.6 - Prob. 39ECh. 11.6 - A student is selected at random from a group of...Ch. 11.6 - The table shows the educational attainment of the...Ch. 11.6 - The table shows the educational attainment of the...Ch. 11.6 - Prob. 43ECh. 11.6 - The table shows the educational attainment of the...Ch. 11.6 - The table shows the educational attainment of the...Ch. 11.6 - 46. has completed four years of high school only...Ch. 11.6 - Find the odds in favor and the odds against a...Ch. 11.6 - Find the odds in favor and the odds against a...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 49-58, one tile is drawn from...Ch. 11.6 - In Exercises 59-62, refer to the diagram showing...Ch. 11.6 - In Exercises 59-62, refer to the diagram showing...Ch. 11.6 - In Exercises 59-62, refer to the diagram showing...Ch. 11.6 - In Exercises 59-62, refer to the diagram showing...Ch. 11.6 - In Exercises 61-64, a single die is rolled. Find...Ch. 11.6 - In Exercises 61-64, a single die is rolled. Find...Ch. 11.6 - In Exercises 61-64, a single die is rolled. Find...Ch. 11.6 - Prob. 66ECh. 11.6 - The circle graphs show the percentage of...Ch. 11.6 - The circle graphs show the percentage of...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - In Exercises 67-76, one card is randomly selected...Ch. 11.6 - 77. The winner of a raffle will receive a 21-foot...Ch. 11.6 - The winner of a raffle will receive a 30-day...Ch. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Prob. 84ECh. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Of the 38 plays attributed to Shakespeare, 18 are...Ch. 11.6 - Prob. 89ECh. 11.6 - If you are given odds of 3 to 7 in favor of...Ch. 11.6 - Prob. 91ECh. 11.6 - 90. The odds in favor of a person who is alive at...Ch. 11.6 - Exercises 91-92 give the odds against various...Ch. 11.6 - Exercises 91-92 give the odds against various...Ch. 11.6 - Prob. 95ECh. 11.6 - What are mutually exclusive events? Give an...Ch. 11.6 - Explain how to find or probabilities with mutually...Ch. 11.6 - Prob. 98ECh. 11.6 - Prob. 99ECh. 11.6 - Prob. 100ECh. 11.6 - Prob. 101ECh. 11.6 - Make Sense? In Exercises 100-103, determine...Ch. 11.6 - Make Sense? In Exercises 100-103, determine...Ch. 11.6 - The probability of selecting a king or a heart...Ch. 11.6 - Make Sense? In Exercises 100-103, determine...Ch. 11.6 - Prob. 106ECh. 11.6 - Prob. 107ECh. 11.6 - Prob. 108ECh. 11.7 - CHECKPOINT 1 Find the probability of green...Ch. 11.7 - CHECK POINT 2 Find the probability of a family...Ch. 11.7 - Prob. 3CPCh. 11.7 - Prob. 4CPCh. 11.7 - Prob. 5CPCh. 11.7 - CHECK POINT 6 A letter is randomly selected from...Ch. 11.7 - Prob. 7CPCh. 11.7 - $$ CHECKPOINT 8 Use the data in Table 11.7 on the...Ch. 11.7 - Fill in each blank so that the resulting statement...Ch. 11.7 - Fill in each blank so that the resulting statement...Ch. 11.7 - Prob. 3CVCCh. 11.7 - Prob. 4CVCCh. 11.7 - In Exercises 5-8, determine whether each statement...Ch. 11.7 - Prob. 6CVCCh. 11.7 - Prob. 7CVCCh. 11.7 - Prob. 8CVCCh. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - Exercises 1-26 involve probabilities with...Ch. 11.7 - In Exercises 11-14, a single die is rolled twice....Ch. 11.7 - In Exercises 11-14, a single die is rolled twice....Ch. 11.7 - In Exercises 11-14, a single die is rolled twice....Ch. 11.7 - In Exercises 11-14, a single die is rolled twice....Ch. 11.7 - In Exercises 15-20, you draw one card from a...Ch. 11.7 - In Exercises 15-20, you draw one card from a...Ch. 11.7 - In Exercises 15-20, you draw one card from a...Ch. 11.7 - In Exercises 15-20, you draw one card from a...Ch. 11.7 - In Exercises 15-20, you draw one card from a...Ch. 11.7 - In Exercises 15-20, you draw one card from a...Ch. 11.7 - If you toss a fair coin six times, what is the...Ch. 11.7 - If you toss a fair coin seven times, what is the...Ch. 11.7 - In Exercises 23-24, a coin is tossed and a die is...Ch. 11.7 - In Exercises 23-24, a coin is tossed and a die is...Ch. 11.7 - The probability that South Florida will be hit by...Ch. 11.7 - 26. The probability that a region prone to...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - Exercises 33-48 involve probabilities with...Ch. 11.7 - The graph shows that U.S. adults dependent on...Ch. 11.7 - In Exercises 37-42, consider a political...Ch. 11.7 - In Exercises 37-42, consider a political...Ch. 11.7 - In Exercises 43-48, an ice chest contains six cans...Ch. 11.7 - In Exercises 43-48, an ice chest contains six cans...Ch. 11.7 - In Exercises 43-48, an ice chest contains six cans...Ch. 11.7 - In Exercises 43-48, an ice chest contains six cans...Ch. 11.7 - In Exercises 43-48, an ice chest contains six cans...Ch. 11.7 - In Exercises 43-48, an ice chest contains six cans...Ch. 11.7 - Prob. 43ECh. 11.7 - In Exercises 43-48. two tiles are drawn in...Ch. 11.7 - In Exercises 43-48. two tiles are drawn in...Ch. 11.7 - In Exercises 43-48. two tiles are drawn in...Ch. 11.7 - In Exercises 43-48. two tiles are drawn in...Ch. 11.7 - In Exercises 43-48. two tiles are drawn in...Ch. 11.7 - In Exercises 49-52, three tiles are drawn in...Ch. 11.7 - In Exercises 49-52, three tiles are drawn in...Ch. 11.7 - In Exercises 49-52, three tiles are drawn in...Ch. 11.7 - In Exercises 49-52, three tiles are drawn in...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - In Exercises 49-56, the numbered disks shown are...Ch. 11.7 - The table shows the outcome of car accidents in...Ch. 11.7 - The table shows the outcome of car accidents in...Ch. 11.7 - The table shows the outcome of car accidents in...Ch. 11.7 - Find the probability of not wearing a seat belt,...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Shown again is the table indicating the marital...Ch. 11.7 - Prob. 73ECh. 11.7 - In Exercises 49-52, three tiles are drawn in...Ch. 11.7 - Prob. 75ECh. 11.7 - Prob. 76ECh. 11.7 - 73. Probabilities and Coincidence of Shared...Ch. 11.7 - 74. Explain how to find and probabilities with...Ch. 11.7 - Prob. 79ECh. 11.7 - 76. What docs mean? Give an example. Ch. 11.7 - Prob. 81ECh. 11.7 - Prob. 82ECh. 11.7 - Prob. 83ECh. 11.7 - Prob. 84ECh. 11.7 - In Exercises 77-81, write a probability problem...Ch. 11.7 - Make Sense? In Exercises 82-85, determine whether...Ch. 11.7 - Prob. 87ECh. 11.7 - Prob. 88ECh. 11.7 - Make Sense? In Exercises 82-85, determine whether...Ch. 11.7 - 86. If the probability of being hospitalized...Ch. 11.7 - If a single die is rolled five times, what is the...Ch. 11.7 - 88. Nine cards numbered from 1 through 9 are...Ch. 11.7 - If a single die is rolled twice, find the...Ch. 11.8 - CHECK POINT 1 It is equally probable that a...Ch. 11.8 - CHECK POINT 2 A fair coin is tossed four times in...Ch. 11.8 - CHECK POINT 3 Work Example 3 again if the...Ch. 11.8 - CHECK POINT 4 The SAT is a multiple-choice lest....Ch. 11.8 - CHECK POINT 5 A charily is holding a raffle and...Ch. 11.8 - CHECK POINT 6 In the game of one-spot keno, a card...Ch. 11.8 - Fill in each blank so that the resulting statement...Ch. 11.8 - To find the expected value of a game of chance,...Ch. 11.8 - In Exercises 3-4, determine whether each statement...Ch. 11.8 - In Exercises 3-4, determine whether each statement...Ch. 11.8 - In Exercises 1-2, the numbers that each pointer...Ch. 11.8 - In Exercises 1-2, the numbers that each pointer...Ch. 11.8 - The tables in Exercises 3-4 show claims and their...Ch. 11.8 - The tables in Exercises 3-4 show claims and their...Ch. 11.8 - An architect is considering bidding for the design...Ch. 11.8 - A construction company is planning to bid on a...Ch. 11.8 - It is estimated that there are 27 deaths for every...Ch. 11.8 - 8. A 25-year-old can purchase a one-year life...Ch. 11.8 - Exercises 9-10 are related to the SAT, described...Ch. 11.8 - Exercises 9-10 are related to the SAT, described...Ch. 11.8 - 11. A store specializing in mountain bikes is to...Ch. 11.8 - An oil company is considering two sites on which...Ch. 11.8 - 13. In a product liability case, a company can...Ch. 11.8 - A service that repairs air conditioners sells...Ch. 11.8 - Exercises 15-19 involve computing expected values...Ch. 11.8 - Exercises 15-19 involve computing expected values...Ch. 11.8 - Exercises 15-19 involve computing expected values...Ch. 11.8 - Exercises 15-19 involve computing expected values...Ch. 11.8 - Exercises 15-19 involve computing expected values...Ch. 11.8 - What does the expected value for the outcome of...Ch. 11.8 - 21. Explain how to find the expected value for the...Ch. 11.8 - Prob. 22ECh. 11.8 - Prob. 23ECh. 11.8 - Prob. 24ECh. 11.8 - Prob. 25ECh. 11.8 - Make Sense? In Exercises 26-29, determine whether...Ch. 11.8 - Prob. 27ECh. 11.8 - Make Sense? In Exercises 26-29, determine whether...Ch. 11.8 - Make Sense? In Exercises 26-29, determine whether...Ch. 11.8 - A popular state lottery is the 5/35 lottery,...Ch. 11.8 - Refer to the probabilities of dying at any given...Ch. 11 - A restaurant offers 20 appetizers and 40 main...Ch. 11 - A popular brand of pen comes in red, green, blue,...Ch. 11 - In how many ways can first and second prize be...Ch. 11 - 4. You are answering three multiple-choice...Ch. 11 - A stock can go up, go down, or stay unchanged. How...Ch. 11 - A person can purchase a condominium with a choice...Ch. 11 - In Exercises 7-10, evaluate each factorial...Ch. 11 - In Exercises 7-10, evaluate each factorial...Ch. 11 - In Exercises 7-10, evaluate each factorial...Ch. 11 - In Exercises 7-10, evaluate each factorial...Ch. 11 - In Exercises 11-12, use the formula for nPr to...Ch. 11 - In Exercises 11-12, use the formula for n P r to...Ch. 11 - In Exercises 13-14, use the formula for n C r to...Ch. 11 - In Exercises 13-14, use the formula for to...Ch. 11 - In Exercises 15-17, does the problem involve...Ch. 11 - In Exercises 15-17, does the problem involve...Ch. 11 - In Exercises 15-17, does the problem involve...Ch. 11 - In Exercises 18-28, solve each method. Six acts...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - In Exercises 18-28, solve each problem using an...Ch. 11 - Prob. 28RECh. 11 - In Exercises 29-32, a die is rolled. Find the...Ch. 11 - Prob. 30RECh. 11 - Prob. 31RECh. 11 - Prob. 32RECh. 11 - Prob. 33RECh. 11 - Prob. 34RECh. 11 - Prob. 35RECh. 11 - Prob. 36RECh. 11 - Prob. 37RECh. 11 - Prob. 38RECh. 11 - Prob. 39RECh. 11 - Prob. 40RECh. 11 - Prob. 41RECh. 11 - Prob. 42RECh. 11 - Prob. 43RECh. 11 - Prob. 44RECh. 11 - 45. If cities A, B, C, and Dare visited in random...Ch. 11 - Prob. 46RECh. 11 - Prob. 47RECh. 11 - Prob. 48RECh. 11 - Prob. 49RECh. 11 - Prob. 50RECh. 11 - Prob. 51RECh. 11 - If you are dealt 3 cards from a shuffled deck of...Ch. 11 - Prob. 53RECh. 11 - Prob. 54RECh. 11 - Prob. 55RECh. 11 - Prob. 56RECh. 11 - In Exercises 53-57,a die is rolled. Find the...Ch. 11 - Prob. 58RECh. 11 - Prob. 59RECh. 11 - Prob. 60RECh. 11 - Prob. 61RECh. 11 - Prob. 62RECh. 11 - Prob. 63RECh. 11 - In Exercises 64-69, it is equally probable that...Ch. 11 - Prob. 65RECh. 11 - Prob. 66RECh. 11 - Prob. 67RECh. 11 - Prob. 68RECh. 11 - In Exercises 64-69, it is equally probable that...Ch. 11 - Prob. 70RECh. 11 - Use this information to solve Exercises 70-71.At a...Ch. 11 - Prob. 72RECh. 11 - Prob. 73RECh. 11 - Prob. 74RECh. 11 - Prob. 75RECh. 11 - Prob. 76RECh. 11 - Prob. 77RECh. 11 - Prob. 78RECh. 11 - Use the spinner shown to solve Exercises 79-83. It...Ch. 11 - Prob. 80RECh. 11 - Prob. 81RECh. 11 - Prob. 82RECh. 11 - Prob. 83RECh. 11 - Prob. 84RECh. 11 - Prob. 85RECh. 11 - Prob. 86RECh. 11 - Prob. 87RECh. 11 - Prob. 88RECh. 11 - Prob. 89RECh. 11 - 90. A letter is randomly selected from the letters...Ch. 11 - Prob. 91RECh. 11 - Prob. 92RECh. 11 - The data in the table are based on 145 Americans...Ch. 11 - Prob. 94RECh. 11 - Prob. 95RECh. 11 - Prob. 96RECh. 11 - Prob. 97RECh. 11 - The data in the table are based on 145 Americans...Ch. 11 - Prob. 99RECh. 11 - Prob. 100RECh. 11 - Prob. 101RECh. 11 - Prob. 102RECh. 11 - Prob. 103RECh. 11 - In Exercises 100-106, use data in the table to...Ch. 11 - Prob. 105RECh. 11 - Prob. 106RECh. 11 - Prob. 107RECh. 11 - The table shows claims and their probabilities for...Ch. 11 - Prob. 109RECh. 11 - A game is played using a fair coin that is tossed...Ch. 11 - 1. A person can purchase a particular model of a...Ch. 11 - 2. Four acts are scheduled to perform in a variety...Ch. 11 - Prob. 3TCh. 11 - Prob. 4TCh. 11 - Prob. 5TCh. 11 - Prob. 6TCh. 11 - Prob. 7TCh. 11 - Prob. 8TCh. 11 - Prob. 9TCh. 11 - Prob. 10TCh. 11 - Prob. 11TCh. 11 - Prob. 12TCh. 11 - Prob. 13TCh. 11 - Prob. 14TCh. 11 - 15. A region is prone to flooding once every 20...Ch. 11 - Prob. 16TCh. 11 - Prob. 17TCh. 11 - Prob. 18TCh. 11 - Prob. 19TCh. 11 - Prob. 20TCh. 11 - Prob. 21TCh. 11 - Prob. 22TCh. 11 - Prob. 23TCh. 11 - Prob. 24TCh. 11 - Prob. 25TCh. 11 - Prob. 26TCh. 11 - Prob. 27TCh. 11 - Prob. 28T

Additional Math Textbook Solutions

Find more solutions based on key concepts
In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...

Elementary Statistics (13th Edition)

For Problems 23-28, write in simpler form, as in Example 4. logbFG

Finite Mathematics for Business, Economics, Life Sciences and Social Sciences

1. How much money is Joe earning when he’s 30?

Pathways To Math Literacy (looseleaf)

Is there a relationship between wine consumption and deaths from heart disease? The table gives data from 19 de...

College Algebra Essentials (5th Edition)

1. How is a sample related to a population?

Elementary Statistics: Picturing the World (7th Edition)

The largest polynomial that divides evenly into a list of polynomials is called the _______.

Elementary & Intermediate Algebra

Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License