
Interpretation:
To write the program to compute the
Concept Introduction:
An attractor that come out in a simplified system of equations which describes two-dimensional fluid flow of uniform depth is known as Lorenz attractor.
It is a system of ordinary differential equation.
Answer to Problem 1E
Solution:
The Matlab program is written to compute the correlation dimension of the Lorenz attractor.
The slope of the second figure depends on the value of correlation; hence, the dimension depends on r.
Explanation of Solution
Using Matlab, we can write a program to compute the correlation dimension of the Lorenz attractor.
By running the above Matlab code, we get the Lorenz attractor correlation as below:
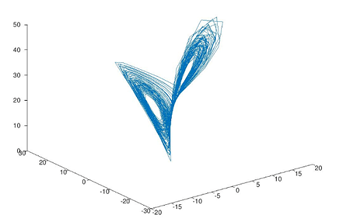
This is the correlation dimension of Lorenz attractor.
Now consider the slope to be
Now use the below Matlab code to reproduce the figure
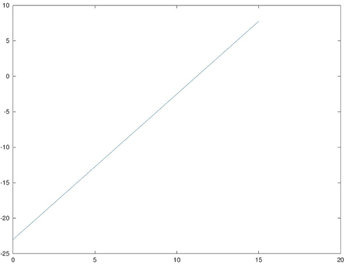
Hence, this is the required curve.
The slope of the above figure depends on the value of correlation; hence, the dimension depends on r.
The correlation dimension of the Lorenz attractor is computed. The slope of the figure depends on the value of correlation; hence, dimension depends on r.
Want to see more full solutions like this?
Chapter 11 Solutions
Nonlinear Dynamics and Chaos
- Find the general solution of the given system. 6 -(-1)x x' = -6 11 x(t) = x(t) = e5t)*[(c1 + c2(t− 1/6))(c1 + c2t)] Your answer cannoarrow_forward(c) Describe the distribution plan and show the total distribution cost. Optimal Solution Amount Cost $ 2000 Southern-Hamilton 200 Southern-Butler $ Southern-Clermont 300 4500 Northwest-Hamilton 200 $2400 Northwest-Butler 200 $3000 Northwest-Clermont $ Total Cost ક (d) Recent residential and industrial growth in Butler County has the potential for increasing demand by 100 units. (i) Create an updated distribution plan assuming Southern Gas becomes the preferred supplier. Distribution Plan with Southern Gas Amount Southern-Hamilton $ Cost × Southern-Butler x $ Southern-Clermont 300 $ 4500 Northwest-Hamilton 64 x Northwest-Butler $ × Northwest-Clermont 0 $0 Total Cost $ (ii) Create an updated distribution plan assuming Northwest Gas becomes the preferred supplier. Distribution Plan with Northwest Gas Southern-Hamilton Southern-Butler 0 Southern-Clermont Northwest-Hamilton Northwest-Butler Northwest-Clermont Total Cost Amount × x x +7 $0 Cost × $ × $ × +4 $ -/+ $ × ×arrow_forwardThe distribution system for the Herman Company consists of three plants, two warehouses, and four customers. Plant capacities and shipping costs per unit (in $) from each plant to each warehouse are as follows. Warehouse Plant Capacity 1 2 1 4 7 450 2 8 5 600 3 5 6 380 Customer demand and shipping costs per unit (in $) from each warehouse to each customer are as follows. Customer Warehouse 1 2 3 1 6 4 8 2 3 6 7 7 Demand 300 300 300 400 (a) Develop a network representation of this problem. (Submit a file with a maximum size of 1 MB.) Choose File No file chosen This answer has not been graded yet. (b) Formulate a linear programming model of the problem. (Let Plant 1 be node 1, Plant 2 be node 2, Plant 3 be node 3, Warehouse 1 be node 4, Warehouse 2 be node 5, Customer 1 be node 6, Customer 2 be node 7, Customer 3 be node 8, and Customer 4 be node 9. Express your answers in the form x;;, where x,; represents the number of units shipped from node i to node j.) Min 4x14+8x24+5x34+7x15 +5x25…arrow_forward
- A linear programming computer package is needed. Hanson Inn is a 96-room hotel located near the airport and convention center in Louisville, Kentucky. When a convention or a special event is in town, Hanson increases its normal room rates and takes reservations based on a revenue management system. A large profesional organization has scheduled its annual convention in Louisville for the first weekend in June. Hanson Inn agreed to make at least 50% of its rooms available for convention attendees at a special convention rate in order to be listed as a recommended hotel for the convention. Although the majority of attendees at the annual meeting typically request a Friday and Saturday two-night package, some attendees may select a Friday night only or a Saturday night only reservation. Customers not attending the convention may also request a Friday and Saturday two-night package, or make a Friday night only or Saturday night only reservation. Thus, six types of reservations are…arrow_forward25.2. Find the Laurent series for the function 1/[z(z-1)] in the follow- ing domains: (a). 0<|z|< 1, (b). 1<|z, (c). 0arrow_forward25.5. Find the Laurent series for the function 1/[(z - 1)(-2)(z - 3)] in the following domains: (a). 0 3. شهریarrow_forward25.1. Expand each of the following functions f(z) in a Laurent series on the indicated domain: (a). z² - 2z+5 (2-2)(z² + 1)' (c). Log za 2 b (z - موجود 11, 29, where b>a> 1 are real, |z| > b.arrow_forward25.3. Find the Laurent series for the function z/[(22 + 1)(z² + 4)] in the following domains (a). 02.arrow_forward25.2. Find the Laurent series for the function 1/[z(z-1)] in the follow- ing domains: (a). 0<|z|< 1, (b). 1 <|z|, (c). 0<|z1|< 1, (d). 1< |z1|, (e). 1<|z2|<2.arrow_forward25.1. Expand each of the following functions f(z) in a Laurent series on the indicated domain: 22-2z+5 (z - 2) (z² + 1)' (z 11, 22 (a). (c). Log (2-8) where b>a> 1 are real, |z|> b. barrow_forward25.5. Find the Laurent series for the function 1/[(2-1)(z-2)(z-3)] in the following domains: (a). 0 3.arrow_forwardCan you explain how the error term in the CF Algorithm relates to the (m+1)th complete quotient? Also, what would be a good way to explain the connection between these two slides? How can one transition between them for a presentation?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

