
Interpretation:
To write the program to compute the
Concept Introduction:
An attractor that come out in a simplified system of equations which describes two-dimensional fluid flow of uniform depth is known as Lorenz attractor.
It is a system of ordinary differential equation.
Answer to Problem 1E
Solution:
The Matlab program is written to compute the correlation dimension of the Lorenz attractor.
The slope of the second figure depends on the value of correlation; hence, the dimension depends on r.
Explanation of Solution
Using Matlab, we can write a program to compute the correlation dimension of the Lorenz attractor.
By running the above Matlab code, we get the Lorenz attractor correlation as below:
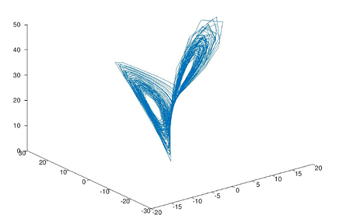
This is the correlation dimension of Lorenz attractor.
Now consider the slope to be
Now use the below Matlab code to reproduce the figure

Hence, this is the required curve.
The slope of the above figure depends on the value of correlation; hence, the dimension depends on r.
The correlation dimension of the Lorenz attractor is computed. The slope of the figure depends on the value of correlation; hence, dimension depends on r.
Want to see more full solutions like this?
Chapter 11 Solutions
EBK NONLINEAR DYNAMICS AND CHAOS WITH S
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Complete solution requiredarrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Do on pen and paper onlyarrow_forwardProblem 9: The 30-kg pipe is supported at A by a system of five cords. Determine the force in each cord for equilibrium. B 60º A E Harrow_forwardd((x, y), (z, w)) = |xz|+|yw|, show that whether d is a metric on R² or not?. Q3/Let R be a set of real number and d: R² x R² → R such that -> d((x, y), (z, w)) = max{\x - zl, ly - w} show that whether d is a metric on R² or not?. Q4/Let X be a nonempty set and d₁, d₂: XXR are metrics on X let d3,d4, d5: XX → R such that d3(x, y) = 4d2(x, y) d4(x, y) = 3d₁(x, y) +2d2(x, y) d5(x,y) = 2d₁ (x,y))/ 1+ 2d₂(x, y). Show that whether d3, d4 and d5 are metric on X or not?arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

