Chapter 11.4, Problem 90AYU

In graph theory, an adjacency matrix, A, is a way of representing which nodes (or vertices) are connected. For a simple directed graph, each entry, , is either 1 (if a direct path exists from node i to node j) or 0 (if no direct path exists from node i to node j). For example, consider the following graph and corresponding adjacency matrix. 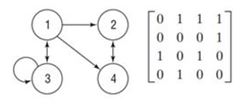The entry is 1 because a direct path exists from node 1 to node 4. However, the entry is 0 because no path exists from node 4 to node 1. The entry is 1 because a direct path exists from node 3 to itself. The matrix indicates the number of ways to get from node i to node j within k moves (steps).

Website Map A content map can be used to show how different pages on a website are connected. For example, the following content map shows the relationship among the five pages of a certain website with links between pages represented by arrows. 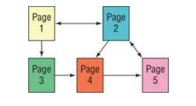The content map can be represented by a 5 by 5 adjacency matrix where each entry, $a_{ij}$, is either 1 (if a link exists from page i to page j) or 0 (if no link exists from page i to page j).

(a) Write the 5 by 5 adjacency matrix that represents the given content map.

(b) Explain the significance of the entries on the main diagonal in your result from part (a).

(c) Find and interpret $A^2$.