
Concept explainers
a.
To find: a formula for the instantaneous rate of change of the balloon.
a.
Answer to Problem 71E
Explanation of Solution
Given information: A water balloon is thrown upward from the top of an 80-foot
building with an initial velocity of 64 feet per second. The height or displacement s (in feet) of the balloon can be modeled by the position function
Calculation:
b.
To find: the average rate of change of the balloon after the first three second of flight.
b.
Answer to Problem 71E
Explanation of Solution
Given information:
Calculation:
c.
To find: the time at which the balloon reaches its maximum height.
c.
Answer to Problem 71E
The time at which the balloon reaches its maximum height is 2 seconds.
Explanation of Solution
Given information:
Calculation:
d.
To find: the velocity of the balloon as it impacts the ground.
d.
Answer to Problem 71E
The velocity of the balloon as it impacts the ground is -96 ft/sec.
Explanation of Solution
Given information:
Calculation:
e.
To graph: the model using a graphing utility.
e.
Explanation of Solution
Given information:
Calculation:
The graph of the model using the graphing utility is shown below.
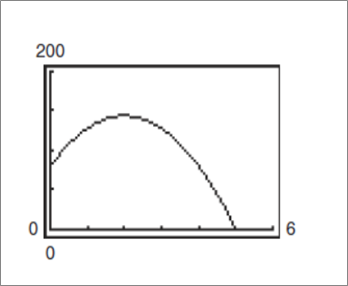
Chapter 11 Solutions
PRECALCULUS W/LIMITS:GRAPH.APPROACH(HS)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





