
(i)
To graph: A cluster bar graph showing the percentages of Congress members from each party who spent each designated amount in their respective home districts.
(i)
Explanation of Solution
Calculation: To find the percentage table:
| Party | Less than 5 Billion | 5 to 10 Billion | More than 10 Billion |
| Democratic | |||
| Republican |
Graph: To create cluster bar graph by using Excel is as follows:
Step 1: Enter the percentage data table in Excel worksheet.
Step 2: Select table and go to Insert > Charts > Column.
The cluster bar graph is obtained as:
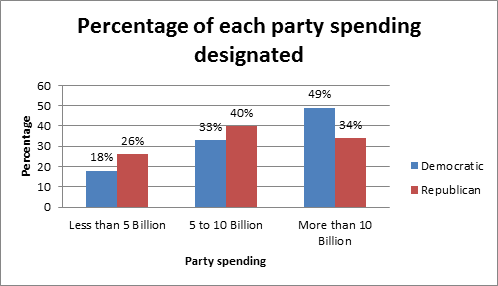
(ii)
(a)
The level of significance and state the null and alternative hypotheses.
(ii)
(a)
Answer to Problem 18P
Solution: The level of significance is 0.01.
Explanation of Solution
The level of significance,
The null hypothesis for testing is defined as,
The alternative hypothesis is defined as,
(b)
To test: Whether all the expected frequencies are greater than 5. Also determine the value of chi-square statistic for the sample, the sampling distribution that should be used and degrees of freedom for the test.
(b)
Answer to Problem 18P
Solution: The value of chi-square statistic for the sample,
Explanation of Solution
Calculation: The find the
Step 1: Go to Stat >Tables> Chi-square Test For Association.
Step 2: Select ‘Summarized data in two-way table’ and select <5B, 5-10B, >10Bin ‘Columns containing the table’ box.
Step 3: Select ‘Partyin ‘Rows’ and write any name in ‘Columns’ and click on ‘Statistics’ tick on Chi-square test and Expected cell counts. Then click on OK.
The Minitab output is:
Chi-Square Test for Association: Party, spent
Rows: Party Columns: spent
| <5B | 5-10B | >10B | |
| Democratic | 9.78 | 16.63 | 18.59 |
| Republican | 10.22 | 17.37 | 19.41 |
Cell Contents
Expected count
Chi-Square Test
| Chi-Square | DF | P-Value | |
| Pearson | 2.176 | 2 | 0.337 |
| Likelihood Ratio | 2.185 | 2 | 0.335 |
Therefore, the obtained Chi-square test statistics is 2.176.
The obtained expected frequencies are:
| Party | <5B | 5-10B | >10B |
| Democratic | 9.78 | 16.63 | 18.59 |
| Republican | 10.22 | 17.37 | 19.41 |
So, all expected frequencies are greater than 5.
The chi-square distribution should be used in this study and the obtained degrees of freedom are 2.
(c)
The P-value of the sample statistic.
(c)
Answer to Problem 18P
Solution: The P-value of sample statistic is 0.337.
Explanation of Solution
Calculation: The Minitab output obtained in above part (b) also gives the P-value. So, the P-value for the sample test statistic is 0.337.
(d)
To explain: Whether we will reject or fails to reject the null hypothesis.
(d)
Answer to Problem 18P
Solution: We failed to reject the null hypothesis at significance level 0.05.
Explanation of Solution
The obtained results in part (a), (b) and (c) are,
Since the P-value (0.337) is greater than 0.01, hence we failed to reject the null hypothesis of independence at
(e)
To explain: The conclusion in the context of application.
(e)
Answer to Problem 18P
Solution: It is concluded that the Stone tools construction material and sitearenot independent.
Explanation of Solution
From above part, it can be seen that we failed to reject the null hypothesis at
Therefore, at the 1% level of significance, there is sufficient evidence to conclude that congressional members of each political party spent designated amounts in the same proportions.
Want to see more full solutions like this?
Chapter 11 Solutions
Bundle: Understanding Basic Statistics, Loose-leaf Version, 7th + WebAssign Printed Access Card for Brase/Brase's Understanding Basic Statistics, ... for Peck's Statistics: Learning from Data
- The table available below shows the costs per mile (in cents) for a sample of automobiles. At a = 0.05, can you conclude that at least one mean cost per mile is different from the others? Click on the icon to view the data table. Let Hss, HMS, HLS, Hsuv and Hмy represent the mean costs per mile for small sedans, medium sedans, large sedans, SUV 4WDs, and minivans respectively. What are the hypotheses for this test? OA. Ho: Not all the means are equal. Ha Hss HMS HLS HSUV HMV B. Ho Hss HMS HLS HSUV = μMV Ha: Hss *HMS *HLS*HSUV * HMV C. Ho Hss HMS HLS HSUV =μMV = = H: Not all the means are equal. D. Ho Hss HMS HLS HSUV HMV Ha Hss HMS HLS =HSUV = HMVarrow_forwardQuestion: A company launches two different marketing campaigns to promote the same product in two different regions. After one month, the company collects the sales data (in units sold) from both regions to compare the effectiveness of the campaigns. The company wants to determine whether there is a significant difference in the mean sales between the two regions. Perform a two sample T-test You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. (2 points = 0.5 x 4 Answers) Each of these is worth 0.5 points. However, showing the calculation is must. If calculation is missing, the whole answer won't get any credit.arrow_forwardBinomial Prob. Question: A new teaching method claims to improve student engagement. A survey reveals that 60% of students find this method engaging. If 15 students are randomly selected, what is the probability that: a) Exactly 9 students find the method engaging?b) At least 7 students find the method engaging? (2 points = 1 x 2 answers) Provide answers in the yellow cellsarrow_forward
- In a survey of 2273 adults, 739 say they believe in UFOS. Construct a 95% confidence interval for the population proportion of adults who believe in UFOs. A 95% confidence interval for the population proportion is ( ☐, ☐ ). (Round to three decimal places as needed.)arrow_forwardFind the minimum sample size n needed to estimate μ for the given values of c, σ, and E. C=0.98, σ 6.7, and E = 2 Assume that a preliminary sample has at least 30 members. n = (Round up to the nearest whole number.)arrow_forwardIn a survey of 2193 adults in a recent year, 1233 say they have made a New Year's resolution. Construct 90% and 95% confidence intervals for the population proportion. Interpret the results and compare the widths of the confidence intervals. The 90% confidence interval for the population proportion p is (Round to three decimal places as needed.) J.D) .arrow_forward
- Let p be the population proportion for the following condition. Find the point estimates for p and q. In a survey of 1143 adults from country A, 317 said that they were not confident that the food they eat in country A is safe. The point estimate for p, p, is (Round to three decimal places as needed.) ...arrow_forward(c) Because logistic regression predicts probabilities of outcomes, observations used to build a logistic regression model need not be independent. A. false: all observations must be independent B. true C. false: only observations with the same outcome need to be independent I ANSWERED: A. false: all observations must be independent. (This was marked wrong but I have no idea why. Isn't this a basic assumption of logistic regression)arrow_forwardBusiness discussarrow_forward
- Spam filters are built on principles similar to those used in logistic regression. We fit a probability that each message is spam or not spam. We have several variables for each email. Here are a few: to_multiple=1 if there are multiple recipients, winner=1 if the word 'winner' appears in the subject line, format=1 if the email is poorly formatted, re_subj=1 if "re" appears in the subject line. A logistic model was fit to a dataset with the following output: Estimate SE Z Pr(>|Z|) (Intercept) -0.8161 0.086 -9.4895 0 to_multiple -2.5651 0.3052 -8.4047 0 winner 1.5801 0.3156 5.0067 0 format -0.1528 0.1136 -1.3451 0.1786 re_subj -2.8401 0.363 -7.824 0 (a) Write down the model using the coefficients from the model fit.log_odds(spam) = -0.8161 + -2.5651 + to_multiple + 1.5801 winner + -0.1528 format + -2.8401 re_subj(b) Suppose we have an observation where to_multiple=0, winner=1, format=0, and re_subj=0. What is the predicted probability that this message is spam?…arrow_forwardConsider an event X comprised of three outcomes whose probabilities are 9/18, 1/18,and 6/18. Compute the probability of the complement of the event. Question content area bottom Part 1 A.1/2 B.2/18 C.16/18 D.16/3arrow_forwardJohn and Mike were offered mints. What is the probability that at least John or Mike would respond favorably? (Hint: Use the classical definition.) Question content area bottom Part 1 A.1/2 B.3/4 C.1/8 D.3/8arrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill


