Elementary Linear Algebra: Applications Version
12th Edition
ISBN: 9781119282365
Author: Howard Anton, Chris Rorres, Anton Kaul
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 1.10, Problem 5E
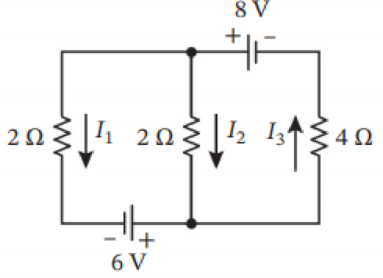
In Exercises 5–8, analyze the given electrical circuits by finding the unknown currents.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
How long is a guy wire reaching from the top of a
15-foot pole to a point on the ground
9-feet from the pole?
Question content area bottom
Part 1
The guy wire is exactly
feet long.
(Type an exact answer, using radicals as needed.)
Part 2
The guy wire is approximatelyfeet long.
(Round to the nearest thousandth.)
Question 6
Not yet
answered
Marked out of
5.00
Flag question
=
If (4,6,-11) and (-12,-16,4),
=
Compute the cross product vx w
k
Consider the following vector field v^-> (x,y):
v^->(x,y)=2yi−xj
What is the magnitude of the vector v⃗ located in point (13,9)?
[Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places]
Chapter 1 Solutions
Elementary Linear Algebra: Applications Version
Ch. 1.1 - In each part, determine whether the equation is...Ch. 1.1 - In each part, determine whether the equation is...Ch. 1.1 - Using the notation of Formula (7), write down a...Ch. 1.1 - Write down the augmented matrix for each of the...Ch. 1.1 - In each part of Exercises 56, find a system of...Ch. 1.1 - In each part of Exercises 56, find a system of...Ch. 1.1 - In each part of Exercises 78, find the augmented...Ch. 1.1 - In each part of Exercises 78, find the augmented...Ch. 1.1 - In each part, determine whether the given 3-tuple...Ch. 1.1 - In each part, determine whether the given 3-tuple...
Ch. 1.1 - In each part, solve the linear system, if...Ch. 1.1 - Under what conditions on a and b will the linear...Ch. 1.1 - In each part of Exercises 1314, use parametric...Ch. 1.1 - In each part of Exercises 1314, use parametric...Ch. 1.1 - In Exercises 1516, each linear system has...Ch. 1.1 - In Exercises 1516, each linear system has...Ch. 1.1 - In Exercises 1718, find a single elementary row...Ch. 1.1 - In Exercises 1718, find a single elementary row...Ch. 1.1 - In Exercises 1920, find all values of k for which...Ch. 1.1 - In Exercises 1920, find all values of k for which...Ch. 1.1 - The curve y=ax2+bx+c shown in the accompanying...Ch. 1.1 - Explain why each of the three elementary row...Ch. 1.1 - Show that if the linear equations x1+kx2=c and...Ch. 1.1 - Consider the system of equations...Ch. 1.1 - Suppose that a certain diet calls for 7 units of...Ch. 1.1 - Suppose that you want to find values for a, b, and...Ch. 1.1 - Suppose you are asked to find three real numbers...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - In parts (a)(h) determine whether the statement is...Ch. 1.1 - Use the result in Exercise 21 to find values of a,...Ch. 1.2 - In Exercises 12, determine whether the matrix is...Ch. 1.2 - In Exercises 12, determine whether the matrix is...Ch. 1.2 - In Exercises 34, suppose that the augmented matrix...Ch. 1.2 - In Exercises 34, suppose that the augmented matrix...Ch. 1.2 - In Exercises 58, solve the system by Gaussian...Ch. 1.2 - In Exercises 58, solve the system by Gaussian...Ch. 1.2 - In Exercises 58, solve the system by Gaussian...Ch. 1.2 - In Exercises 58, solve the system by Gaussian...Ch. 1.2 - In Exercises 912, solve the system by GaussJordan...Ch. 1.2 - In Exercises 912, solve the system by GaussJordan...Ch. 1.2 - In Exercises 912, solve the system by GaussJordan...Ch. 1.2 - In Exercises 912, solve the system by GaussJordan...Ch. 1.2 - In Exercises 1314, determine whether the...Ch. 1.2 - In Exercises 1314, determine whether the...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In Exercises 1522, solve the given linear system...Ch. 1.2 - In each part of Exercises 2324, the augmented...Ch. 1.2 - In each part of Exercises 2324, the augmented...Ch. 1.2 - In Exercises 2526, determine the values of a for...Ch. 1.2 - In Exercises 2526, determine the values of a for...Ch. 1.2 - In Exercises 2728, what condition, if any, must a,...Ch. 1.2 - In Exercises 2728, what condition, if any, must a,...Ch. 1.2 - In Exercises 2930, solve the following systems,...Ch. 1.2 - In Exercises 2930, solve the following systems,...Ch. 1.2 - Find two different row echelon forms of [1327]...Ch. 1.2 - Reduce [2130229345] to reduced row echelon form...Ch. 1.2 - Show that the following nonlinear system has 18...Ch. 1.2 - Solve the following system of nonlinear equations...Ch. 1.2 - Solve the following system of nonlinear equations...Ch. 1.2 - Solve the following system for x, y, and z....Ch. 1.2 - Find the coefficients a, b, c, and d so that the...Ch. 1.2 - Prob. 38ECh. 1.2 - If the linear system...Ch. 1.2 - a. If A is a matrix with three rows and five...Ch. 1.2 - Describe all possible reduced row echelon forms of...Ch. 1.2 - Consider the system of equations...Ch. 1.2 - a. Prove that if adbc0, then the reduced row...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - In parts (a)(i) determine whether the statement is...Ch. 1.2 - Find the reduced row echelon form of the augmented...Ch. 1.2 - Find values of the constants A, B, C, and D that...Ch. 1.3 - In Exercises 12, suppose that A, B, C, D, and E...Ch. 1.3 - In Exercises 12, suppose that A, B, C, D, and E...Ch. 1.3 - In Exercises 36, use the following matrices to...Ch. 1.3 - In Exercises 36, use the following matrices to...Ch. 1.3 - In Exercises 36, use the following matrices to...Ch. 1.3 - In Exercises 36, use the following matrices to...Ch. 1.3 - In Exercises 78, use the following matrices and...Ch. 1.3 - In Exercises 78, use the following matrices and...Ch. 1.3 - In Exercises 910, use matrices A and B from...Ch. 1.3 - In Exercises 910, use matrices A and B from...Ch. 1.3 - In each part of Exercises 1112, find matrices A,...Ch. 1.3 - In each part of Exercises 1112, find matrices A,...Ch. 1.3 - In each part of Exercises 1314, express the matrix...Ch. 1.3 - In each part of Exercises 1314, express the matrix...Ch. 1.3 - In Exercises 1516, find all values of k, if any,...Ch. 1.3 - In Exercises 1516, find all values of k, if any,...Ch. 1.3 - In Exercises 1720, use the column-row expansion of...Ch. 1.3 - In Exercises 1720, use the column-row expansion of...Ch. 1.3 - In Exercises 1720, use the column-row expansion of...Ch. 1.3 - In Exercises 1720, use the column-row expansion of...Ch. 1.3 - For the linear system in Example 5 of Section 1.2,...Ch. 1.3 - Follow the directions of Exercise 21 for the...Ch. 1.3 - In Exercises 2324, solve the matrix equation for...Ch. 1.3 - In Exercises 23 24, solve the matrix equation for...Ch. 1.3 - a. Show that if A has a row of zeros and B is any...Ch. 1.3 - In each part, find a 6 6 matrix [aij] that...Ch. 1.3 - In Exercises 2728, how many 3 3 matrices A can...Ch. 1.3 - In Exercises 2728, how many 3 3 matrices A can...Ch. 1.3 - A matrix B is said to be a square root of a matrix...Ch. 1.3 - Let 0 denote a 2 2 matrix, each of whose entries...Ch. 1.3 - Establish Formula (11) by using Formula (5) to...Ch. 1.3 - Find a 4 4 matrix A = [aij] whose entries satisfy...Ch. 1.3 - Suppose that type I items cost 1 each, type II...Ch. 1.3 - The accompanying table shows a record of May and...Ch. 1.3 - Prove: If A and B are n n matrices, then...Ch. 1.3 - a. Prove: If AB and BA are both defined, then AB...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.3 - In parts (a)(o) determine whether the statement is...Ch. 1.4 - In Exercises 12, verify that the following...Ch. 1.4 - In Exercises 12, verify that the following...Ch. 1.4 - In Exercises 34, verify that the matrices and...Ch. 1.4 - In Exercises 34, verify that the matrices and...Ch. 1.4 - In Exercises 58, use Theorem 1.4.5 to compute the...Ch. 1.4 - In Exercises 58, use Theorem 1.4.5 to compute the...Ch. 1.4 - In Exercises 58, use Theorem 1.4.5 to compute the...Ch. 1.4 - In Exercises 58, use Theorem 1.4.5 to compute the...Ch. 1.4 - Find the inverse of...Ch. 1.4 - Find the inverse of [cossinsincos]Ch. 1.4 - In Exercises 1114, verify that the equations are...Ch. 1.4 - In Exercises 1114, verify that the equations are...Ch. 1.4 - In Exercises 1114, verify that the equations are...Ch. 1.4 - In Exercises 1114, verify that the equations are...Ch. 1.4 - In Exercises 1518, use the given information to...Ch. 1.4 - In Exercises 1518, use the given information to...Ch. 1.4 - In Exercises 1518, use the given information to...Ch. 1.4 - In Exercises 1518, use the given information to...Ch. 1.4 - In Exercises 1920, compute the following using the...Ch. 1.4 - In Exercises 1920, compute the following using the...Ch. 1.4 - In Exercises 2122, compute p(A) for the given...Ch. 1.4 - In Exercises 2122, compute p(A) for the given...Ch. 1.4 - In Exercises 2324, let A=[abcd], B=[0100],...Ch. 1.4 - In Exercises 2324, let A=[abcd], B=[0100],...Ch. 1.4 - In Exercises 2528, use the method of Example 8 to...Ch. 1.4 - In Exercises 2528, use the method of Example 8 to...Ch. 1.4 - In Exercises 2528, use the method of Example 8 to...Ch. 1.4 - In Exercises 2528, use the method of Example 8 to...Ch. 1.4 - If a polynomial p(x) can be factored as a product...Ch. 1.4 - If a polynomial p(x) can be factored as a product...Ch. 1.4 - a. Give an example of two 2 2 matrices such that...Ch. 1.4 - The numerical equation a2 = 1 has exactly two...Ch. 1.4 - a. Show that if a square matrix A satisfies the...Ch. 1.4 - Is it possible for A3 to be an identity matrix...Ch. 1.4 - Can a matrix with a row of zeros or a column of...Ch. 1.4 - Can a matrix with two identical rows or two...Ch. 1.4 - In Exercises 3738, determine whether A is...Ch. 1.4 - In Exercises 3738, determine whether A is...Ch. 1.4 - In Exercises 3940, simplify the expression...Ch. 1.4 - In Exercises 3940, simplify the expression...Ch. 1.4 - Show that if R is a 1 n matrix and C is an n 1...Ch. 1.4 - If A is a square matrix and n is a positive...Ch. 1.4 - a. Show that if A is invertible and AB = AC, then...Ch. 1.4 - Show that if A is invertible and k is any nonzero...Ch. 1.4 - a. Show that if A, B, and A + B are invertible...Ch. 1.4 - A square matrix A is said to be idempotent if A2 =...Ch. 1.4 - Show that if A is a square matrix such that Ak = 0...Ch. 1.4 - Show that the matrix A=[abcd] satisfies the...Ch. 1.4 - Assuming that all matrices are n n and...Ch. 1.4 - Assuming that all matrices are n n and...Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In Exercises 5158, prove the stated result....Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.4 - In parts (a)(k) determine whether the statement is...Ch. 1.5 - In Exercises 12, determine whether the given...Ch. 1.5 - In Exercises 12, determine whether the given...Ch. 1.5 - In Exercises 34, find a row operation and the...Ch. 1.5 - In Exercises 34, find a row operation and the...Ch. 1.5 - In Exercises 56 an elementary matrix E and a...Ch. 1.5 - In Exercises 56 an elementary matrix E and a...Ch. 1.5 - In Exercises 78, use the following matrices and...Ch. 1.5 - In Exercises 78, use the following matrices and...Ch. 1.5 - In Exercises 910, first use Theorem 1.4.5 and then...Ch. 1.5 - In Exercises 910, first use Theorem 1.4.5 and then...Ch. 1.5 - In Exercises 1112, use the inversion algorithm to...Ch. 1.5 - In Exercises 1112, use the inversion algorithm to...Ch. 1.5 - In Exercises 1318, use the inversion algorithm to...Ch. 1.5 - In Exercises 1318, use the inversion algorithm to...Ch. 1.5 - In Exercises 1318, use the inversion algorithm to...Ch. 1.5 - In Exercises 1318, use the inversion algorithm to...Ch. 1.5 - In Exercises 1318, use the inversion algorithm to...Ch. 1.5 - In Exercises 1318, use the inversion algorithm to...Ch. 1.5 - In Exercises 1920, find the inverse of each of the...Ch. 1.5 - In Exercises 1920, find the inverse of each of the...Ch. 1.5 - In Exercises 2122, find all values of c, if any,...Ch. 1.5 - In Exercises 2122, find all values of c, if any,...Ch. 1.5 - In Exercises 2326, express the matrix and its...Ch. 1.5 - In Exercises 2326, express the matrix and its...Ch. 1.5 - In Exercises 2326, express the matrix and its...Ch. 1.5 - In Exercises 2326, express the matrix and its...Ch. 1.5 - In Exercises 2728, show that the matrices A and B...Ch. 1.5 - In Exercises 2728, show that the matrices A and B...Ch. 1.5 - Show that if A=[100010abc] is an elementary...Ch. 1.5 - Show that A=[0a000b0c000d0e000f0g000h0] is not...Ch. 1.5 - Prove that if A and B are m n matrices, then A...Ch. 1.5 - Prove that if A is an invertible matrix and B is...Ch. 1.5 - Prove that if B is obtained from A by performing a...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.5 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 18, solve the system by inverting the...Ch. 1.6 - In Exercises 912, solve the linear systems. Using...Ch. 1.6 - In Exercises 912, solve the linear systems. Using...Ch. 1.6 - In Exercises 912, solve the linear systems. Using...Ch. 1.6 - In Exercises 912, solve the linear systems. Using...Ch. 1.6 - In Exercises 1317, determine conditions on the...Ch. 1.6 - In Exercises 1317, determine conditions on the...Ch. 1.6 - In Exercises 1317, determine conditions on the...Ch. 1.6 - In Exercises 1317, determine conditions on the...Ch. 1.6 - In Exercises 1317, determine conditions on the...Ch. 1.6 - Consider the matrices A=[212222311] and x=[x1x2x3]...Ch. 1.6 - In Exercises 1920, solve the matrix equation for...Ch. 1.6 - In Exercises 1920, solve the matrix equation for...Ch. 1.6 - Let Ax = 0 be a homogeneous system of n linear...Ch. 1.6 - Let Ax = 0 be a homogeneous system of n linear...Ch. 1.6 - Let Ax = b be any consistent system of linear...Ch. 1.6 - Use part (a) of Theorem 1.6.3 to prove part (b)....Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - In parts (a)(g) determine whether the statement is...Ch. 1.6 - Colors in print media, on computer monitors, and...Ch. 1.6 - Let A=[122451031], B1=[017], B2=[1153], B3=[142]...Ch. 1.7 - In Exercises 12, classify the matrix as upper...Ch. 1.7 - In Exercises 12, classify the matrix as upper...Ch. 1.7 - In Exercises 36, find the product by inspection....Ch. 1.7 - In Exercises 36, find the product by inspection....Ch. 1.7 - In Exercises 36, find the product by inspection....Ch. 1.7 - In Exercises 36, find the product by inspection....Ch. 1.7 - In Exercises 710, find A, A2, and Ak (where k is...Ch. 1.7 - In Exercises 710, find A2, A2, and Ak (where k is...Ch. 1.7 - In Exercises 710, find A2, A2, and Ak (where k is...Ch. 1.7 - In Exercises 710, find A2, A2, and Ak (where k is...Ch. 1.7 - In Exercises 1112, compute the product by...Ch. 1.7 - In Exercises 1112, compute the product by...Ch. 1.7 - In Exercises 1314, compute the indicated quantity....Ch. 1.7 - In Exercises 1314, compute the indicated quantity...Ch. 1.7 - In Exercises 1516, use what you have learned in...Ch. 1.7 - In Exercises 1516, use what you have learned in...Ch. 1.7 - In Exercises 1718, create a symmetric matrix by...Ch. 1.7 - In Exercises 1718, create a symmetric matrix by...Ch. 1.7 - In Exercises 1922, determine by inspection whether...Ch. 1.7 - In Exercises 1922, determine by inspection whether...Ch. 1.7 - In Exercises 1922, determine by inspection whether...Ch. 1.7 - In Exercises 1922, determine by inspection whether...Ch. 1.7 - In Exercises 2324, find the diagonal entries of AB...Ch. 1.7 - In Exercises 2324, find the diagonal entries of AB...Ch. 1.7 - In Exercises 2526, find all values of the unknown...Ch. 1.7 - In Exercises 2526, find all values of the unknown...Ch. 1.7 - In Exercises 2728, find all values of x for which...Ch. 1.7 - In Exercises 2728, find all values of x for which...Ch. 1.7 - If A is an invertible upper triangular or lower...Ch. 1.7 - Show that if A is a symmetric n n matrix and B is...Ch. 1.7 - In Exercises 3132, find a diagonal matrix A that...Ch. 1.7 - In Exercises 3132, find a diagonal matrix A that...Ch. 1.7 - Verify Theorem 1.7.1(b) for the matrix product AB...Ch. 1.7 - Let A be an n n symmetric matrix. a. Show that A2...Ch. 1.7 - Verify Theorem 1.7.4 for the given matrix A. a....Ch. 1.7 - Find all 3 3 diagonal matrices A that satisfy...Ch. 1.7 - Let A = [aij] be an n n matrix. Determine whether...Ch. 1.7 - On the basis of your experience with Exercise 37,...Ch. 1.7 - Find an upper triangular matrix that satisfies...Ch. 1.7 - If the n n matrix A can be expressed as A = LU,...Ch. 1.7 - In the text we defined a matrix A to be symmetric...Ch. 1.7 - In the text we defined a matrix A to be symmetric...Ch. 1.7 - In the text we defined a matrix A to be symmetric...Ch. 1.7 - In the text we defined a matrix A to be symmetric...Ch. 1.7 - In the text we defined a matrix A to be symmetric...Ch. 1.7 - Prove: If the matrices A and B are both upper...Ch. 1.7 - Prove: If ATA = A, then A is symmetric and A = A2.Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.7 - In parts (a)(m) determine whether the statement is...Ch. 1.8 - In Exercises 12, find the domain and codomain of...Ch. 1.8 - In Exercises 12, find the domain and codomain of...Ch. 1.8 - In Exercises 34, find the domain and codomain of...Ch. 1.8 - In Exercises 34, find the domain and codomain of...Ch. 1.8 - In Exercises 56, find the domain and codomain of...Ch. 1.8 - In Exercises 56, find the domain and codomain of...Ch. 1.8 - In Exercises 78, find the domain and codomain of...Ch. 1.8 - In Exercises 78, find the domain and codomain of...Ch. 1.8 - In Exercises 910, find the domain and codomain of...Ch. 1.8 - In Exercises 910, find the domain and codomain of...Ch. 1.8 - In Exercises 1112, find the standard matrix for...Ch. 1.8 - In Exercises 1112, find the standard matrix for...Ch. 1.8 - Find the standard matrix for the transformation T...Ch. 1.8 - Find the standard matrix for the operator T...Ch. 1.8 - Find the standard matrix for the operator T : R 3 ...Ch. 1.8 - Find the standard matrix for the transformation T...Ch. 1.8 - In Exercises 1718, find the standard matrix for...Ch. 1.8 - In Exercises 1718, find the standard matrix for...Ch. 1.8 - In Exercises 1920, find TA(x), and express your...Ch. 1.8 - In Exercises 1920, find TA(x), and express your...Ch. 1.8 - In Exercises 2122, use Theorem 1.8.2 to show that...Ch. 1.8 - In Exercises 2122, use Theorem 1.8.2 to show that...Ch. 1.8 - In Exercises 2324, use Theorem 1.8.2 to show that...Ch. 1.8 - In Exercises 2324, use Theorem 1.8.2 to show that...Ch. 1.8 - A function of the form f(x) = mx + b is commonly...Ch. 1.8 - Show that T(x, y) = (0, 0) defines a matrix...Ch. 1.8 - In Exercises 2728, the images of the standard...Ch. 1.8 - In Exercises 2728, the images of the standard...Ch. 1.8 - Use matrix multiplication to find the reflection...Ch. 1.8 - Use matrix multiplication to find the reflection...Ch. 1.8 - Use matrix multiplication to find the reflection...Ch. 1.8 - Use matrix multiplication to find the reflection...Ch. 1.8 - Use matrix multiplication to find the orthogonal...Ch. 1.8 - Use matrix multiplication to find the orthogonal...Ch. 1.8 - Use matrix multiplication to find the orthogonal...Ch. 1.8 - Use matrix multiplication to find the orthogonal...Ch. 1.8 - Use matrix multiplication to find the image of the...Ch. 1.8 - Use matrix multiplication to find the image of the...Ch. 1.8 - Let T:R2R2 be a linear operator for which the...Ch. 1.8 - Let TA:R2R2 be multiplication by A=[abcd] and let...Ch. 1.8 - Let TA:R3R3 be multiplication by A=[130212453] and...Ch. 1.8 - For each orthogonal projection operator in Table 4...Ch. 1.8 - For each orthogonal projection operator in Table 4...Ch. 1.8 - If multiplication by A rotates a vector x in the...Ch. 1.8 - Find the standard matrix A for the linear...Ch. 1.8 - Find the standard matrix A for the linear...Ch. 1.8 - Let x0 be a nonzero column vector in R2, and...Ch. 1.8 - In a sentence, describe the geometric effect of...Ch. 1.8 - a. Prove: If T:RnRm is a matrix transformation,...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.8 - In parts (a)(g) determine whether the statement is...Ch. 1.9 - In Exercises 14, determine whether the operators...Ch. 1.9 - Prob. 2ECh. 1.9 - In Exercises 14, determine whether the operators...Ch. 1.9 - In Exercises 14, determine whether the operators...Ch. 1.9 - In Exercises 56, let TA and TB be the operators...Ch. 1.9 - In Exercises 56, let TA and TB be the operators...Ch. 1.9 - Find the standard matrix for the stated...Ch. 1.9 - Find the standard matrix for the stated...Ch. 1.9 - Find the standard matrix for the stated...Ch. 1.9 - Find the standard matrix for the stated...Ch. 1.9 - Let T1(x1,x2)=(x1+x2,x1x2) and...Ch. 1.9 - Let T1(x1,x2,x3)=(4x1,2x1+x2,x13x2) and...Ch. 1.9 - Let T1(x1,x2)=(x1x2,2x1x1,3x1) and...Ch. 1.9 - Let T1(x1,x2,x3,x4)=(x1+2x2+3x3,x2x4) and...Ch. 1.9 - Let T1:R2R4 and T2:R4R3 be given by:...Ch. 1.9 - Let T1:R2R3 and T2:R3R4 be given by:...Ch. 1.9 - In Exercises 1718, express the equations in matrix...Ch. 1.9 - In Exercises 1718, express the equations in matrix...Ch. 1.9 - Determine whether the matrix operator T:R2R2...Ch. 1.9 - Determine whether the matrix operator T:R3R3...Ch. 1.9 - In Exercises 2122, determine whether the matrix...Ch. 1.9 - In Exercises 2122, determine whether the matrix...Ch. 1.9 - In Exercises 2324, determine whether TA is...Ch. 1.9 - In Exercises 2324, determine whether TA is...Ch. 1.9 - Let TA:R2R2 be multiplication by A=[0110] a. What...Ch. 1.9 - Let TA=R2R2 be multiplication by...Ch. 1.9 - Prove that the matrix transformations TA and TB...Ch. 1.9 - Let TA and TB be matrix operators on Rn. Prove...Ch. 1.9 - Prove that the matrix operator TA on Rn is...Ch. 1.9 - In parts (a)(g) determine whether the statement is...Ch. 1.9 - In parts (a)(g) determine whether the statement is...Ch. 1.9 - In parts (a)(g) determine whether the statement is...Ch. 1.9 - In parts (a)(g) determine whether the statement is...Ch. 1.9 - In parts (a)(g) determine whether the statement is...Ch. 1.9 - Prob. 6TFCh. 1.9 - In parts (a)(g) determine whether the statement is...Ch. 1.10 - The accompanying figure shows a network in which...Ch. 1.10 - The accompanying figure shows known flow rates of...Ch. 1.10 - The accompanying figure shows a network of one-way...Ch. 1.10 - The accompanying figure shows a network of one-way...Ch. 1.10 - In Exercises 58, analyze the given electrical...Ch. 1.10 - In Exercises 58, analyze the given electrical...Ch. 1.10 - In Exercises 58, analyze the given electrical...Ch. 1.10 - In Exercises 58, analyze the given electrical...Ch. 1.10 - In Exercises 912, write a balanced equation for...Ch. 1.10 - In Exercises 912, write a balanced equation for...Ch. 1.10 - In Exercises 912, write a balanced equation for...Ch. 1.10 - In Exercises 912, write a balanced equation for...Ch. 1.10 - Find the quadratic polynomial whose graph passes...Ch. 1.10 - Find the quadratic polynomial whose graph passes...Ch. 1.10 - Find the cubic polynomial whose graph passes...Ch. 1.10 - The accompanying figure shows the graph of a cubic...Ch. 1.10 - a. Find an equation that represents the family of...Ch. 1.10 - In parts (a)(e) determine whether the statement is...Ch. 1.10 - In parts (a)(e) determine whether the statement is...Ch. 1.10 - In parts (a)(e) determine whether the statement is...Ch. 1.10 - In parts (a)(e) determine whether the statement is...Ch. 1.10 - In parts (a)(e) determine whether the statement is...Ch. 1.10 - Use the method of Example 5 to balance the...Ch. 1.10 - Determine the currents in the accompanying...Ch. 1.11 - An automobile mechanic (M) and a body shop (B) use...Ch. 1.11 - A simple economy produces food (F) and housing...Ch. 1.11 - Consider the open economy described by the...Ch. 1.11 - A company produces Web design, software, and...Ch. 1.11 - In Exercises 56, use matrix inversion to find the...Ch. 1.11 - In Exercises 56, use matrix inversion to find the...Ch. 1.11 - Consider an open economy with consumption matrix...Ch. 1.11 - Consider an open economy with consumption matrix...Ch. 1.11 - Consider an open economy with consumption matrix...Ch. 1.11 - a. Consider an open economy with a consumption...Ch. 1.11 - Prove: If C is an n n matrix whose entries are...Ch. 1.11 - In parts (a)(e) determine whether the statement is...Ch. 1.11 - In parts (a)(e) determine whether the statement is...Ch. 1.11 - In parts (a)(e) determine whether the statement is...Ch. 1.11 - In parts (a)(e) determine whether the statement is...Ch. 1.11 - In parts (a)(e) determine whether the statement is...Ch. 1.11 - The following table describes an open economy with...Ch. 1 - In Exercises 14 the given matrix represents an...Ch. 1 - In Exercises 14 the given matrix represents an...Ch. 1 - In Exercises 14 the given matrix represents an...Ch. 1 - In Exercises 14 the given matrix represents an...Ch. 1 - Use GaussJordan elimination to solve for x and y...Ch. 1 - Use GaussJordan elimination to solve for x and y...Ch. 1 - Find positive integers that satisfy...Ch. 1 - A box containing pennies, nickels, and dimes has...Ch. 1 - Let [a0b2aa440a2b] be the augmented matrix for a...Ch. 1 - For which value(s) of a does the following system...Ch. 1 - Find a matrix K such that AKB = C given that...Ch. 1 - How should the coefficients a, b, and c be chosen...Ch. 1 - In each part, solve the matrix equation for X. a....Ch. 1 - Let A be a square matrix. a. Show that...Ch. 1 - Find values of a, b, and c such that the graph of...Ch. 1 - (Calculus required) Find values of a, b, and c...Ch. 1 - Let Jn be the n n matrix each of whose entries is...Ch. 1 - Show that if a square matrix A satisfies...Ch. 1 - Prove: If B is invertible, then AB1 = B1A if and...Ch. 1 - Prove: If A is invertible, then A + B and I + BA 1...Ch. 1 - Prove: If A is an m n matrix and B is the n 1...Ch. 1 - (Calculus required) If the entries of the...Ch. 1 - (Calculus required) Use part (c) of Exercise 22 to...Ch. 1 - Assuming that the stated inverses exist, prove the...Ch. 1 - Partitioned matrices can be multiplied by the...Ch. 1 - Suppose that an invertible matrix A is partitioned...Ch. 1 - In the special case where matrix A21 in Exercise...Ch. 1 - A linear system whose coefficient matrix has a...Ch. 1 - What can you say about the consistency or...
Additional Math Textbook Solutions
Find more solutions based on key concepts
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
Evaluate the integrals in Exercises 1–34.
9.
University Calculus: Early Transcendentals (4th Edition)
Walking and rowing A boat on the ocean is 4 mi from the nearest point on a straight shoreline; that point is 6 ...
Calculus: Early Transcendentals (2nd Edition)
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
For each of the following, determine the constant c so that f(x) satisfies the conditions of being a pmf for a ...
Probability And Statistical Inference (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Question 4 Find the value of the first element for the first row of the inverse matrix of matrix B. 3 Not yet answered B = Marked out of 5.00 · (³ ;) Flag question 7 [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places] Answer:arrow_forwardQuestion 2 Not yet answered Multiply the following Matrices together: [77-4 A = 36 Marked out of -5 -5 5.00 B = 3 5 Flag question -6 -7 ABarrow_forwardAssume {u1, U2, u3, u4} does not span R³. Select the best statement. A. {u1, U2, u3} spans R³ if u̸4 is a linear combination of other vectors in the set. B. We do not have sufficient information to determine whether {u₁, u2, u3} spans R³. C. {U1, U2, u3} spans R³ if u̸4 is a scalar multiple of another vector in the set. D. {u1, U2, u3} cannot span R³. E. {U1, U2, u3} spans R³ if u̸4 is the zero vector. F. none of the abovearrow_forward
- Select the best statement. A. If a set of vectors includes the zero vector 0, then the set of vectors can span R^ as long as the other vectors are distinct. n B. If a set of vectors includes the zero vector 0, then the set of vectors spans R precisely when the set with 0 excluded spans Rª. ○ C. If a set of vectors includes the zero vector 0, then the set of vectors can span Rn as long as it contains n vectors. ○ D. If a set of vectors includes the zero vector 0, then there is no reasonable way to determine if the set of vectors spans Rn. E. If a set of vectors includes the zero vector 0, then the set of vectors cannot span Rn. F. none of the abovearrow_forwardWhich of the following sets of vectors are linearly independent? (Check the boxes for linearly independent sets.) ☐ A. { 7 4 3 13 -9 8 -17 7 ☐ B. 0 -8 3 ☐ C. 0 ☐ D. -5 ☐ E. 3 ☐ F. 4 THarrow_forward3 and = 5 3 ---8--8--8 Let = 3 U2 = 1 Select all of the vectors that are in the span of {u₁, u2, u3}. (Check every statement that is correct.) 3 ☐ A. The vector 3 is in the span. -1 3 ☐ B. The vector -5 75°1 is in the span. ГОЛ ☐ C. The vector 0 is in the span. 3 -4 is in the span. OD. The vector 0 3 ☐ E. All vectors in R³ are in the span. 3 F. The vector 9 -4 5 3 is in the span. 0 ☐ G. We cannot tell which vectors are i the span.arrow_forward
- (20 p) 1. Find a particular solution satisfying the given initial conditions for the third-order homogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y(3)+2y"-y-2y = 0; y(0) = 1, y'(0) = 2, y"(0) = 0; y₁ = e*, y2 = e¯x, y3 = e−2x (20 p) 2. Find a particular solution satisfying the given initial conditions for the second-order nonhomogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y"-2y-3y = 6; y(0) = 3, y'(0) = 11 yc = c₁ex + c2e³x; yp = −2 (60 p) 3. Find the general, and if possible, particular solutions of the linear systems of differential equations given below using the eigenvalue-eigenvector method. (See Section 7.3 in your textbook if you need a review of the subject.) = a) x 4x1 + x2, x2 = 6x1-x2 b) x=6x17x2, x2 = x1-2x2 c) x = 9x1+5x2, x2 = −6x1-2x2; x1(0) = 1, x2(0)=0arrow_forwardFind the perimeter and areaarrow_forwardAssume {u1, U2, us} spans R³. Select the best statement. A. {U1, U2, us, u4} spans R³ unless u is the zero vector. B. {U1, U2, us, u4} always spans R³. C. {U1, U2, us, u4} spans R³ unless u is a scalar multiple of another vector in the set. D. We do not have sufficient information to determine if {u₁, u2, 43, 114} spans R³. OE. {U1, U2, 3, 4} never spans R³. F. none of the abovearrow_forward
- Assume {u1, U2, 13, 14} spans R³. Select the best statement. A. {U1, U2, u3} never spans R³ since it is a proper subset of a spanning set. B. {U1, U2, u3} spans R³ unless one of the vectors is the zero vector. C. {u1, U2, us} spans R³ unless one of the vectors is a scalar multiple of another vector in the set. D. {U1, U2, us} always spans R³. E. {U1, U2, u3} may, but does not have to, span R³. F. none of the abovearrow_forwardLet H = span {u, v}. For each of the following sets of vectors determine whether H is a line or a plane. Select an Answer u = 3 1. -10 8-8 -2 ,v= 5 Select an Answer -2 u = 3 4 2. + 9 ,v= 6arrow_forwardSolve for the matrix X: X (2 7³) x + ( 2 ) - (112) 6 14 8arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY