Chapter 1.10, Problem 1G

The spreadsheet summarizes the results for one student on a 15-question math test with partial credit awarded.

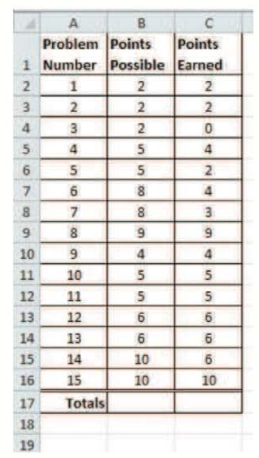
Complete the totals at the bottom of each column using addition.

To determine

To calculate: The total of possible points and points earned in the following table:

Problem number	Points possible	Points earned
1	2	2
2	2	2
3	2	0
4	5	4
5	5	2
6	8	4
7	8	3
8	9	9
9	4	4
10	5	5
11	5	5
12	6	6
13	6	6
14	10	6
15	10	10
Totals

Answer to Problem 1G

Solution:

The total of possible points is $87$ and total of earned points is $68$.

Explanation of Solution

Given Information:

The provided table shows points earned by a student in $15$ questions.

Problem number	Points possible	Points earned
1	2	2
2	2	2
3	2	0
4	5	4
5	5	2
6	8	4
7	8	3
8	9	9
9	4	4
10	5	5
11	5	5
12	6	6
13	6	6
14	10	6
15	10	10
Totals

Calculation:

The total of possible points is sum of all the numbers in the column of possible points.

That is,

$\begin{array}{c}\text{Total possible points}=2+2+2+5+5+8+8+9+4+5+5+6+6+10+10\\ =87\end{array}$

Now, the total earned points is sum of all the numbers in the column of earned points.

That is,

$\begin{array}{c}\text{Total earned points}=2+2+0+4+2+4+3+9+4+5+5+6+6+6+10\\ =68\end{array}$

Therefore, total possible is points is $87$ and total earned points is $68$.