
Calculus of a Single Variable
11th Edition
ISBN: 9781337275361
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 1.1, Problem 6E
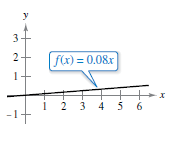
Precalculus or Calculus In Exercises 3-6.decide whether the problem can be solved using precalculus or whether calculus is required. If the problem can be solved using precalculus, solve it. If the problem seems to require calculus, explain your reasoning and use a graphical or numerical approach to estimate the solution.
A bicyclist is riding on a path modeled by the function
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem 11 (a) A tank is discharging water through an orifice at a depth of T
meter below the surface of the water whose area is A m². The
following are the values of a for the corresponding values of A:
A 1.257 1.390
x 1.50 1.65
1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650
1.80 1.95 2.10 2.25 2.40 2.55 2.70
2.85
Using the formula
-3.0
(0.018)T =
dx.
calculate T, the time in seconds for the level of the water to drop
from 3.0 m to 1.5 m above the orifice.
(b) The velocity of a train which starts from rest is given by the fol-
lowing table, the time being reckoned in minutes from the start
and the speed in km/hour:
| † (minutes) |2|4 6 8 10 12
14 16 18 20
v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0
Estimate approximately the total distance ran in 20 minutes.
X
Solve numerically:
= 0,95
In x
X
Solve numerically:
= 0,95
In x
Chapter 1 Solutions
Calculus of a Single Variable
Ch. 1.1 - CONCEPT CHECK Precalculus and Calculus Describe...Ch. 1.1 - CONCEPT CHECK Secant and Tangent Lines Discuss the...Ch. 1.1 - Precalculus or Calculus In Exercises 3-6.decide...Ch. 1.1 - Precalculus or Calculus In Exercises 3-6.decide...Ch. 1.1 - Precalculus or Calculus In Exercises 3-6.decide...Ch. 1.1 - Precalculus or Calculus In Exercises 3-6.decide...Ch. 1.1 - Secant Lines Consider the function f(x)=x and the...Ch. 1.1 - Secant Lines Consider the function f(x) = 6x x2...Ch. 1.1 - Approximating Area Use the rectangles in each...Ch. 1.1 - HOW DO YOU SEE IT? How would you describe the...
Ch. 1.1 - Length of a Curve Consider the length of the graph...Ch. 1.2 - Describing Notation Write a brief description of...Ch. 1.2 - CONCEPT CHECK Limits That Fail to Exist Identify...Ch. 1.2 - Formal Definition of Limit Given the limit...Ch. 1.2 - CONCEPT CHECK Functions and Limits Is the limit of...Ch. 1.2 - Estimating a Limit Numerically In Exercises 5-10,...Ch. 1.2 - Estimating a Limit Numerically In Exercises 5-10,...Ch. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Estimating a Limit Numerically In Exercises 11-18,...Ch. 1.2 - Estimating a Limit Numerically In Exercises 11-18,...Ch. 1.2 - Estimating a Limit Numerically In Exercises 11-18,...Ch. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Estimating a Limit Numerically In Exercises 11-18,...Ch. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Limits That Fail to Exist In Exercises 19 and 20,...Ch. 1.2 - Limits That Fail to Exist In Exercises 19 and 20,...Ch. 1.2 - Prob. 21ECh. 1.2 - Finding a Limit Graphically In Exercises 21-28,...Ch. 1.2 - Finding a Limit Graphically In Exercises 21-28,...Ch. 1.2 - Finding a Limit Graphically In Exercises 21-28,...Ch. 1.2 - Finding a Limit Graphically In Exercises 21-28,...Ch. 1.2 - Finding a Limit Graphically In Exercises 21-28,...Ch. 1.2 - Prob. 27ECh. 1.2 - Finding a Limit Graphically In Exercises 21-28,...Ch. 1.2 - Prob. 29ECh. 1.2 - Graphical Reasoning In Exercises 29 and 30, use...Ch. 1.2 - Limits of a Piecewise Function In Exercises 31 and...Ch. 1.2 - Limits of a Piecewise Function In Exercises 31 and...Ch. 1.2 - Sketching a Graph In Exercises 33 and 34, sketch a...Ch. 1.2 - Sketching a Graph In Exercises 33 and 34, sketch a...Ch. 1.2 - Finding a for a Given The graph of f(x)=x+1 is...Ch. 1.2 - Prob. 36ECh. 1.2 - Finding a for a Given The graph of f(x)=21x is...Ch. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Finding a for a Given In Exercises 39-44. find...Ch. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Using the Definition of Limit In Exercises 45-56,...Ch. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Finding a Limit What is the limit of g(x)=x as x...Ch. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Estimating a Limit Consider the function...Ch. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - HOW DO YOU SEE IT? Use the graph of f to identify...Ch. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Proof (a) Given that limx0(3x+1)(3x1)x2+0.01=0.01...Ch. 1.2 - Prob. 85ECh. 1.2 - A right circular cone has base of radius 1 and...Ch. 1.2 - Prob. 6ECh. 1.2 - Estimating a Limit Numerically In Exercises 5-10,...Ch. 1.3 - CONCEPT CHECK Polynomial Function Describe how to...Ch. 1.3 - Indeterminate Form What is meant by an...Ch. 1.3 - Squeeze Theorem In your own words, explain the...Ch. 1.3 - CONCEPT CHECK Special Limits List the two special...Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22. find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Finding a Limit In Exercises 5-22, find the limit....Ch. 1.3 - Prob. 23ECh. 1.3 - Finding Limits In Exercises 23-26, Find the...Ch. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Prob. 28ECh. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Prob. 31ECh. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Prob. 36ECh. 1.3 - Evaluating Limits In Exercises 37-40, use the...Ch. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Finding a Limit In Exercises 41-46, write a...Ch. 1.3 - Finding a Limit In Exercises 41-46, write a...Ch. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Finding a Limit In Exercises 41-46, write a...Ch. 1.3 - Finding a Limit In Exercises 41-46, write a...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 4762, find the limit....Ch. 1.3 - Finding a Limit In Exercises 4762, find the limit....Ch. 1.3 - Prob. 50ECh. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit In Exercises 47-62, find the...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Prob. 70ECh. 1.3 - Prob. 71ECh. 1.3 - Finding a Limit of a Trigonometric Function In...Ch. 1.3 - Prob. 73ECh. 1.3 - Prob. 74ECh. 1.3 - Graphical, Numerical, and Analytic Analysis In...Ch. 1.3 - Graphical, Numerical, and Analytic Analysis In...Ch. 1.3 - Graphical, Numerical, and Analytic Analysis In...Ch. 1.3 - Prob. 78ECh. 1.3 - Prob. 79ECh. 1.3 - Prob. 80ECh. 1.3 - Prob. 81ECh. 1.3 - Prob. 82ECh. 1.3 - Prob. 83ECh. 1.3 - Prob. 84ECh. 1.3 - Finding a Limit In Exercises 83-90, find...Ch. 1.3 - Finding a Limit In Exercises 83-90, find...Ch. 1.3 - Finding a Limit In Exercises 83-90, find...Ch. 1.3 - Finding a Limit In Exercises 83-90, find...Ch. 1.3 - Prob. 89ECh. 1.3 - Prob. 90ECh. 1.3 - Using the Squeeze Theorem In Exercises 91 and 92,...Ch. 1.3 - Prob. 92ECh. 1.3 - Prob. 93ECh. 1.3 - Prob. 94ECh. 1.3 - Using the Squeeze Theorem In Exercises 93-96, use...Ch. 1.3 - Prob. 96ECh. 1.3 - Prob. 97ECh. 1.3 - Writing Functions Write a function of each...Ch. 1.3 - Prob. 99ECh. 1.3 - Prob. 100ECh. 1.3 - Free-Falling Object In Exercises 101 and 102. use...Ch. 1.3 - Free-Falling Object In Exercises 101 and 102. use...Ch. 1.3 - Free-Falling Object In Exercises 103 and 104, use...Ch. 1.3 - Free-Falling Object In Exercises 103 and 104, use...Ch. 1.3 - Finding Functions Find two functions f and g such...Ch. 1.3 - Prob. 106ECh. 1.3 - Prob. 107ECh. 1.3 - Proof Prove Property 3 of Theorem 1.1. (You may...Ch. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Prob. 111ECh. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Think About ItWhen using a graphing utility to...Ch. 1.3 - Prob. 115ECh. 1.3 - Prob. 116ECh. 1.3 - Prob. 117ECh. 1.3 - Prob. 118ECh. 1.3 - Prob. 119ECh. 1.3 - True or False? In Exercises 115120, determine...Ch. 1.3 - Prob. 121ECh. 1.3 - Prob. 122ECh. 1.3 - Graphical Reasoning Consider f(x)=secx1x2. (a)...Ch. 1.3 - Approximation (a) Find limx01cosxx2. (b) Use your...Ch. 1.4 - CONCEPT CHECK Continuity In your own words,...Ch. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Limits and Continuity In Exercises 5-10, use the...Ch. 1.4 - Limits and Continuity In Exercises 5-10, use the...Ch. 1.4 - Limits and Continuity In Exercises 5-10, use the...Ch. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Limits and Continuity In Exercises 5-10, use the...Ch. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Prob. 20ECh. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Finding a Limit In Exercises 11-30, find the limit...Ch. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Continuity on a Closed Interval In Exercises...Ch. 1.4 - Prob. 39ECh. 1.4 - Removable and Nonremovable Discontinuities In...Ch. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Removable and Nonremovable Discontinuities In...Ch. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Continuity of a Composite Function In Exercises...Ch. 1.4 - Continuity of a Composite Function In Exercises...Ch. 1.4 - Prob. 71ECh. 1.4 - Finding Discontinuities Using Technology In...Ch. 1.4 - Prob. 73ECh. 1.4 - Prob. 74ECh. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.4 - Prob. 77ECh. 1.4 - Prob. 78ECh. 1.4 - Prob. 79ECh. 1.4 - Prob. 80ECh. 1.4 - Prob. 81ECh. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.4 - Prob. 85ECh. 1.4 - Existence of a Zero In Exercises 83-86, explain...Ch. 1.4 - Prob. 87ECh. 1.4 - Prob. 88ECh. 1.4 - Prob. 89ECh. 1.4 - Prob. 90ECh. 1.4 - Prob. 91ECh. 1.4 - Prob. 92ECh. 1.4 - Prob. 93ECh. 1.4 - Prob. 94ECh. 1.4 - Prob. 95ECh. 1.4 - Prob. 96ECh. 1.4 - Prob. 97ECh. 1.4 - Prob. 98ECh. 1.4 - Prob. 99ECh. 1.4 - Using the Intermediate Value Theorem In Exercises...Ch. 1.4 - Prob. 101ECh. 1.4 - Prob. 102ECh. 1.4 - Prob. 103ECh. 1.4 - EXPLORING CONCEPTS Removable and Nonremovable...Ch. 1.4 - Prob. 105ECh. 1.4 - Prob. 106ECh. 1.4 - Prob. 107ECh. 1.4 - Prob. 108ECh. 1.4 - Prob. 109ECh. 1.4 - Prob. 110ECh. 1.4 - Prob. 111ECh. 1.4 - Prob. 112ECh. 1.4 - Prob. 113ECh. 1.4 - Prob. 114ECh. 1.4 - Prob. 115ECh. 1.4 - Prob. 116ECh. 1.4 - Prob. 117ECh. 1.4 - Prob. 118ECh. 1.4 - Prob. 119ECh. 1.4 - Signum Function The signum function is defined by...Ch. 1.4 - Prob. 121ECh. 1.4 - Creating Models A swimmer crosses a pool of width...Ch. 1.4 - Prob. 123ECh. 1.4 - Prob. 124ECh. 1.4 - Prob. 125ECh. 1.4 - Prob. 126ECh. 1.4 - Prob. 127ECh. 1.4 - Prob. 128ECh. 1.4 - Prob. 129ECh. 1.4 - Prob. 130ECh. 1.5 - Infinite Limit In your own words, describe the...Ch. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Determining Infinite Limits from a Graph In...Ch. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Determining Infinite Limits from a Graph In...Ch. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Numerical and Graphical Analysis In Exercises...Ch. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Numerical and Graphical Analysis In Exercises...Ch. 1.5 - Finding Vertical Asymptotes In Exercises 17-32....Ch. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Finding Vertical Asymptotes In Exercises 17-32....Ch. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Finding Vertical Asymptotes In Exercises 17-32....Ch. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Finding a One-Sided Limit In Exercises 37-50, find...Ch. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - HOW DO YOU SEE IT? For a quantity of gas at a...Ch. 1.5 - Rate of Change A 25-foot ladder is leaning against...Ch. 1.5 - Average Speed On a trip of d miles to another...Ch. 1.5 - Numerical and Graphical Analysis Consider the...Ch. 1.5 - Numerical and Graphical Reasoning A crossed belt...Ch. 1.5 - Prob. 65ECh. 1.5 - Prob. 66ECh. 1.5 - Prob. 67ECh. 1.5 - Prob. 68ECh. 1.5 - Prob. 69ECh. 1.5 - Prob. 70ECh. 1.5 - Prob. 71ECh. 1.5 - Prob. 72ECh. 1.5 - Prob. 73ECh. 1.5 - Prob. 74ECh. 1.5 - Prob. 75ECh. 1.5 - Prob. 76ECh. 1 - Precalculus or Calculus In Exercises 1 and 2,...Ch. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 15RECh. 1 - Prob. 14RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Finding a Limit In Exercises 1128, find the limit....Ch. 1 - Prob. 26RECh. 1 - Finding a Limit In Exercises 1128, find the limit....Ch. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Free-Falling Object In Exercises 37 and 38. use...Ch. 1 - Free-Falling Object In Exercises 37 and 38. use...Ch. 1 - Prob. 39RECh. 1 - Finding a Limit In Exercises 39-50, find the limit...Ch. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - Prob. 84RECh. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - Environment A utility company burns coal to...Ch. 1 - Perimeter Let P (x. y) be a point on the parabola...Ch. 1 - Prob. 2PSCh. 1 - Prob. 3PSCh. 1 - Tangent Line Let P (3, 4) be a point on the circle...Ch. 1 - Prob. 5PSCh. 1 - Prob. 6PSCh. 1 - Prob. 7PSCh. 1 - Prob. 8PSCh. 1 - Prob. 9PSCh. 1 - Prob. 10PSCh. 1 - Prob. 11PSCh. 1 - Escape Velocity To escape Earth's gravitational...Ch. 1 - Pulse Function For positive numbers ab, the pulse...Ch. 1 - Proof Let a be a nonzero constant. Prove that if...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Please as many detarrow_forward8–23. Sketching vector fields Sketch the following vector fieldsarrow_forward25-30. Normal and tangential components For the vector field F and curve C, complete the following: a. Determine the points (if any) along the curve C at which the vector field F is tangent to C. b. Determine the points (if any) along the curve C at which the vector field F is normal to C. c. Sketch C and a few representative vectors of F on C. 25. F = (2½³, 0); c = {(x, y); y − x² = 1} 26. F = x (23 - 212) ; C = {(x, y); y = x² = 1}) , 2 27. F(x, y); C = {(x, y): x² + y² = 4} 28. F = (y, x); C = {(x, y): x² + y² = 1} 29. F = (x, y); C = 30. F = (y, x); C = {(x, y): x = 1} {(x, y): x² + y² = 1}arrow_forward
- ٣/١ B msl kd 180 Ka, Sin (1) I sin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 G 5005 1000 s = 1000-950 Copper bosses 5kW Rotor input 5 0.05 : loo kw 6) 1 /0001 ined sove in peaper I need a detailed solution on paper please وه اذا ميريد شرح الكتب فقط ١٥٠ DC 7) rotor a ' (y+xlny + xe*)dx + (xsiny + xlnx + dy = 0. Q1// Find the solution of: ( 357arrow_forward۳/۱ R₂ = X2 2) slots per pole per phase 3/31 B. 180 msl Kas Sin (I) 1sin() sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30): 0.866 4) Rotating 5) Synchronous speeds 120×50 looo G 1000-950 1000 Copper losses 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 Find the general solution of the following equations: QI//y(4)-16y= 0. Find the general solution of the following equations: Q2ll yll-4y/ +13y=esinx.arrow_forwardR₂ = X2 2) slots per pole per phase = 3/31 B-180 60 msl kd Kas Sin () 2 I sin (6) sin(30) Sin (30) اذا مريد شرح الكتب بس 0 بالفراغ 3 Cos (30) 0.866 4) Rotating ined sove in peaper 5) Synchronous speed s 120×50 6 s = 1000-950 1000 Copper losses 5kw Rotor input 5 0.05 6) 1 loo kw اذا ميريد شرح الكتب فقط Look 7) rotov DC I need a detailed solution on paper please 0 64 Solve the following equations: 0 Q1// Find the solution of: ( y • with y(0) = 1. dx x²+y²arrow_forward
- R₂ = X2 2) slots per pole per phase = 3/3 1 B-180-60 msl Ka Sin (1) Isin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 s = 1000-950 1000 Copper losses 5kw Rotor input 5 6) 1 0.05 G 50105 loo kw اذا ميريد شرح الكتب فقط look 7) rotov DC ined sove in peaper I need a detailed solution on paper please 064 2- A hot ball (D=15 cm ) is cooled by forced air T.-30°C, the rate of heat transfer from the ball is 460.86 W. Take for the air -0.025 Wim °C and Nu=144.89, find the ball surface temperature a) 300 °C 16 b) 327 °C c) 376 °C d) None か = 750 01arrow_forwardDon't do 14. Please solve 19arrow_forwardPlease solve 14 and 15arrow_forward
- 1. Consider the following system of equations: x13x2 + 4x3 - 5x4 = 7 -2x13x2 + x3 - 6x4 = 7 x16x213x3 - 21x4 = 28 a) Solve the system. Write your solution in parametric and vector form. b) What is a geometric description of the solution. 7 c) Is v = 7 in the span of the set S= [28. 1 HE 3 -5 3 ·6 ? If it is, write v 6 as a linear combination of the vectors in S. Justify. d) How many solutions are there to the associated homogeneous system for the system above? Justify. e) Let A be the coefficient matrix from the system above. Find the set of all solutions to Ax = 0. f) Is there a solution to Ax=b for all b in R³? Justify.arrow_forward4. Suppose that A is made up of 5 column vectors in R³, and suppose that the rank(A)=3. a. How many solutions are there to Ax=0? Justify. b. What is a geometric description for the nullspace(A)? Justify. c. Do the column vectors of A span R³? Justify. d. Is A invertible? Justify.arrow_forward3. Suppose that A is 5 x 5 and rank(A)=4. Use this information to answer the following. a. Give a geometric description of nullspace(A). Justify. b. Is A invertible? Justify. c. Give a geometric description of the span of the column vectors of A. What space are the column vectors of A in? Justify. d. What is determinant of A? Justify.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY