Chapter 1.1, Problem 69E

A bakery owner knows that customers buy a total of q cakes when the price, p, is no more than p = d(q) = 20 − q∕20 dollars. She is willing to make and supply as many as q cakes at a price of p = s(q) = 11 + q∕40 dollars each. (The graphs of the functions d(q) and s(q) are called a demand curve and a supply curve, respectively.) The graphs of d(q) and s(q) are in Figure 1.22.

1. (a) Why, in terms of the context, is the slope of d(q) negative and the slope of s(q) positive?
2. (b) Is each of the ordered pairs (q, p) a solution to the inequality p ≤ 20 − q∕20? Interpret your answers in terms of the context.

   (60, 18) (120, 12)

3. (c) Graph in the qp-plane the solution set of the system of inequalities p ≤ 20 − q∕20, p ≥ 11 + q∕40. What does this solution set represent in terms of the context?
4. (d) What is the rightmost point of the solution set you graphed in part (c)? Interpret your answer in terms of the context.

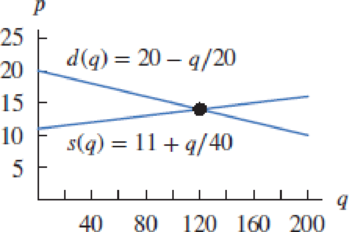
Figure 1.22