
a.
To draw the next two figures of the pattern given in the problem.
The next two figures of the pattern: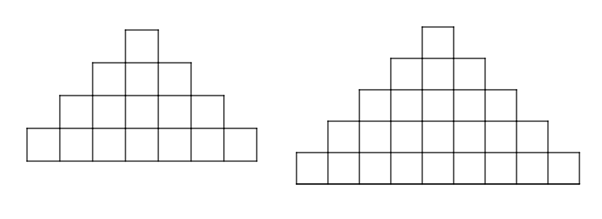
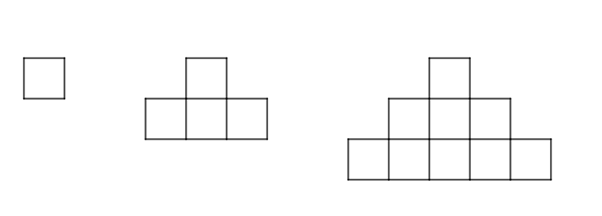
Given the pattern:
Calculation:
Observe the pattern:
The pattern is constructed of identical squares arranged symmetrically. Each figure of the pattern is constructed from the previous one by adding an extended copy of the last row to the bottom of it extended by two squares on either ends of it.
Thus, the fourth figure will have all the squares of the third one and one more row added to the bottom of it containing
squares as drawn below:
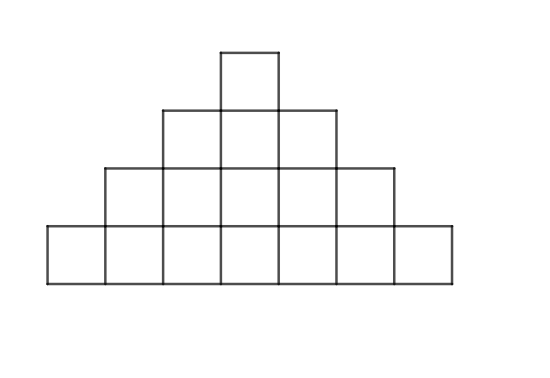
Likewise, the fifth figure of the pattern will have all the squares of the fourth one and one more row added to the bottom of it containing
squares as:
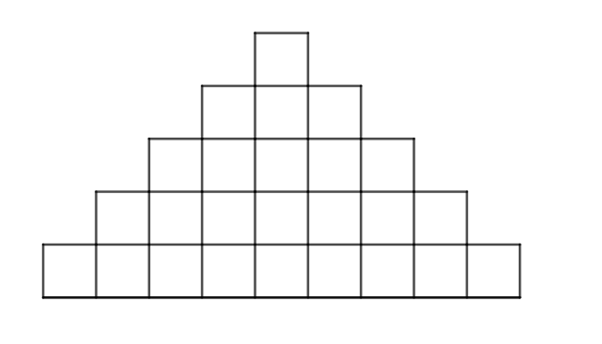
Thus, the fourth and fifth figures of the pattern:
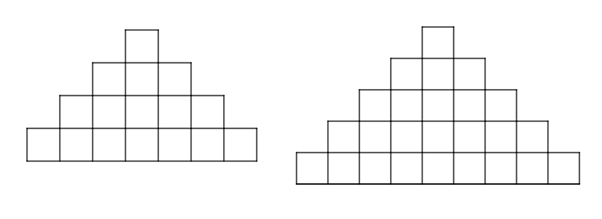
Conclusion:
The next two figures of the pattern:
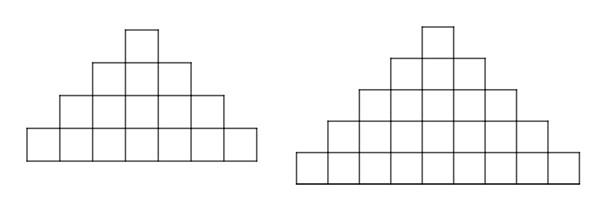
b.
To copy and complete the table given in the problem.
The completed table:
| Figure (Input) | Process Column | Number of squares (Output) |
Given the incomplete table:
| Figure (Input) | Process Column | Number of squares (Output) |
Calculation:
Observe that the first figure of the pattern comes in the first column and it has only one square.
Thus, the process column of the input
Now, note that that the second figure of the pattern comes in the second column and it has only four squares.
Thus, the process column of the input
Proceed in a similar way and find all the process column values and output values corresponding to each other inputs:
Incorporate all the findings into the table and complete it:
| Figure (Input) | Process Column | Number of squares (Output) |
Conclusion:
The completed table:
| Figure (Input) | Process Column | Number of squares (Output) |
c.
To determine the number of squares in the
It is observed from the table of inputs and outputs of the pattern that the output is
Then, it is concluded that the
Calculation:
Observe the table found in the previous part:
The output of
The output of
Analysing the table in a similar way, it may be observed that, the output of
Conclusion:
It is observed from the table of inputs and outputs of the pattern that the output of the pattern is
Then, it is concluded that the
Chapter 1 Solutions
High School Math 2015 Common Core Algebra 2 Student Edition Grades 10/11
- Solve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work. Dear Student If You Face any issue let me know i will solve your all doubt. I will provide solution again in more detail systematic and organized way. I would also like my last 3 questions credited to mearrow_forward
- Dalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work.arrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1arrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5arrow_forward
- Write an equation for the function shown. You may assume all intercepts and asymptotes are on integers. The blue dashed lines are the asymptotes. 10 9- 8- 7 6 5 4- 3- 2 4 5 15-14-13-12-11-10 -9 -8 -7 -6 -5 -4 -3 -2 1 1 2 3 -1 -2 -3 -4 1 -5 -6- -7 -8- -9 -10+ 60 7 8 9 10 11 12 13 14 15arrow_forwardUse the graph of the polynomial function of degree 5 to identify zeros and multiplicity. Order your zeros from least to greatest. -6 3 6+ 5 4 3 2 1 2 -1 -2 -3 -4 -5 3 4 6 Zero at with multiplicity Zero at with multiplicity Zero at with multiplicityarrow_forwardUse the graph to identify zeros and multiplicity. Order your zeros from least to greatest. 6 5 4 -6-5-4-3-2 3 21 2 1 2 4 5 ૪ 345 Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity པ་arrow_forward
- Use the graph to write the formula for a polynomial function of least degree. -5 + 4 3 ♡ 2 12 1 f(x) -1 -1 f(x) 2 3. + -3 12 -5+ + xarrow_forwardUse the graph to identify zeros and multiplicity. Order your zeros from least to greatest. 6 -6-5-4-3-2-1 -1 -2 3 -4 4 5 6 a Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity Zero at with multiplicityarrow_forwardUse the graph to write the formula for a polynomial function of least degree. 5 4 3 -5 -x 1 f(x) -5 -4 -1 1 2 3 4 -1 -2 -3 -4 -5 f(x) =arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





