Chapter 11, Problem 30QP

Systematic versus Unsystematic Risk. Consider the following information on Stocks I and II:

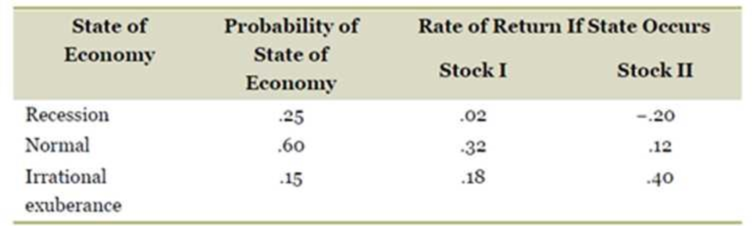
 The market risk premium is 7 percent, and the risk-free rate is 4 percent. Which stock has the most systematic risk? Which one has the most unsystematic risk? Which stock is “riskier”? Explain

Summary Introduction

To determine: The stock that has the most systematic risk and the most unsystematic risk.

Introduction:

Systematic risk refers to the market-specific risk that affects all the stocks in the market.

Unsystematic risk refers to the company-specific risk that affects only the individual company.

Explanation of Solution

Given information:

The probability of having a recession, normal economy, and irrational exuberance is 0.25, 0.60, and 0.15 respectively. Stock I will yield 2%, 32%, and 18% when there is a recession, normal economy, and irrational exuberance respectively.

Stock II will yield −20%, 12%, and 40% when there is a recession, normal economy, and irrational exuberance respectively. The market risk premium is 7% and the risk-free rate is 4%.

The formula to calculate the expected return on the stock:

$\text{Expected returns}=\left[\begin{array}{l}\left(\text{Possible returns}\left(R_1\right)\times \text{Probability}\left(P_1\right)\right)\\ +\mathrm{...}+\left(\text{Possible returns}\left(R_n\right)\times \text{Probability}\left(P_n\right)\right)\end{array}\right]$

The formula to calculate the beta of the stock:

$E(R_i)=R_f+\left[E(R_M)-R_f\right]\times {\beta }_i$

Where,

E(R_i) refers to the expected return on a risky asset

R_f  refers to the risk-free rate

E(R_M) refers to the expected return on the market portfolio

β_i refers to the beta coefficient of the risky asset relative to the market portfolio

The formula to calculate the standard deviation:

$\begin{array}{l}\text{Standard}\\ \text{deviation}\end{array}\}=\sqrt{\left(\begin{array}{l}\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_1\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{ Probability}\left(P_1\right)\end{array}\right]\\ +\mathrm{...}+\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_n\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{ Probability}\left(P_n\right)\end{array}\right]\end{array}\right)}$

Compute the expected return on Stock I:

R₁ is the returns during the recession. The probability of having a recession is P₁. Similarly, R₂ is the returns in a normal economy. The probability of having a normal is P₂. R₃ is the returns in irrational exuberance. The probability of having an irrational exuberance is P₃.

$\begin{array}{c}\text{Expected returns}=\left[\begin{array}{l}\left(\text{Possible returns}\left(R_1\right)\times \text{Probability}\left(P_1\right)\right)\\ +\left(\text{Possible returns}\left(R_2\right)\times \text{Probability}\left(P_2\right)\right)\\ +\left(\text{Possible returns}\left(R_2\right)\times \text{Probability}\left(P_2\right)\right)\end{array}\right]\\ =\left(\left(0.25\right)\times 0.02\right)+\left(0.60\times 0.32\right)+\left(0.15\times 0.18\right)\\ =\left(0.005+0.192+0.027\right)\\ =0.2240\end{array}$

Hence, the expected return on Stock I is 0.2240 or 22.40 percent.

Compute the beta of Stock I:

$\begin{array}{c}E(R_I)=R_f+\left[E(R_M)-R_f\right]\times {\beta }_I\\ 0.2240=0.04+\left[0.07\right]\times {\beta }_I\\ \left(0.2240-0.04\right)=\text{0}\text{.07}{\beta }_I\\ \frac{0.184}{0.07}={\beta }_I\\ 2.63={\beta }_I\end{array}$

Hence, the beta of Stock I is 2.63.

Compute the standard deviation of Stock I:

R₁ is the returns during the recession. The probability of having a recession is P₁. Similarly, R₂ is the returns in a normal economy. The probability of having a normal is P₂. R₃ is the returns in irrational exuberance. The probability of having an irrational exuberance is P₃.

$\begin{array}{c}\begin{array}{l}\text{Standard}\\ \text{deviation}\end{array}\}=\sqrt{\left(\begin{array}{l}\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_1\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{}\text{ Probability}\left(P_1\right)\end{array}\right]\\ +\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_2\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{Probability}\left(P_2\right)\end{array}\right]\\ +\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_3\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{Probability}\left(P_3\right)\end{array}\right]\end{array}\right)}\\ =\sqrt{\left[\begin{array}{l}\left[{\left(0.02-0.2240\right)}^2\times 0.25\right]+\left[{\left(0.32-0.2240\right)}^2\times 0.60\right]\\ +\left[{\left(0.18-0.2240\right)}^2\times 0.15\right]\end{array}\right]}\\ =\sqrt{\left({\left(-0.204\right)}^2\times 0.25\right)+\left({\left(0.096\right)}^2\times 0.60\right)+\left({\left(-0.044\right)}^2\times 0.15\right)}\\ =\sqrt{\left(0.041616\times 0.25\right)+\left(0.009216\times 0.60\right)+\left(0.001936\times 0.15\right)}\end{array}$

$\begin{array}{c}=\sqrt{0.010404+0.0055296+0.0002904}\\ =\sqrt{0.016224}\\ =0.1274\end{array}$

Hence, the standard deviation of Stock I is 0.1274 or 12.74%.

Compute the expected return on Stock II:

R₁ is the returns during the recession. The probability of having a recession is P₁. Similarly, R₂ is the returns in a normal economy. The probability of having a normal is P₂. R₃ is the returns in irrational exuberance. The probability of having an irrational exuberance is P₃.

$\begin{array}{c}\text{Expected returns}=\left[\begin{array}{l}\left(\text{Possible returns}\left(R_1\right)\times \text{Probability}\left(P_1\right)\right)\\ +\left(\text{Possible returns}\left(R_2\right)\times \text{Probability}\left(P_2\right)\right)\\ +\left(\text{Possible returns}\left(R_2\right)\times \text{Probability}\left(P_2\right)\right)\end{array}\right]\\ =\left(\left(-0.20\right)\times \left(0.25\right)\right)+\left(0.12\times 0.60\right)+\left(0.40\times 0.15\right)\\ =\left(-0.05+0.072+0.06\right)\\ =0.0820\end{array}$

Hence, the expected return on Stock II is 0.0820 or 8.20 percent.

Compute the beta of Stock II:

$\begin{array}{c}E(R_{II})=R_f+\left[E(R_M)-R_f\right]\times {\beta }_{II}\\ 0.0820=0.04+\left[0.07\right]\times {\beta }_{II}\\ \left(0.0820-0.04\right)=0.07{\beta }_{II}\\ \frac{\text{0}\text{.042}}{0.07}={\beta }_{II}\\ 0.6={\beta }_{II}\end{array}$

Hence, the beta of Stock II is 0.6.

Compute the standard deviation of Stock II:

R₁ is the returns during the recession. The probability of having a recession is P₁. Similarly, R₂ is the returns in a normal economy. The probability of having a normal is P₂. R₃ is the returns in irrational exuberance. The probability of having an irrational exuberance is P₃.

$\begin{array}{c}\begin{array}{l}\text{Standard}\\ \text{deviation}\end{array}\}=\sqrt{\left(\begin{array}{l}\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_1\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{}\text{ Probability}\left(P_1\right)\end{array}\right]\\ +\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_2\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{Probability}\left(P_2\right)\end{array}\right]\\ +\left[\begin{array}{l}{\left(\text{Possible returns}\left(R_3\right)-\text{Expected returns}E\left(R\right)\right)}^2\\ \times \text{Probability}\left(P_3\right)\end{array}\right]\end{array}\right)}\\ =\sqrt{\left[\begin{array}{l}\left[{\left(\left(-0.20\right)-0.0820\right)}^2\times 0.25\right]+\left[{\left(0.12-0.0820\right)}^2\times 0.60\right]\\ +\left[{\left(0.40-0.0820\right)}^2\times 0.15\right]\end{array}\right]}\\ =\sqrt{\left({\left(-0.282\right)}^2\times 0.25\right)+\left({\left(0.038\right)}^2\times 0.60\right)+\left({\left(0.318\right)}^2\times 0.15\right)}\\ =\sqrt{\left(0.079524\times 0.25\right)+\left(0.001444\times 0.60\right)+\left(0.101124\times 0.15\right)}\end{array}$

$\begin{array}{c}=\sqrt{\left(0.019881+0.0008664+0.0151686\right)}\\ =\sqrt{0.035916}\\ =0.1895\end{array}$

Hence, the standard deviation of Stock II is 0.1895 or 18.95%.

Interpretation:

The beta refers to the systematic risk of the stock. Stock I has higher beta than Stock II. Hence, the systematic risk of Stock I is higher.

The standard deviation indicates the total risk of the stock. The standard deviation is high for Stock II despite having a low beta. Hence, a major portion of the standard deviation of Stock II is the unsystematic risk. Therefore, Stock II has higher unsystematic risk than Stock I.

Summary Introduction

To discuss: The riskier Stock among Stock I and Stock II.

Introduction:

Risk refers to the movement or fluctuation in the value of an investment. The movement can be positive or negative. A positive fluctuation in the price benefits the investor. The investor will lose money if the price movement is negative.

Explanation of Solution

The formation of a portfolio helps in diversifying the unsystematic risk. Although, the Stock II has a higher unsystematic risk, it can be diversified completely. However, the beta cannot be eliminated. Hence, the Stock I is riskier than Stock II.