
Precalculus Plus MyLab Math with eText -- Access Card Package (10th Edition) (Sullivan & Sullivan Precalculus Titles)
10th Edition
ISBN: 9780321978981
Author: Michael Sullivan
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 1.1, Problem 20AYU
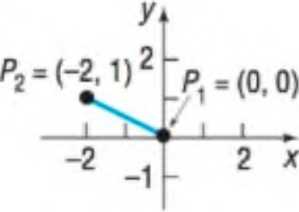
In Problems 35-46, find the distance between the points and .
36.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
a
->
f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem)
Muslim_maths
Use Green's Theorem to evaluate F. dr, where
F = (√+4y, 2x + √√)
and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to
(0,0).
Evaluate
F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line
π 1
1
segment starting at the point (8,
'
and ending at the point (3,
2
3'6
Chapter 1 Solutions
Precalculus Plus MyLab Math with eText -- Access Card Package (10th Edition) (Sullivan & Sullivan Precalculus Titles)
Ch. 1.1 - 1. On a real number line the origin is assigned...Ch. 1.1 - 2. If 3 and 5 are the coordinates of two points on...Ch. 1.1 - 3. If 3 and 4 are the legs of a right triangle,...Ch. 1.1 - 4. Use the converse of the Pythagorean Theorem to...Ch. 1.1 - 5. The area of a triangle whose base is b and...Ch. 1.1 - 6. True or False Two triangles are congruent if...Ch. 1.1 - 7. If ( x,y ) are the coordinates of a point P in...Ch. 1.1 - 8. The coordinate axes divide the xy-plane into...Ch. 1.1 - 9. If three distinct points P , Q and R all lie on...Ch. 1.1 - 10. True or False The distance between two points...
Ch. 1.1 - 11. True or False The point (1,4) lies in quadrant...Ch. 1.1 - 12. True or False The midpoint of a line segment...Ch. 1.1 - Multiple Choice Which of the following statements...Ch. 1.1 - Multiple Choice Choose the expression that equals...Ch. 1.1 - In Problems 15 and 16, plot each point in the...Ch. 1.1 - In Problems 15 and 16, plot each point in the...Ch. 1.1 - 17. Plot the points ( 2,0 ),( 2,3 ),( 2,4 ),(2,1)...Ch. 1.1 - 18. Plot the points ( 0,3 ),( 1,3 ),( 2,3 ),(5,3)...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 19-30, find the distance d(P1,P2)...Ch. 1.1 - In Problem 1932 find the distance d between the...Ch. 1.1 - In Problems 19-30, find the distance between the...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - A suitable restriction on the domain of the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 3744, find the midpoint of the line...Ch. 1.1 - In Problems 3946 find the midpoint of the line...Ch. 1.1 - In problems find the midpoint of the line segment...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - If the point (2,5) is shifted 3 units to the right...Ch. 1.1 - If the point (1,6) is shifted 2 units to the left...Ch. 1.1 - Find all points having an-coordinate ofwhose...Ch. 1.1 - Find all points having a-coordinate ofwhose...Ch. 1.1 - Find all points on the x-axis that are 6 units...Ch. 1.1 - Find all points on the-axis that areunits from the...Ch. 1.1 - Suppose thatare the coordinates of a point in...Ch. 1.1 - Plot the pointsandin the-plane. Ifis the midpoint...Ch. 1.1 - The midpoint of the line segment from P1 to P2 is...Ch. 1.1 - Geometry Verify that the points (0,0),(a,0) and...Ch. 1.1 - The medians of a triangle are the line segments...Ch. 1.1 - An equilateral triangle is one in which all three...Ch. 1.1 - Geometry Find the midpoint of each diagonal of a...Ch. 1.1 - 67. Distance between Moving Objects A Ford Focus...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - Baseball A major league baseball “diamond� is...Ch. 1.1 - Little league Baseball The layout of a Little...Ch. 1.1 - Baseball Refer to Problem 63. Overlay a...Ch. 1.1 - Little league Baseball Refer to Problem 64....Ch. 1.1 - 67. Distance between Moving Objects A Ford Focus...Ch. 1.1 - Distance of a Moving Object from a Fixed Point A...Ch. 1.1 - Drafting Error When a draftsman draws three lines...Ch. 1.1 - Net Sales The figure on page 9 illustrates how net...Ch. 1.1 - Poverty Threshold Poverty thresholds are...Ch. 1.1 - Write a paragraph that describes a Cartesian...Ch. 1.2 - Solve: 2( x+3 )1=7 (pp. A44-A46)Ch. 1.2 - Solve the equation x29=0Ch. 1.2 - The points, if any, at which a graph crosses or...Ch. 1.2 - The -intercepts of the graph of an equation are...Ch. 1.2 - Prob. 5AYUCh. 1.2 - Prob. 6AYUCh. 1.2 - Prob. 7AYUCh. 1.2 - True or False To find the y-intercepts of the...Ch. 1.2 - True or False The-coordinate of a point at which...Ch. 1.2 - True or False If a graph is symmetric with respect...Ch. 1.2 - Multiple Choice Given that the intercepts of a...Ch. 1.2 - To test whether the graph of an equation is...Ch. 1.2 - In Problems, determine which of the given points...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems, determine which of the given points...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems , find the intercepts and graph each...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - Prob. 53AYUCh. 1.2 - Prob. 54AYUCh. 1.2 - Prob. 55AYUCh. 1.2 - Prob. 56AYUCh. 1.2 - Prob. 57AYUCh. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 5772, list the intercepts and test for...Ch. 1.2 - In Problems 5772, list the intercepts and test for...Ch. 1.2 - Prob. 63AYUCh. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - Prob. 65AYUCh. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - Prob. 67AYUCh. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - Prob. 69AYUCh. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - If (a,4) is a point on the graph of y= x 2 +3x ,...Ch. 1.2 - Prob. 79AYUCh. 1.2 - If the graph of an equation is symmetric with...Ch. 1.2 - If the graph of an equation is symmetric with...Ch. 1.2 - If the graph of an equation is symmetric with...Ch. 1.2 - Microphones n studios and on stages, cardioid...Ch. 1.2 - Solar Energy The solar electric generating systems...Ch. 1.2 -
Graph,,and,noting which graphs are the...Ch. 1.2 - Explain what is meant by a complete graph.Ch. 1.2 - Draw a graph of an equation that contains two...Ch. 1.2 - Make up an equation with the intercepts,and....Ch. 1.2 - Draw a graph that contains the points ( 2,1 ) , (...Ch. 1.2 - Prob. 90AYUCh. 1.2 - Draw a graph that contains the points ( 2,5 ) , (...Ch. 1.3 - The slope of a vertical line is ______; the slope...Ch. 1.3 - For the line 2x+3y=6 , the x-intercept is ______...Ch. 1.3 - True or False The equation 3x+4y=6 is written in...Ch. 1.3 - True or False The slope of the line 2y=3x+5 is 3.Ch. 1.3 - True or False The point ( 1,2 ) is on the line...Ch. 1.3 - Two nonvertical lines have slopes m 1 ,and m 2 ,...Ch. 1.3 - The lines y=2x+3andy=ax+5 are parallel if a=...Ch. 1.3 - The lines y=2x1andy=ax+2 are perpendicular if...Ch. 1.3 - True or False Perpendicular lines have slopes that...Ch. 1.3 - If a line slants downward from left to right, then...Ch. 1.3 - Choose the formula for finding the slope m of a...Ch. 1.3 - Choose the correct statement about the graph of...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 33-38, the slope and a point on a line...Ch. 1.3 - In Problems 33-38, the slope and a point on a line...Ch. 1.3 - In Problems 33-38, the slope and a point on a line...Ch. 1.3 - In Problems 33-38, the slope and a point on a line...Ch. 1.3 - In Problems 33-38, the slope and a point on a line...Ch. 1.3 - In Problems 33-38, the slope and a point on a line...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 7998, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 7998, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - Find an equation of the x-axis .Ch. 1.3 - Find an equation of the y-axis .Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems, write an equation of each line....Ch. 1.3 - In Problems 115118, write an equation of each...Ch. 1.3 - In Problems 115118, write an equation of each...Ch. 1.3 - In Problems, write an equation of each line....Ch. 1.3 - Geometry Use slopes to show that the triangle...Ch. 1.3 - Geometry Use slopes to show that the quadrilateral...Ch. 1.3 - Geometry Use slopes to show that the quadrilateral...Ch. 1.3 - Geometry Use slopes and the distance formula to...Ch. 1.3 - Geometry Truck Rentals A truck rental company...Ch. 1.3 -
Cost Equation The Fixed costs of operating a...Ch. 1.3 -
Cost of Driving a Car The annual fixed costs...Ch. 1.3 - Wages of a Car Salesperson Dan receives 375 per...Ch. 1.3 - Electricity Rates in IIIinois Commonwealth Edison...Ch. 1.3 - Electricity Rates in Florida Florida Power Light...Ch. 1.3 - Measuring Temperature The relationship between...Ch. 1.3 - Measuring Temperature The Kelvin scale for...Ch. 1.3 - Access Ramp A wooden access ramp is being built...Ch. 1.3 -
. Cigarette Use A report in the Child Trends...Ch. 1.3 - Prob. 127AYUCh. 1.3 - The equation 2xy=C defines a family of lines, one...Ch. 1.3 - Show that the line containing the points ( a,b...Ch. 1.3 - Prove that if two nonvertical lines have slopes...Ch. 1.3 - Prob. 131AYUCh. 1.3 - Which of the following equations might have the...Ch. 1.3 - Prob. 133AYUCh. 1.3 - Prob. 134AYUCh. 1.3 - Prob. 135AYUCh. 1.3 - Prob. 136AYUCh. 1.3 - Carpentry Carpenters use the term pitch to...Ch. 1.3 - Prob. 138AYUCh. 1.3 - Prob. 139AYUCh. 1.3 - What can you say about two lines that have equal...Ch. 1.3 - Prob. 141AYUCh. 1.3 - Prob. 142AYUCh. 1.3 - Prob. 143AYUCh. 1.3 - Prob. 144AYUCh. 1.3 - Prob. 145AYUCh. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - 5. List the intercepts of the following graph.Ch. 1.4 - 6. Graph y= x 2 +15 using a graphing utility....Ch. 1.4 - Prob. 7AYUCh. 1.4 - Prob. 8AYUCh. 1.4 - Prob. 9AYUCh. 1.4 - Prob. 10AYUCh. 1.4 - Prob. 11AYUCh. 1.4 - Prob. 12AYUCh. 1.4 - Prob. 13AYUCh. 1.4 - Prob. 14AYUCh. 1.4 - Prob. 15AYUCh. 1.4 - Prob. 16AYUCh. 1.4 - Prob. 17AYUCh. 1.4 - Prob. 18AYUCh. 1.4 - Prob. 19AYUCh. 1.4 - Prob. 20AYUCh. 1.4 - Prob. 21AYUCh. 1.4 - Prob. 22AYUCh. 1.4 - Prob. 23AYUCh. 1.4 - Prob. 24AYUCh. 1.4 - Prob. 25AYUCh. 1.4 - Prob. 26AYUCh. 1.4 - Prob. 27AYUCh. 1.4 - Prob. 28AYUCh. 1.4 - Prob. 29AYUCh. 1.4 - Prob. 30AYUCh. 1.4 - Prob. 31AYUCh. 1.4 - Prob. 32AYUCh. 1.4 - Prob. 33AYUCh. 1.4 - Prob. 34AYUCh. 1.4 - Prob. 35AYUCh. 1.4 - Prob. 36AYUCh. 1.4 - Prob. 37AYUCh. 1.4 - Prob. 38AYUCh. 1.4 - Prob. 39AYUCh. 1.4 - Prob. 40AYUCh. 1.4 - Prob. 41AYUCh. 1.4 - Prob. 42AYUCh. 1.4 - Prob. 43AYUCh. 1.4 - Prob. 44AYUCh. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - 58. Find an equation of the line containing the...Ch. 1.4 - 49. Find the area of the square in the figure.Ch. 1.4 - 50. Find the area of the blue shaded region in the...Ch. 1.4 - Prob. 51AYUCh. 1.4 - Prob. 52AYUCh. 1.4 - Weather Satellites Earth is represented on a map...Ch. 1.4 - 54. The tangent line to a circle may be defined as...Ch. 1.4 - 57. Refer to Problem 54. The line x2y+4=0 is...Ch. 1.4 - 55. The Greek Method the Greek method for finding...Ch. 1.4 - 56. Use the Greek method described in Problem 55...Ch. 1.4 - Prob. 59AYUCh. 1.4 - If the circumference of a circle is 6, what is its...Ch. 1.4 - 61. Which of the following equations might have...Ch. 1.4 - 62. Which of the following equations might have...Ch. 1.4 - 63. Explain how the center and radius of a circle...Ch. 1.4 - Prob. 64AYUCh. 1 - In Problems 1-4, find the following for each pair...Ch. 1 - In Problems 1-4, find the following for each pair...Ch. 1 - In Problems 1-4, find the following for each pair...Ch. 1 - Graph by plotting points.
Ch. 1 - List the intercepts of the following graph.Ch. 1 - In Problems 10-14, test each equation for symmetry...Ch. 1 - In Problems 10-14, test each equation for symmetry...Ch. 1 - In problems , list the intercepts and test for...Ch. 1 - In Problems 10-14, test each equation for symmetry...Ch. 1 - In Problems 10-14, test each equation for symmetry...Ch. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - In problems , Finf the center and radius of each...Ch. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - In Problems 18-25, find an equation of the line...Ch. 1 - In Problems 18-25, find an equation of the line...Ch. 1 - y-intercept=2 ; containing the point ( 5,3 )Ch. 1 - Containing the points ( 3,4 ) and ( 2,1 )Ch. 1 - Parallel to the line 2x3y=4 ; containing the point...Ch. 1 - In problems , Find an equation of the line having...Ch. 1 - In problems 22 and 23, Find the slope and...Ch. 1 - In problems and , Find the slope and -intercept...Ch. 1 - In problems 24 and 25, Find the interceptsand...Ch. 1 - In problems 24 and 25, Find the interceptsand...Ch. 1 - Sketch a graph of y= x 3 .Ch. 1 - Graph y=x.Ch. 1 - 35. Graph the line with slope 2 3 containing the...Ch. 1 - Show that the points A=(3,4),B=(1,1), and C=(2,3)...Ch. 1 - Show that the points A=( 2,0 ) , B=( 4,4 ) , and...Ch. 1 - Prob. 31RECh. 1 - 31. Show that the points A=( 2,5 ) , B=( 6,1 ) ,...Ch. 1 - In Problems , use and .
Find the distance from ...Ch. 1 - In Problems , use and .
Find the midpoint of...Ch. 1 - In Problems , use and .
(a) Find the slope of...Ch. 1 - In Problems , use and .
Graph by plotting...Ch. 1 - In Problems , use and .
Graph .
Ch. 1 - In Problems , use and .
List the intercepts and...Ch. 1 - In Problems , use and .
Write the...Ch. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - In Problems 13, use P1=(1,3) and P2=(5,1). For the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Hypothesis Testing Using a P-Value In Exercises 31–36,
identify the claim and state H0 and Ha.
find the standar...
Elementary Statistics: Picturing the World (7th Edition)
CHECK POINT I You deposit $1000 in a saving account at a bank that has a rate of 4%. a. Find the amount, A, of ...
Thinking Mathematically (6th Edition)
Critical Values. In Exercises 41–44, find the indicated critical value. Round results to two decimal places.
43...
Elementary Statistics (13th Edition)
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
Women’s Heights Assume that college women’s heights are approximately Normally distributed with a mean of 65 in...
Introductory Statistics
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- I need help in ensuring that I explain it propleryy in the simplifest way as possiblearrow_forwardI need help making sure that I explain this part accutartly.arrow_forwardPlease help me with this question as I want to know how can I perform the partial fraction decompostion on this alebgric equation to find the time-domain of y(t)arrow_forward
- Please help me with this question as I want to know how can I perform the partial fraction on this alebgric equation to find the time-domain of y(t)arrow_forwardEvaluate F³ - dr where ♬ = (4z, -4y, x), and C' is given by (t) = (sin(t), t, cos(t)), 0≤t≤ñ .arrow_forwardMid-Term Review Find the formula for (f + g)(x). f(x) = x² - 10x + 25 and g(x) = x² - 10x + 24 (f + g) (x) = [ 2 ]x² X + DELL Skip Sarrow_forward
- Calculus III May I please have some elaborations on Example 2 part a? Thank you.arrow_forward1. A bicyclist is riding their bike along the Chicago Lakefront Trail. The velocity (in feet per second) of the bicyclist is recorded below. Use (a) Simpson's Rule, and (b) the Trapezoidal Rule to estimate the total distance the bicyclist traveled during the 8-second period. t 0 2 4 6 8 V 10 15 12 10 16 2. Find the midpoint rule approximation for (a) n = 4 +5 x²dx using n subintervals. 1° 2 (b) n = 8 36 32 28 36 32 28 24 24 20 20 16 16 12 8- 4 1 2 3 4 5 6 12 8 4 1 2 3 4 5 6arrow_forward= 5 37 A 4 8 0.5 06 9arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning 
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning


Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Implicit Differentiation Explained - Product Rule, Quotient & Chain Rule - Calculus; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=LGY-DjFsALc;License: Standard YouTube License, CC-BY