Chapter 11, Problem 1E

To determine

The nonisomorphic graphs of order 1, order 2 and order 3, and explain why the answer is $\infty$ for general graphs.

Answer to Problem 1E

The number nonisomorphic graphs of order 1 is $\underset{\_}{1}$, of order 2 is $\underset{\_}{2}$ and of order 3 is $\underset{\_}{4}$.

Explanation of Solution

Definition used:

“Two general graphs $G=\left(V,E\right)$ and $G=\left(V^{\prime },E^{\prime }\right)$ are called isomorphic, provided that there is a one-to-one correspondence $\theta :V\to V^{\prime }$ between their vertex sets such that, for each pair of vertices x and y of V, there are as many edges of G joining x and y as there are edges of $G^{\prime }$ joining $\theta \left(x\right)\text{ and }\theta \left(y\right)$. The one-to-one correspondence $\theta$ is called an isomorphism of G and $G^{\prime }$.”

Calculation:

By the definition of the isomorphic graphs, it is observed that the two graphs will have same number of vertices and edges having structural similarities.

Consider the case when order of a simple graph is 1. This graph will have exactly 1 vertex.

The only possible simple graph of order 1 is the graph with one vertex having no edge, which is shown below in Figure 1.

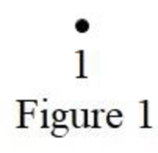
From Figure 1, it is observed that the number of nonisomorphic graphs of order 1 is $\underset{\_}{1}$.

Consider the case when order of a simple graph is 2. This graph will have exactly 2 vertex.

The only possible simple graphs of order 2 is the graph with two vertex having no edge as well as one edge, which is shown below in Figure 2.

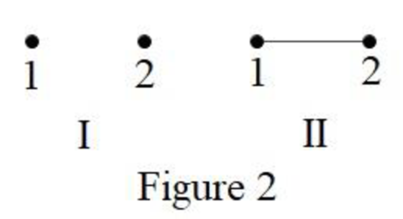
From Figure 2, it is observed that the graphs I and II are nonisomorphic.

Therefore, the number of nonisomorphic graphs of order 2 is $\underset{\_}{2}$.

Consider the case when order of a simple graph is 3. This graph will have exactly 3 vertex.

There are 7 possible simple graphs of order 3, which is shown below in Figure 3.

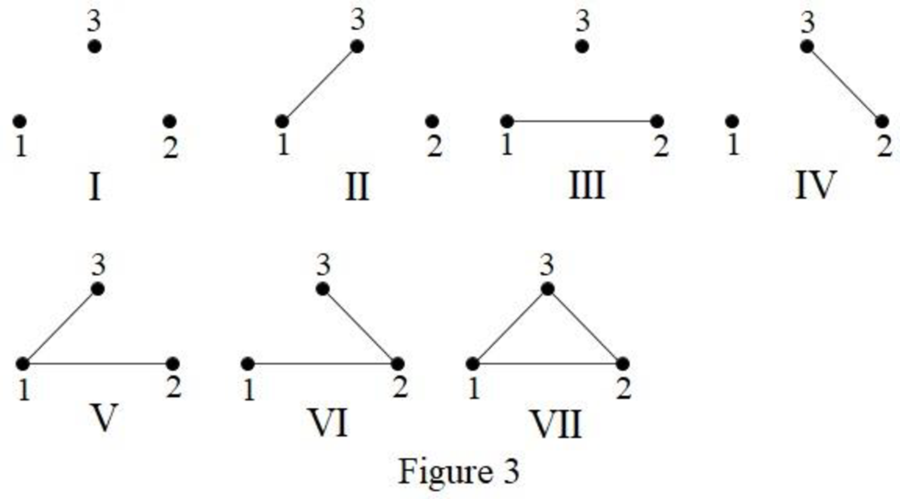
From Figure 3, it is observed that the graphs II, III and IV are isomorphic.

Also, the graphs V and VI are isomorphic.

Thus, the nonisomorphic graphs of order 3 are I, II, V and VII which has the number of edges 0, 1, 2 and 3, respectively.

Therefore, the number nonisomorphic graphs of order 3 is $\underset{\_}{4}$.

In the case of general graphs, loops and multi-edges will be present.

That is, for general graphs there is no bound on the number of edges irrespective of the order. Even a single vertex may have many loops.

For example, consider the graph shown below in Figure 4.

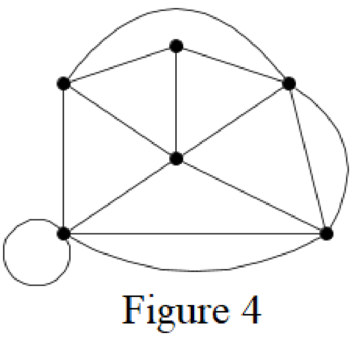
The graph in Figure 4 has multiple edges and loops. There can be many more loops and multiple edges possible in the same graph.

It is known that a graph of order n can have n loops, $n\left(n-1\right)$ edges and as many multi-edges.

Thus, for general graphs, the number of nonisomorphic graphs of order n will be infinite.