
Concept explainers
A quantitative measure of how efficiently spheres pack into unit cells is called packing efficiency, which is the percentage of the cell space occupied by the spheres. Calculate the packing efficiencies of a simple cubic cell, a body-centered cubic cell, and a face-centered cubic cell. (Hint: Refer to Figure 11.22 and use the relationship that the volume of a sphere is
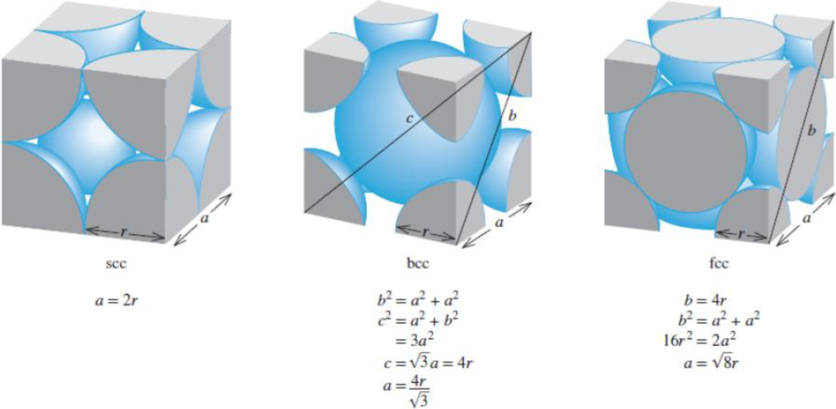
Figure 11.22 The relationship between the edge length (a) and radius (r) of atoms in the simple cubic cell, body-centered cubic cell, and face-centered cubic cell.
Interpretation: Packing efficiency of a simple cubic cell, body-centred cubic and face-centred cubic unit cells, have to be calculated.
Concept Introduction:
The major types of cubic unit cells are:
- Simple cubic unit cell.
- Face-centered cubic unit cell.
- Body-centered cubic unit cell.
Packing efficiency, is the percentage of the cell space occupied by the spheres in a cubic unit cell of any type. The atoms in the unit cells are considered as spheres.
Answer to Problem 11.134QP
The packing efficiency of a simple cubic unit cell is
The packing efficiency of a body-centred cubic unit cell is
The packing efficiency of a face-centered cubic unit cell is
Explanation of Solution
Calculating the packing efficiency for a simple cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the simple cubic unit cell is 1.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the simple cubic unit cell can be expressed as:
Thus, the packing efficiency of a simple cubic unit cell is
Calculating the packing efficiency for a body-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 2.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a body-centered cubic unit cell is
Calculating the packing efficiency for a face-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 4.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a face-centered cubic unit cell is
Using figure 11.2 as reference, the packing efficiency for the different types of cubic unit cells have been calculated.
Want to see more full solutions like this?
Chapter 11 Solutions
AVC LOOSELEAF CHEMISTRY W/CONNECT 2 SEM
- Calculating the pH at equivalence of a titration 3/5 Izabella A chemist titrates 120.0 mL of a 0.7191M dimethylamine ((CH3)2NH) solution with 0.5501 M HBr solution at 25 °C. Calculate the pH at equivalence. The pk of dimethylamine is 3.27. Round your answer to 2 decimal places. Note for advanced students: you may assume the total volume of the solution equals the initial volume plus the volume of HBr solution added. pH = ☐ ✓ 18 Ar Boarrow_forwardAlcohols can be synthesized using an acid-catalyzed hydration of an alkene. An alkene is combined with aqueous acid (e.. sulfuric acid in water). The reaction mechanism typically involves a carbocation intermediate. > 3rd attempt 3343 10 8 Draw arrows to show the reaction between the alkene and hydronium ion. that 2nd attempt Feedback 1st attempt تعمال Ju See Periodic Table See Hint F D Ju See Periodic Table See Hintarrow_forwardDraw the simplified curved arrow mechanism for the reaction of acetone and CHgLi to give the major product. 4th attempt Π Draw the simplified curved arrow mechanism T 3rd attempt Feedback Ju See Periodic Table See Hint H -H H -I H F See Periodic Table See Hintarrow_forward
- Select the correct reagent to accomplish the first step of this reaction. Then draw a mechanism on the Grignard reagent using curved arrow notation to show how it is converted to the final product. 4th attempt Part 1 (0.5 point) Select the correct reagent to accomplish the first step of this reaction. Choose one: OA Mg in ethanol (EtOH) OB. 2 Li in THF O C. Li in THF D. Mg in THF O E Mg in H2O Part 2 (0.5 point) Br Part 1 Bri Mg CH B CH, 1 Draw intermediate here, but no arrows. © TE See Periodic Table See Hint See Hint ין Harrow_forwardSelect the product for the following reaction. HO HO PCC OH ○ OH O HO ○ HO HO HOarrow_forward5:45 Х Select the final product for the following reaction sequence. O O 1. Mg. ether 2.D.Oarrow_forward
- Based on the chart Two similarities between the molecule with alpha glycosidic linkages. Two similarities between the molecules with beta glycosidtic linkages. Two differences between the alpha and beta glycosidic linkages.arrow_forwardplease help fill in the tablearrow_forwardAnswer F pleasearrow_forward
- 4. Refer to the data below to answer the following questions: The octapeptide saralasin is a specific antagonist of angiotensin II. A derivative of saralasin is used therapeutically as an antihypertensive. Amino acid analysis of saralasin show the presence of the following amino acids: Ala, Arg, His, Pro, Sar, Tyr, Val, Val A.Sar is the abbreviation for sarcosine, N-methyl aminoethanoic acid. Draw the structure of sarcosine. B. N-Terminal analysis by the Edman method shows saralasin contains sarcosine at the N-terminus. Partial hydrolysis of saralasin with dilute hydrochloric acid yields the following fragments: Tyr-Val-His Sar-Arg-Val His-Pro-Ala Val-Tyr-Val Arg-Val-Tyr What is the structure of saralasin?arrow_forwardWhat is the structure of the DNA backbone?arrow_forwardPLEASE PLEASE PLEASE use hand drawn structures when possarrow_forward
 General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning





