Explanation Given: First three Steps of generation of quadratic Koch Curve as below- Formula used: Fractal dimension D of the object is found from N = R D Where, N is the factor by which number of element increases when ruler is shortened by a factor R. Taking logarithm on both the sides- log(N) = log(R D ) log(N) = D log(R) [applying the rule log(a x ) = x log(a) to right hand side] D = log ( N ) log ( R ) An object is defined as fractal if it has a non-integer dimension. Calculation: a. It can be observed from the steps of quadratic Koch curve generation- For R = 1, N = 1 = 1 3 2 For R = 4,N = 8 = 4 3 2 For R = 16, N = 8 × 8 = 64 = 16 3 2 Thus, in general, N = R 3 2 b. Fractal dimension = log ( N ) log ( R ) = 3 2 = 1.5 In every step of the quadratic Koch curve generation ruler size is reduced by a factor of 4 and the number of elements increases by factor of 8...

Using & Understanding Mathematics, Books a la Carte edition (7th Edition)

7th Edition

ISBN: 9780134716015

Author: Jeffrey O. Bennett, William L. Briggs

Publisher: PEARSON

See similar textbooks

Concept explainers

Family of Curves

A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These…

XZ Plane

In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are…

Euclidean Geometry

Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) ge…

Lines and Angles

In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.

Videos

Question

Chapter 10.C, Problem 27E

To determine

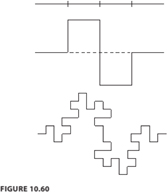
a. The relation between N and R for quadratic Koch curve.

b. The fractal dimension of quadratic coach curve and conclusion about the length of quadratic Koch curve with conclusions

c. Why the total area of quadratic Koch Island is the same as the area of the original square and the length of the Koch Island.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 10.C, Problem 26E

Chapter 10.C, Problem 28E

Students have asked these similar questions

In a volatile housing market, the overall value of a home can be modeled by V(x) = 415x² - 4600x + 200000, where V represents the value of the home and x represents each year after 2020. Part A: Find the vertex of V(x). Show all work. Part B: Interpret what the vertex means in terms of the value of the home.

Show all work to solve 3x² + 5x - 2 = 0.

Two functions are given below: f(x) and h(x). State the axis of symmetry for each function and explain how to find it. f(x) h(x) 21 5 4+ 3 f(x) = −2(x − 4)² +2 + -5 -4-3-2-1 1 2 3 4 5 -1 -2 -3 5

Chapter 10 Solutions

Using & Understanding Mathematics, Books a la Carte edition (7th Edition)

Ch. 10.A - Prob. 1QQ Ch. 10.A - Prob. 2QQ Ch. 10.A - An acute angle is a. less than 90°. b. exactly...Ch. 10.A - 4. A regular polygon always has a. four sides. b....Ch. 10.A - 5. A right triangle always has three equal-length...Ch. 10.A - 6. The circumference of a circle of radius r...Ch. 10.A - The volume of a sphere of radius r is a. \[\pi...Ch. 10.A - Prob. 8QQ Ch. 10.A - If you triple the radius of a sphere, the volume...Ch. 10.A - Suppose you cut a large stone block into four...

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.