
Calculus, Early Transcendentals
7th Edition
ISBN: 9780131569898
Author: C. Henry Edwards, David E. Penney
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10.5, Problem 30E
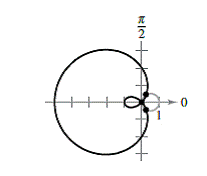
Finding Points of Intersection In Exercises 27-34, find the points of intersection of the graphs of the equations.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
5. The graph of ƒ is given below. Sketch a graph of f'.
6. The graph of ƒ is given below. Sketch a graph of f'.
0
x
7. The graph of ƒ is given below. List the x-values where f is not differentiable.
0
A
2
4
2. DRAW a picture, label using variables to represent each component, set up an
equation to relate the variables, then differentiate the equation to solve the
problem below.
The top of a ladder slides down a vertical wall at a rate of 0.15 m/s. At the moment when the
bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s. How
long is the ladder?
Please answer all questions and show full credit please
Chapter 10 Solutions
Calculus, Early Transcendentals
Ch. 10.1 - Conic Sections State the definitions of parabola,...Ch. 10.1 - Reflective Property Use a sketch to illustrate the...Ch. 10.1 - Eccentricity Consider an ellipse with eccentricity...Ch. 10.1 - Prob. 4ECh. 10.1 - Match the following graph with its equations y2=4x...Ch. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - Find the vertex, focus and directrix of the...Ch. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Find the vertex, focus and directrix of the...Ch. 10.1 - Prob. 16ECh. 10.1 - Finding the Standard Equation of a Parabola In...Ch. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Find the standard form -of the...Ch. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Find the standard form -of the...Ch. 10.1 - Prob. 24ECh. 10.1 - Find the centre, foci, vertices, eccentricity of...Ch. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Finding the Standard Equation of an Ellipse In...Ch. 10.1 - Find the equation of the ellipse with the given...Ch. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Find the center, foci, vertices and eccentricity...Ch. 10.1 - Prob. 40ECh. 10.1 - Find the standard form of equation of hyperbola...Ch. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Find the equation for tangent and normal to the...Ch. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Classifying the Graph of an Equation In Exercises...Ch. 10.1 - Prob. 53ECh. 10.1 - Prob. 54ECh. 10.1 - Classifying the Graph of an Equation In Exercises...Ch. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Prob. 59ECh. 10.1 - HOW DO YOU SEE IT? Describe in words how a plane...Ch. 10.1 - Prob. 61ECh. 10.1 - Beam Deflection A simply supported beam that is 16...Ch. 10.1 - Prob. 63ECh. 10.1 - Prob. 64ECh. 10.1 - Prob. 65ECh. 10.1 - Prob. 66ECh. 10.1 - Architecture A church window is bounded above by a...Ch. 10.1 - Prob. 68ECh. 10.1 - Prob. 69ECh. 10.1 - Prob. 70ECh. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.1 - Prob. 75ECh. 10.1 - Prob. 76ECh. 10.1 - Arc Length Use the integration capabilities of a...Ch. 10.1 - Prob. 78ECh. 10.1 - Prob. 79ECh. 10.1 - Proof Prove Theorem 10.4 by showing that the...Ch. 10.1 - Prob. 81ECh. 10.1 - Hyperbola Consider a hyperbola centered at the...Ch. 10.1 - Navigation LORAN (long distance radio navigation)...Ch. 10.1 - Hyperbolic Mirror A hyperbolic mirror (used in...Ch. 10.1 - Prob. 85ECh. 10.1 - Prob. 86ECh. 10.1 - Prob. 87ECh. 10.1 - Prob. 88ECh. 10.1 - Prob. 89ECh. 10.1 - Determine whether the following statement is true...Ch. 10.1 - Prob. 91ECh. 10.1 - Prob. 92ECh. 10.1 - For a point P on an ellipse, let d be the distance...Ch. 10.1 - Prob. 94ECh. 10.2 - Parametric Equations What information does a set...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Sketch the curve represented 'by -the following...Ch. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Eliminate the parameter and obtain the rectangular...Ch. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 48ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 50ECh. 10.2 - Finding Parametric Equations In Exercises 51-54,...Ch. 10.2 - Finding Parametric Equations In Exercises 51-54,...Ch. 10.2 - Finding Parametric Equations In Exercises 51-54,...Ch. 10.2 - Finding Parametric Equations In Exercises 51-54,...Ch. 10.2 - Find the set of parametric equations that...Ch. 10.2 - Find the set of parametric equations that...Ch. 10.2 - Find the set of parametric equations that...Ch. 10.2 - Find the set of parametric equations that...Ch. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - Prob. 61ECh. 10.2 - Prob. 62ECh. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Prob. 66ECh. 10.2 - Prob. 67ECh. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Match the set of parametric equation with the...Ch. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - Prob. 74ECh. 10.2 - Prob. 75ECh. 10.2 - Epicycloid A circle of radius 1 rolls around the...Ch. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - Prob. 79ECh. 10.2 - Prob. 80ECh. 10.2 - Baseball The center field fence in a ballpark is...Ch. 10.2 - Prob. 82ECh. 10.3 - Parametric Form of the Derivative What does the...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Arc Length Why does the arc length formula require...Ch. 10.3 - Finding a Derivative In Exercises 5-8, find dy/dx....Ch. 10.3 - Finding a Derivative x=t3,y=4tCh. 10.3 - Finding a Derivative dy/dx x=sin2,y=cos2Ch. 10.3 - Finding a Derivative dy/dx. x=2e,y=e/2Ch. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 10.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 10.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Horizontal and Vertical Tangency In Exercises...Ch. 10.3 - Prob. 34ECh. 10.3 - Horizontal and Vertical Tangency In Exercises...Ch. 10.3 - Horizontal and Vertical Tangency In Exercises...Ch. 10.3 - Horizontal and Vertical Tangency In Exercises...Ch. 10.3 - Horizontal and Vertical Tangency In Exercises...Ch. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Prob. 55ECh. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Prob. 61ECh. 10.3 - Prob. 62ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 67ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 69ECh. 10.3 - Prob. 70ECh. 10.3 - Prob. 71ECh. 10.3 - Surface Area In Exercises 69-72, write an integral...Ch. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - HOW DO YOU SEE IT? Using the graph of /. (a)...Ch. 10.3 - Integration by Substitution Use integration by...Ch. 10.3 - Prob. 78ECh. 10.3 - Area In Exercises 79 and 80. find the area of the...Ch. 10.3 - Prob. 80ECh. 10.3 - Prob. 81ECh. 10.3 - Prob. 82ECh. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Centroid In Exercises 87 and 88. find the centroid...Ch. 10.3 - Centroid In Exercises 87 and 88. find the centroid...Ch. 10.3 - Volume In Exercises 89 and 90, find the volume of...Ch. 10.3 - Prob. 90ECh. 10.3 - Prob. 91ECh. 10.3 - Prob. 92ECh. 10.3 - Prob. 93ECh. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - Prob. 96ECh. 10.3 - Prob. 97ECh. 10.3 - Prob. 98ECh. 10.3 - Prob. 99ECh. 10.3 - Prob. 100ECh. 10.4 - Polar Coordinates Consider the polar coordinates...Ch. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Prob. 8ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Prob. 12ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises 5-14,...Ch. 10.4 - Prob. 14ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 26ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 28ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 30ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 32ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 34ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 36ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 42ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Prob. 59ECh. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.4 - Prob. 67ECh. 10.4 - Prob. 68ECh. 10.4 - Prob. 69ECh. 10.4 - Prob. 70ECh. 10.4 - Prob. 71ECh. 10.4 - Prob. 72ECh. 10.4 - Prob. 73ECh. 10.4 - Prob. 74ECh. 10.4 - Prob. 75ECh. 10.4 - Prob. 76ECh. 10.4 - Prob. 77ECh. 10.4 - Prob. 78ECh. 10.4 - Prob. 79ECh. 10.4 - Prob. 80ECh. 10.4 - Prob. 81ECh. 10.4 - Prob. 82ECh. 10.4 - Prob. 83ECh. 10.4 - Prob. 84ECh. 10.4 - Prob. 85ECh. 10.4 - Prob. 86ECh. 10.4 - Prob. 87ECh. 10.4 - Prob. 88ECh. 10.4 - Prob. 89ECh. 10.4 - Prob. 90ECh. 10.4 - Prob. 91ECh. 10.4 - Prob. 92ECh. 10.4 - Prob. 93ECh. 10.4 - Prob. 94ECh. 10.4 - Prob. 95ECh. 10.4 - Asymptote In Exercises 95-96, use a graphing...Ch. 10.4 - Prob. 97ECh. 10.4 - Prob. 98ECh. 10.4 - Prob. 99ECh. 10.4 - Prob. 100ECh. 10.4 - Prob. 101ECh. 10.4 - Prob. 102ECh. 10.4 - Rotated Curve In Exercises 103-105, use the...Ch. 10.4 - Prob. 104ECh. 10.4 - Prob. 105ECh. 10.4 - Prob. 106ECh. 10.4 - Prob. 107ECh. 10.4 - Prob. 108ECh. 10.4 - Prob. 109ECh. 10.4 - Prob. 110ECh. 10.4 - Prob. 111ECh. 10.4 - Prob. 112ECh. 10.4 - Prob. 113ECh. 10.4 - Prob. 114ECh. 10.4 - Prob. 115ECh. 10.4 - Prob. 116ECh. 10.5 - Area of a Polar Region What should you check...Ch. 10.5 - Prob. 2ECh. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 8ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 12ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Finding the Area of a Polar Region In Exerdses...Ch. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 38ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Area The area inside one or more of the three...Ch. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Prob. 63ECh. 10.5 - Prob. 64ECh. 10.5 - Prob. 65ECh. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 69ECh. 10.5 - Prob. 70ECh. 10.5 - Prob. 71ECh. 10.5 - Prob. 72ECh. 10.5 - Prob. 73ECh. 10.5 - HOW DO YOU SEE IT? Which graph, traced out only...Ch. 10.5 - Prob. 75ECh. 10.5 - Surface Area of a Torus Find the surface area of...Ch. 10.5 - Approximating Area Consider the circle r=8cos. (a)...Ch. 10.5 - Prob. 78ECh. 10.5 - Prob. 79ECh. 10.5 - Logarithmic Spiral The curve represented by the...Ch. 10.5 - Prob. 81ECh. 10.5 - Area Find the area of the circle given by...Ch. 10.5 - Prob. 83ECh. 10.5 - Arc Length in Polar Form Use the formula for the...Ch. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Prob. 57ECh. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - Prob. 61ECh. 10.6 - Prob. 62ECh. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.6 - Prob. 68ECh. 10 - Matching In Exercises 1-6, match the equation with...Ch. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Identifying a Conic In Exercises 7-14, identify...Ch. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Finding the Standard Equation of a Parabola In...Ch. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Satellite Antenna A cross section of a large...Ch. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Using Parametric Equations In Exercises 27-34,...Ch. 10 - Prob. 30RECh. 10 - Using Parametric Equations In Exercises 27-34,...Ch. 10 - Prob. 32RECh. 10 - Using Parametric Equations In Exercises 27-34,...Ch. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Serpentine Curve Consider the parametric equations...Ch. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Horizontal and Vertical Tangency In Exercises...Ch. 10 - Prob. 50RECh. 10 - Horizontal and Vertical Tangency In Exerciser...Ch. 10 - Prob. 52RECh. 10 - Arc Length In Exercises S3 and 54, find the arc...Ch. 10 - Prob. 54RECh. 10 - Surface Area In Exercises 55 and 56, find the area...Ch. 10 - Prob. 56RECh. 10 - Area In Exercises 57 and 58, find the area of the...Ch. 10 - Prob. 58RECh. 10 - Polar-to-Rectangular Conversion In Exercises...Ch. 10 - Prob. 60RECh. 10 - Polar-to-Rectangular Conversion In Exercises...Ch. 10 - Prob. 62RECh. 10 - Rectangular-to-Polar Conversion In Exercises...Ch. 10 - Prob. 64RECh. 10 - Rectangular-to-Polar Conversion In Exercises...Ch. 10 - Prob. 66RECh. 10 - Rectangular-to-Polar Conversion In Exercises...Ch. 10 - Prob. 68RECh. 10 - Rectangular-to-Polar Conversion In Exercises...Ch. 10 - Prob. 70RECh. 10 - Rectangular-to-Polar Conversion In Exercises...Ch. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Polar-to-Rectangular Conversion In Exercises...Ch. 10 - Prob. 76RECh. 10 - Polar-to-Rectangular Conversion In Exercises...Ch. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Finding the Area of a Polar Region In Exercises...Ch. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 113RECh. 10 - Prob. 114RECh. 10 - Prob. 115RECh. 10 - Prob. 116RECh. 10 - Prob. 117RECh. 10 - Prob. 118RECh. 10 - Prob. 119RECh. 10 - Prob. 120RECh. 10 - Prob. 121RECh. 10 - Prob. 122RECh. 10 - Prob. 123RECh. 10 - Prob. 124RECh. 10 - Prob. 125RECh. 10 - Prob. 126RECh. 10 - Prob. 1PSCh. 10 - Prob. 2PSCh. 10 - Proof Prove Theorem 10.2, Reflective Property of a...Ch. 10 - Flight Paths An air traffic controller spots two...Ch. 10 - Strophoid The curve given by the parametric...Ch. 10 - Prob. 6PSCh. 10 - Prob. 7PSCh. 10 - Prob. 8PSCh. 10 - Prob. 9PSCh. 10 - Arc Length Consider the logarithmic spiral r=ea...Ch. 10 - Prob. 11PSCh. 10 - Prob. 12PSCh. 10 - Prob. 13PSCh. 10 - Prob. 14PSCh. 10 - Prob. 15PSCh. 10 - Prob. 16PSCh. 10 - Prob. 17PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- please solve with full steps pleasearrow_forward4. Identify at least two mistakes in Francisco's work. Correct the mistakes and complete the problem by using the second derivative test. 2f 2X 2. Find the relative maximum and relative minimum points of f(x) = 2x3 + 3x² - 3, using the First Derivative Test or the Second Derivative Test. bx+ bx 6x +6x=0 12x- af 24 = 0 x=0 108 -2 5. Identify at least three mistakes in Francisco's work. Then sketch the graph of the function and label the local max and local min. 1. Find the equation of the tangent line to the curve y=x-2x3+x-2 at the point (1.-2). Sketch the araph of y=x42x3+x-2 and the tangent line at (1,-2) y' = 4x-6x y' (1) = 4(1) - 667 - 2 = 4(-2)4127-6(-2) 5-8-19-20 =arrow_forward۳/۱ R2X2 2) slots per pole per phase = 3/31 B=18060 msl Ka, Sin (1) Kdl Isin ( sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 120*50 5) Synchronous speed, 120 x 50 S1000-950 1000 Copper losses 5kw 50105 Rotor input 5 0.05 loo kw 6) 1 1000rpm اذا ميريد شرح الكتب فقط Look = 7) rotov DC ined sove in peaper PU + 96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 3" 6" Σ=1 (2-1) π X9arrow_forward
- 1 R2 X2 2) slots per pole per phase = 3/31 B = 180 - 60 msl Kd Kol, Sin (no) Isin (6) 2 sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed; 120*50 Looo rem G S = 1000-950 solos 1000 Copper losses: 5kw Rotor input: 5 loo kw 0.05 1 اذا میرید شرح الكتب فقط look 7) rotor DC ined sove in pea PU+96er Q2// Find the volume of the solid bounded above by the cynnuer 2=6-x², on the sides by the cylinder x² + y² = 9, and below by the xy-plane. Q041 Convert 2 2x-2 Lake Gex 35 w2x-xབོ ,4-ཙཱཔ-y √4-x²-yz 21xy²dzdydx to(a) cylindrical coordinates, (b) Spherical coordinates. 201 25arrow_forwardshow full work pleasearrow_forward3. Describe the steps you would take to find the absolute max of the following function using Calculus f(x) = : , [-1,2]. Then use a graphing calculator to x-1 x²-x+1 approximate the absolute max in the closed interval.arrow_forward
- (7) (12 points) Let F(x, y, z) = (y, x+z cos yz, y cos yz). Ꮖ (a) (4 points) Show that V x F = 0. (b) (4 points) Find a potential f for the vector field F. (c) (4 points) Let S be a surface in R3 for which the Stokes' Theorem is valid. Use Stokes' Theorem to calculate the line integral Jos F.ds; as denotes the boundary of S. Explain your answer.arrow_forward(3) (16 points) Consider z = uv, u = x+y, v=x-y. (a) (4 points) Express z in the form z = fog where g: R² R² and f: R² → R. (b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate steps otherwise no credit. (c) (4 points) Let S be the surface parametrized by T(x, y) = (x, y, ƒ (g(x, y)) (x, y) = R². Give a parametric description of the tangent plane to S at the point p = T(x, y). (d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic approximation) of F = (fog) at a point (a, b). Verify that Q(x,y) F(a+x,b+y). =arrow_forward(6) (8 points) Change the order of integration and evaluate (z +4ry)drdy . So S√ ² 0arrow_forward
- (10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Find the solutions to a trig equation between 0 and 2pi; Author: Brian McLogan;https://www.youtube.com/watch?v=h7trDHjKCYc;License: Standard YouTube License, CC-BY