High School Math 2015 Common Core Algebra 2 Student Edition Grades 10/11
15th Edition
ISBN: 9780133281163
Author: Prentice Hall
Publisher: Prentice Hall
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 10.5, Problem 17PPSE
Solution
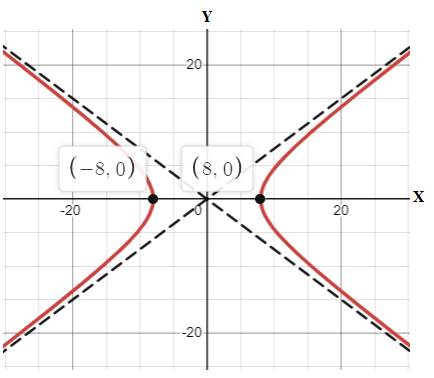
To find: The vertices, foci, and the asymptotes of the hyperbola x264−y236=1 . Also, sketch the graph.
The vertices of the hyperbola are (±8,0) , foci are (±10,0) and the asymptotes are y=±34x
Given information: The vertices equation of the hyperbola is x264−y236=1
Formula used: The equation of the hyperbola,
x2a2−y2b2=1 , here transverse axis is vertical.
Vertices of the hyperbola are (±a,0) and the foci are (±c,0) .
Here, c2=a2+b2
Slope of asymptotes are m=±ba , then asymptotes are y=±bax
Calculation:
Consider the equation of the hyperbola as,
x264−y236=1 ...... (1)
Compare equation (1) with x2a2−y2b2=1 , then
a2=64 implies that a=±8
And b2=36 implies that b=±6
Also, c2=a2+b2 implies that,
c2=64+36=100c=±10
Hence, the vertices of the hyperbola are (±a,0)=(±8,0) , foci are (±c,0)=(±10,0)
Also, the asymptotes are
y=±bax=±68x=±34x
The graph of the hyperbola can be drawn as,
Chapter 10 Solutions
High School Math 2015 Common Core Algebra 2 Student Edition Grades 10/11
Ch. 10.1 - Prob. 1LCCh. 10.1 - Prob. 2LCCh. 10.1 - Prob. 3LCCh. 10.1 - Prob. 4LCCh. 10.1 - Prob. 5LCCh. 10.1 - Prob. 6LCCh. 10.1 - Prob. 7PPSECh. 10.1 - Prob. 8PPSECh. 10.1 - Prob. 9PPSECh. 10.1 - Prob. 10PPSE
Ch. 10.1 - Prob. 11PPSECh. 10.1 - Prob. 12PPSECh. 10.1 - Prob. 13PPSECh. 10.1 - Prob. 14PPSECh. 10.1 - Prob. 15PPSECh. 10.1 - Prob. 16PPSECh. 10.1 - Prob. 17PPSECh. 10.1 - Prob. 18PPSECh. 10.1 - Prob. 19PPSECh. 10.1 - Prob. 20PPSECh. 10.1 - Prob. 21PPSECh. 10.1 - Prob. 22PPSECh. 10.1 - Prob. 23PPSECh. 10.1 - Prob. 24PPSECh. 10.1 - Prob. 25PPSECh. 10.1 - Prob. 26PPSECh. 10.1 - Prob. 27PPSECh. 10.1 - Prob. 28PPSECh. 10.1 - Prob. 29PPSECh. 10.1 - Prob. 30PPSECh. 10.1 - Prob. 31PPSECh. 10.1 - Prob. 32PPSECh. 10.1 - Prob. 33PPSECh. 10.1 - Prob. 34PPSECh. 10.1 - Prob. 35PPSECh. 10.1 - Prob. 36PPSECh. 10.1 - Prob. 37PPSECh. 10.1 - Prob. 38PPSECh. 10.1 - Prob. 39PPSECh. 10.1 - Prob. 40PPSECh. 10.1 - Prob. 41PPSECh. 10.1 - Prob. 42PPSECh. 10.1 - Prob. 43PPSECh. 10.1 - Prob. 44PPSECh. 10.1 - Prob. 45PPSECh. 10.1 - Prob. 46PPSECh. 10.1 - Prob. 47PPSECh. 10.1 - Prob. 48PPSECh. 10.1 - Prob. 49PPSECh. 10.1 - Prob. 50PPSECh. 10.1 - Prob. 51PPSECh. 10.1 - Prob. 52PPSECh. 10.1 - Prob. 53PPSECh. 10.1 - Prob. 54PPSECh. 10.1 - Prob. 55PPSECh. 10.1 - Prob. 56PPSECh. 10.1 - Prob. 57PPSECh. 10.1 - Prob. 58PPSECh. 10.1 - Prob. 59PPSECh. 10.1 - Prob. 60PPSECh. 10.1 - Prob. 61PPSECh. 10.1 - Prob. 62PPSECh. 10.1 - Prob. 63PPSECh. 10.1 - Prob. 64PPSECh. 10.1 - Prob. 65PPSECh. 10.1 - Prob. 66PPSECh. 10.1 - Prob. 67PPSECh. 10.1 - Prob. 68PPSECh. 10.1 - Prob. 69PPSECh. 10.1 - Prob. 1ECh. 10.1 - Prob. 2ECh. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10ECh. 10.1 - Prob. 11ECh. 10.1 - Prob. 12ECh. 10.2 - Prob. 1LCCh. 10.2 - Prob. 2LCCh. 10.2 - Prob. 3LCCh. 10.2 - Prob. 4LCCh. 10.2 - Prob. 5LCCh. 10.2 - Prob. 6LCCh. 10.2 - Prob. 7PPSECh. 10.2 - Prob. 8PPSECh. 10.2 - Prob. 9PPSECh. 10.2 - Prob. 10PPSECh. 10.2 - Prob. 11PPSECh. 10.2 - Prob. 12PPSECh. 10.2 - Prob. 13PPSECh. 10.2 - Prob. 14PPSECh. 10.2 - Prob. 15PPSECh. 10.2 - Prob. 16PPSECh. 10.2 - Prob. 17PPSECh. 10.2 - Prob. 18PPSECh. 10.2 - Prob. 19PPSECh. 10.2 - Prob. 20PPSECh. 10.2 - Prob. 21PPSECh. 10.2 - Prob. 22PPSECh. 10.2 - Prob. 23PPSECh. 10.2 - Prob. 24PPSECh. 10.2 - Prob. 25PPSECh. 10.2 - Prob. 26PPSECh. 10.2 - Prob. 27PPSECh. 10.2 - Prob. 28PPSECh. 10.2 - Prob. 29PPSECh. 10.2 - Prob. 30PPSECh. 10.2 - Prob. 31PPSECh. 10.2 - Prob. 32PPSECh. 10.2 - Prob. 33PPSECh. 10.2 - Prob. 34PPSECh. 10.2 - Prob. 35PPSECh. 10.2 - Prob. 36PPSECh. 10.2 - Prob. 37PPSECh. 10.2 - Prob. 38PPSECh. 10.2 - Prob. 39PPSECh. 10.2 - Prob. 40PPSECh. 10.2 - Prob. 41PPSECh. 10.2 - Prob. 42PPSECh. 10.2 - Prob. 43PPSECh. 10.2 - Prob. 44PPSECh. 10.2 - Prob. 45PPSECh. 10.2 - Prob. 46PPSECh. 10.2 - Prob. 47PPSECh. 10.2 - Prob. 48PPSECh. 10.2 - Prob. 49PPSECh. 10.2 - Prob. 50PPSECh. 10.2 - Prob. 51PPSECh. 10.2 - Prob. 52PPSECh. 10.2 - Prob. 53PPSECh. 10.2 - Prob. 54PPSECh. 10.2 - Prob. 55PPSECh. 10.2 - Prob. 56PPSECh. 10.2 - Prob. 57PPSECh. 10.2 - Prob. 58PPSECh. 10.2 - Prob. 59PPSECh. 10.2 - Prob. 60PPSECh. 10.2 - Prob. 61PPSECh. 10.2 - Prob. 62PPSECh. 10.2 - Prob. 63PPSECh. 10.2 - Prob. 64PPSECh. 10.2 - Prob. 65PPSECh. 10.2 - Prob. 66PPSECh. 10.2 - Prob. 67PPSECh. 10.2 - Prob. 68PPSECh. 10.2 - Prob. 69PPSECh. 10.3 - Prob. 1LCCh. 10.3 - Prob. 2LCCh. 10.3 - Prob. 3LCCh. 10.3 - Prob. 4LCCh. 10.3 - Prob. 5LCCh. 10.3 - Prob. 6LCCh. 10.3 - Prob. 7PPSECh. 10.3 - Prob. 8PPSECh. 10.3 - Prob. 9PPSECh. 10.3 - Prob. 10PPSECh. 10.3 - Prob. 11PPSECh. 10.3 - Prob. 12PPSECh. 10.3 - Prob. 13PPSECh. 10.3 - Prob. 14PPSECh. 10.3 - Prob. 15PPSECh. 10.3 - Prob. 16PPSECh. 10.3 - Prob. 17PPSECh. 10.3 - Prob. 18PPSECh. 10.3 - Prob. 19PPSECh. 10.3 - Prob. 20PPSECh. 10.3 - Prob. 21PPSECh. 10.3 - Prob. 22PPSECh. 10.3 - Prob. 23PPSECh. 10.3 - Prob. 24PPSECh. 10.3 - Prob. 25PPSECh. 10.3 - Prob. 26PPSECh. 10.3 - Prob. 27PPSECh. 10.3 - Prob. 28PPSECh. 10.3 - Prob. 29PPSECh. 10.3 - Prob. 30PPSECh. 10.3 - Prob. 31PPSECh. 10.3 - Prob. 32PPSECh. 10.3 - Prob. 33PPSECh. 10.3 - Prob. 34PPSECh. 10.3 - Prob. 35PPSECh. 10.3 - Prob. 36PPSECh. 10.3 - Prob. 37PPSECh. 10.3 - Prob. 38PPSECh. 10.3 - Prob. 39PPSECh. 10.3 - Prob. 40PPSECh. 10.3 - Prob. 41PPSECh. 10.3 - Prob. 42PPSECh. 10.3 - Prob. 43PPSECh. 10.3 - Prob. 44PPSECh. 10.3 - Prob. 45PPSECh. 10.3 - Prob. 46PPSECh. 10.3 - Prob. 47PPSECh. 10.3 - Prob. 48PPSECh. 10.3 - Prob. 49PPSECh. 10.3 - Prob. 50PPSECh. 10.3 - Prob. 51PPSECh. 10.3 - Prob. 52PPSECh. 10.3 - Prob. 53PPSECh. 10.3 - Prob. 54PPSECh. 10.3 - Prob. 55PPSECh. 10.3 - Prob. 56PPSECh. 10.3 - Prob. 57PPSECh. 10.3 - Prob. 58PPSECh. 10.3 - Prob. 59PPSECh. 10.3 - Prob. 60PPSECh. 10.3 - Prob. 61PPSECh. 10.3 - Prob. 62PPSECh. 10.3 - Prob. 63PPSECh. 10.3 - Prob. 64PPSECh. 10.3 - Prob. 65PPSECh. 10.3 - Prob. 66PPSECh. 10.4 - Prob. 1LCCh. 10.4 - Prob. 2LCCh. 10.4 - Prob. 3LCCh. 10.4 - Prob. 4LCCh. 10.4 - Prob. 5LCCh. 10.4 - Prob. 6LCCh. 10.4 - Prob. 7PPSECh. 10.4 - Prob. 8PPSECh. 10.4 - Prob. 9PPSECh. 10.4 - Prob. 10PPSECh. 10.4 - Prob. 11PPSECh. 10.4 - Prob. 12PPSECh. 10.4 - Prob. 13PPSECh. 10.4 - Prob. 14PPSECh. 10.4 - Prob. 15PPSECh. 10.4 - Prob. 16PPSECh. 10.4 - Prob. 17PPSECh. 10.4 - Prob. 18PPSECh. 10.4 - Prob. 19PPSECh. 10.4 - Prob. 20PPSECh. 10.4 - Prob. 21PPSECh. 10.4 - Prob. 22PPSECh. 10.4 - Prob. 23PPSECh. 10.4 - Prob. 24PPSECh. 10.4 - Prob. 25PPSECh. 10.4 - Prob. 26PPSECh. 10.4 - Prob. 27PPSECh. 10.4 - Prob. 28PPSECh. 10.4 - Prob. 29PPSECh. 10.4 - Prob. 30PPSECh. 10.4 - Prob. 31PPSECh. 10.4 - Prob. 32PPSECh. 10.4 - Prob. 33PPSECh. 10.4 - Prob. 34PPSECh. 10.4 - Prob. 36PPSECh. 10.4 - Prob. 37PPSECh. 10.4 - Prob. 38PPSECh. 10.4 - Prob. 39PPSECh. 10.4 - Prob. 40PPSECh. 10.4 - Prob. 41PPSECh. 10.4 - Prob. 44PPSECh. 10.4 - Prob. 45PPSECh. 10.4 - Prob. 46PPSECh. 10.4 - Prob. 48PPSECh. 10.4 - Prob. 49PPSECh. 10.4 - Prob. 50PPSECh. 10.4 - Prob. 51PPSECh. 10.4 - Prob. 52PPSECh. 10.4 - Prob. 53PPSECh. 10.4 - Prob. 54PPSECh. 10.4 - Prob. 55PPSECh. 10.4 - Prob. 56PPSECh. 10.4 - Prob. 57PPSECh. 10.4 - Prob. 58PPSECh. 10.4 - Prob. 59PPSECh. 10.5 - Prob. 1LCCh. 10.5 - Prob. 2LCCh. 10.5 - Prob. 3LCCh. 10.5 - Prob. 4LCCh. 10.5 - Prob. 5LCCh. 10.5 - Prob. 6LCCh. 10.5 - Prob. 7LCCh. 10.5 - Prob. 8PPSECh. 10.5 - Prob. 9PPSECh. 10.5 - Prob. 10PPSECh. 10.5 - Prob. 11PPSECh. 10.5 - Prob. 12PPSECh. 10.5 - Prob. 13PPSECh. 10.5 - Prob. 14PPSECh. 10.5 - Prob. 15PPSECh. 10.5 - Prob. 16PPSECh. 10.5 - Prob. 17PPSECh. 10.5 - Prob. 18PPSECh. 10.5 - Prob. 19PPSECh. 10.5 - Prob. 20PPSECh. 10.5 - Prob. 21PPSECh. 10.5 - Prob. 22PPSECh. 10.5 - Prob. 23PPSECh. 10.5 - Prob. 24PPSECh. 10.5 - Prob. 25PPSECh. 10.5 - Prob. 26PPSECh. 10.5 - Prob. 27PPSECh. 10.5 - Prob. 28PPSECh. 10.5 - Prob. 29PPSECh. 10.5 - Prob. 30PPSECh. 10.5 - Prob. 31PPSECh. 10.5 - Prob. 32PPSECh. 10.5 - Prob. 33PPSECh. 10.5 - Prob. 34PPSECh. 10.5 - Prob. 35PPSECh. 10.5 - Prob. 36PPSECh. 10.5 - Prob. 37PPSECh. 10.5 - Prob. 38PPSECh. 10.5 - Prob. 39PPSECh. 10.5 - Prob. 40PPSECh. 10.5 - Prob. 41PPSECh. 10.5 - Prob. 42PPSECh. 10.6 - Prob. 1LCCh. 10.6 - Prob. 2LCCh. 10.6 - Prob. 3LCCh. 10.6 - Prob. 4LCCh. 10.6 - Prob. 5LCCh. 10.6 - Prob. 6LCCh. 10.6 - Prob. 7LCCh. 10.6 - Prob. 8PPSECh. 10.6 - Prob. 9PPSECh. 10.6 - Prob. 10PPSECh. 10.6 - Prob. 11PPSECh. 10.6 - Prob. 12PPSECh. 10.6 - Prob. 13PPSECh. 10.6 - Prob. 14PPSECh. 10.6 - Prob. 15PPSECh. 10.6 - Prob. 16PPSECh. 10.6 - Prob. 17PPSECh. 10.6 - Prob. 18PPSECh. 10.6 - Prob. 19PPSECh. 10.6 - Prob. 20PPSECh. 10.6 - Prob. 21PPSECh. 10.6 - Prob. 22PPSECh. 10.6 - Prob. 23PPSECh. 10.6 - Prob. 24PPSECh. 10.6 - Prob. 25PPSECh. 10.6 - Prob. 26PPSECh. 10.6 - Prob. 27PPSECh. 10.6 - Prob. 28PPSECh. 10.6 - Prob. 29PPSECh. 10.6 - Prob. 30PPSECh. 10.6 - Prob. 31PPSECh. 10.6 - Prob. 32PPSECh. 10.6 - Prob. 33PPSECh. 10.6 - Prob. 34PPSECh. 10.6 - Prob. 35PPSECh. 10.6 - Prob. 36PPSECh. 10.6 - Prob. 37PPSECh. 10.6 - Prob. 38PPSECh. 10.6 - Prob. 39PPSECh. 10.6 - Prob. 40PPSECh. 10.6 - Prob. 41PPSECh. 10.6 - Prob. 42PPSECh. 10.6 - Prob. 43PPSECh. 10.6 - Prob. 44PPSECh. 10.6 - Prob. 45PPSECh. 10.6 - Prob. 46PPSECh. 10.6 - Prob. 47PPSECh. 10.6 - Prob. 48PPSECh. 10.6 - Prob. 49PPSECh. 10.6 - Prob. 50PPSECh. 10.6 - Prob. 51PPSECh. 10.6 - Prob. 52PPSECh. 10.6 - Prob. 53PPSECh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10 - Prob. 1GRCh. 10 - Prob. 2GRCh. 10 - Prob. 3GRCh. 10 - Prob. 4GRCh. 10 - Prob. 5GRCh. 10 - Prob. 6GRCh. 10 - Prob. 7GRCh. 10 - Prob. 8GRCh. 10 - Prob. 9GRCh. 10 - Prob. 10GRCh. 10 - Prob. 11GRCh. 10 - Prob. 12GRCh. 10 - Prob. 13GRCh. 10 - Prob. 14GRCh. 10 - Prob. 15GRCh. 10 - Prob. 16GRCh. 10 - Prob. 17GRCh. 10 - Prob. 18GRCh. 10 - Prob. 19GRCh. 10 - Prob. 20GRCh. 10 - Prob. 21GRCh. 10 - Prob. 22GRCh. 10 - Prob. 1MCQCh. 10 - Prob. 2MCQCh. 10 - Prob. 3MCQCh. 10 - Prob. 4MCQCh. 10 - Prob. 5MCQCh. 10 - Prob. 6MCQCh. 10 - Prob. 7MCQCh. 10 - Prob. 8MCQCh. 10 - Prob. 9MCQCh. 10 - Prob. 10MCQCh. 10 - Prob. 11MCQCh. 10 - Prob. 12MCQCh. 10 - Prob. 13MCQCh. 10 - Prob. 14MCQCh. 10 - Prob. 15MCQCh. 10 - Prob. 16MCQCh. 10 - Prob. 17MCQCh. 10 - Prob. 18MCQCh. 10 - Prob. 19MCQCh. 10 - Prob. 20MCQCh. 10 - Prob. 21MCQCh. 10 - Prob. 22MCQCh. 10 - Prob. 23MCQCh. 10 - Prob. 24MCQCh. 10 - Prob. 25MCQCh. 10 - Prob. 26MCQCh. 10 - Prob. 27MCQCh. 10 - Prob. 1CVCh. 10 - Prob. 2CVCh. 10 - Prob. 3CVCh. 10 - Prob. 4CVCh. 10 - Prob. 5CVCh. 10 - Prob. 6ECh. 10 - Prob. 7ECh. 10 - Prob. 8ECh. 10 - Prob. 9ECh. 10 - Prob. 10ECh. 10 - Prob. 11ECh. 10 - Prob. 12ECh. 10 - Prob. 13ECh. 10 - Prob. 14ECh. 10 - Prob. 15ECh. 10 - Prob. 16ECh. 10 - Prob. 17ECh. 10 - Prob. 18ECh. 10 - Prob. 19ECh. 10 - Prob. 20ECh. 10 - Prob. 21ECh. 10 - Prob. 22ECh. 10 - Prob. 23ECh. 10 - Prob. 24ECh. 10 - Prob. 25ECh. 10 - Prob. 26ECh. 10 - Prob. 27ECh. 10 - Prob. 28ECh. 10 - Prob. 29ECh. 10 - Prob. 30ECh. 10 - Prob. 31ECh. 10 - Prob. 32ECh. 10 - Prob. 33ECh. 10 - Prob. 34ECh. 10 - Prob. 35ECh. 10 - Prob. 36ECh. 10 - Prob. 37ECh. 10 - Prob. 38ECh. 10 - Prob. 39ECh. 10 - Prob. 40ECh. 10 - Prob. 41ECh. 10 - Prob. 42ECh. 10 - Prob. 43ECh. 10 - Prob. 44ECh. 10 - Prob. 45ECh. 10 - Prob. 1CTCh. 10 - Prob. 2CTCh. 10 - Prob. 3CTCh. 10 - Prob. 4CTCh. 10 - Prob. 5CTCh. 10 - Prob. 6CTCh. 10 - Prob. 7CTCh. 10 - Prob. 8CTCh. 10 - Prob. 9CTCh. 10 - Prob. 10CTCh. 10 - Prob. 11CTCh. 10 - Prob. 12CTCh. 10 - Prob. 13CTCh. 10 - Prob. 14CTCh. 10 - Prob. 15CTCh. 10 - Prob. 16CTCh. 10 - Prob. 17CTCh. 10 - Prob. 18CTCh. 10 - Prob. 19CTCh. 10 - Prob. 20CTCh. 10 - Prob. 21CTCh. 10 - Prob. 22CTCh. 10 - Prob. 23CTCh. 10 - Prob. 24CTCh. 10 - Prob. 25CTCh. 10 - Prob. 26CTCh. 10 - Prob. 27CTCh. 10 - Prob. 28CTCh. 10 - Prob. 29CTCh. 10 - Prob. 30CTCh. 10 - Prob. 31CTCh. 10 - Prob. 32CTCh. 10 - Prob. 1CCSRCh. 10 - Prob. 2CCSRCh. 10 - Prob. 3CCSRCh. 10 - Prob. 4CCSRCh. 10 - Prob. 5CCSRCh. 10 - Prob. 6CCSRCh. 10 - Prob. 7CCSRCh. 10 - Prob. 8CCSRCh. 10 - Prob. 9CCSRCh. 10 - Prob. 10CCSRCh. 10 - Prob. 11CCSRCh. 10 - Prob. 12CCSRCh. 10 - Prob. 13CCSRCh. 10 - Prob. 14CCSRCh. 10 - Prob. 15CCSRCh. 10 - Prob. 16CCSRCh. 10 - Prob. 17CCSRCh. 10 - Prob. 18CCSRCh. 10 - Prob. 19CCSRCh. 10 - Prob. 20CCSRCh. 10 - Prob. 21CCSRCh. 10 - Prob. 22CCSRCh. 10 - Prob. 23CCSRCh. 10 - Prob. 24CCSRCh. 10 - Prob. 25CCSRCh. 10 - Prob. 26CCSR
Knowledge Booster
Similar questions
- Jason has a bag that contains 8 identically shaped boxes. 6 of the boxes are blue, and 2 are green. 3 of the blue boxes have a prize, and 1 of the green boxes has a prize. Jason randomly selects a box from the bag. Let A be the event that he selects a box with a prize and B be the event that the box is green. Which of the following statements are true? Choose all answers that apply: [^] P(A|B) = P(A), the conditional probability that Jason selects a box with a prize given that he has chosen a green box is equal to the probability that Jason selects a box with a prize. B P(B|A) = P(B), the conditional probability that Jason selects a green box given that he has chosen a box with a prize is equal to the probability that Jason selects a green box. Events A and B are independent events. The outcomes of events A and B are dependent on each other. E P(A and B) = P(A) · P(B), the probability that Jason selects a box that contains a prize and is green is equal to the probability that Jason…arrow_forward4) A researcher gathered data on the amount of time students spent studying per week. Given the following frequency distribution, fill in the relative and cumulative frequency. Hours per week: at least Frequency Relative Frequency Cumulative Relative Frequency 0 but less than 2 4 2 but less than 4 15 4 but less than 6 41 6 but less than 8 20 8 but less than 10 7 10 or more 3 a) What percentage of students study less than 6 hours per week?arrow_forwardoptions are greater than less than or about the same asarrow_forward
- A candy machine contains over \[1{,}000\] pieces of candy, \[30\%\] of which are blue. Customers get an SRS of \[15\] candies in a purchase. Let \[X=\] the number of blue candies that a random customer gets in a purchase. Find the mean and standard deviation of \[X\].You may round your answers to the nearest tenth.arrow_forwardA television show tests the abilities of alleged psychics by presenting contestants with a set of \[4\] cards placed upside down, \[1\] of which has a star printed on it. Each contestant attempts to identify which card has the star on it for a series of \[50\] trials. Assuming that the contestants are purely guessing, what are the mean and standard deviation of the number of trials where the contestant guesses correctly?You may round your answers to the nearest tenth.arrow_forwardA television show tests the abilities of alleged psychics by presenting contestants with a set of \[4\] cards placed upside down, \[1\] of which has a star printed on it. Each contestant attempts to identify which card has the star on it for a series of \[50\] trials. Assuming that the contestants are purely guessing, what are the mean and standard deviation of the number of trials where the contestant guesses correctly?You may round your answers to the nearest tenth.arrow_forward
- A large fast-food chain runs a promotion where \[1\]-in-\[4\] boxes of french fries include a coupon for a free box of french fries. Suppose that some location sells \[100\] of these boxes of fries per day. Let \[X=\] the number of coupons won per day. Find the mean and standard deviation of \[X\].You may round your answers to the nearest tenth.arrow_forwardA roulette wheel has \[38\] slots, of which \[18\] are red, \[18\] are black, and \[2\] are green. In each round of the game, a ball is tossed in the spinning wheel and lands in a random slot. Suppose we watch \[7\] rounds of this game, and let \[R\] represent the number of rounds where the ball lands in a red slot. Which of the following would find \[P(R=3)\]?arrow_forwardA small college has 800students, 10% of which are left-handed. Suppose they take an SRS of 8students. Let [L=] the number of left-handed students in the sample. Which of the following would find [P(L=2)]?arrow_forward
- [2 01 3. (12 pts) Let A = 1 1 and b = 1 L2 1] 213 [2] (1) (2) Use the Gram-Schmidt process to find an orthonormal basis for the column space of A. Factor A into a product QR, where Q has an orthonormal set of column vectors and R is upper triangular. (3) Solve the least squares problem Ax = b.arrow_forward22.) Mr. Vedrani has a pool with a deck built around it. The equation (2x+14)(2x+19) = 650 represents the relationship of the side lengths (in feet) of the entire pool area (in square feet). a.) If 350 represents the area of the pool and deck area, what do the expressions (2x+14) and (2x+19) each represent? b.) Using graphing technology, find x, the width of the deck around the pool. If necessary, round to the nearest tenth. x=arrow_forwardHow do I get common factors?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education